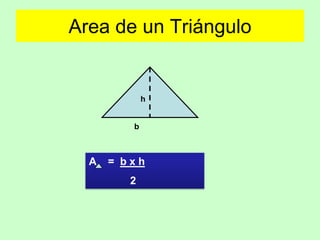
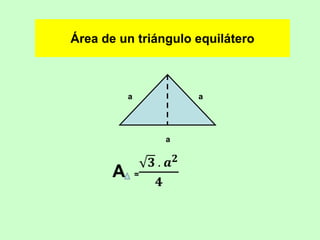
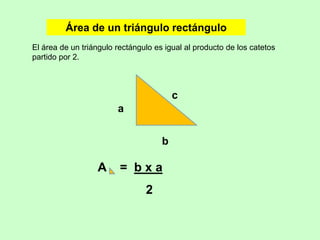
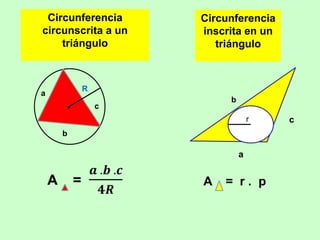
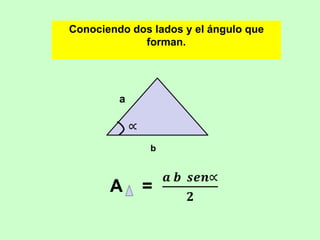
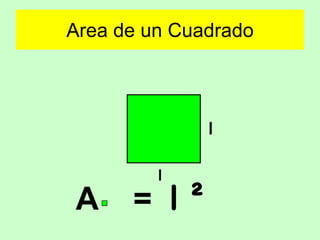
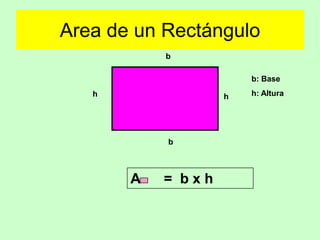
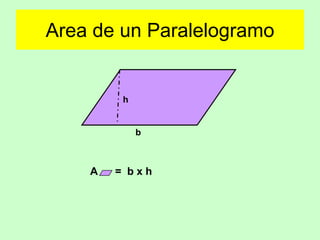
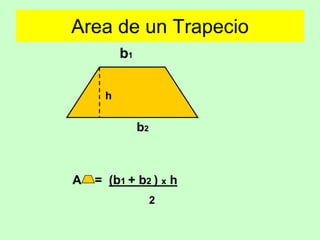
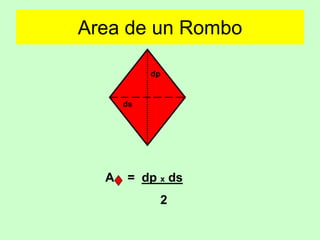
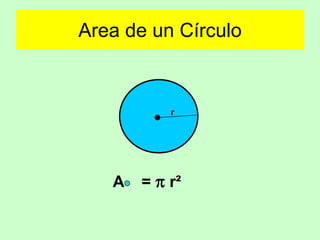
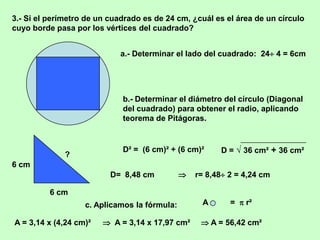
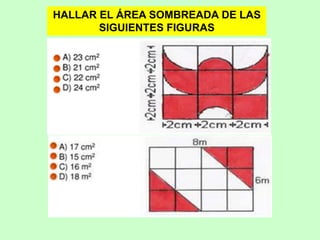
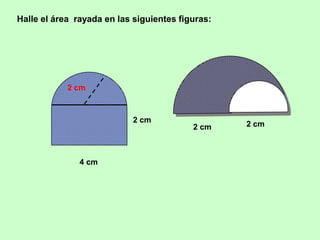
Este documento presenta fórmulas para calcular el área de diferentes figuras geométricas planas, incluyendo triángulos, cuadrados, rectángulos, trapecios, rombos, círculos y polígonos regulares. También incluye ejemplos numéricos para practicar el cálculo del área.

1. Áreas de Regiones Poligonales

2. Area de un Triángulo
h
b
A = bxh
2

3. Área de un triángulo equilátero
a a
a

4. Área de un triángulo rectángulo
El área de un triángulo rectángulo es igual al producto de los catetos
partido por 2.
c
a
b
A = bxa
2

5. Fórmula de Herón El semiperímetro de un
triángulo es igual a la
suma de sus lados partido
La fórmula de Herón se por 2.
utiliza para hallar el área de Se nombra con la letra p.
un triángulo conociendo
sus tres lados.
a b
c

6. Circunferencia Circunferencia
circunscrita a un inscrita en un
triángulo triángulo
R
a
b
c
r c
b
a
A = r. p

7. Conociendo dos lados y el ángulo que
forman.
a
b

8. Area de un Cuadrado
l
l
A = l²

9. Area de un Rectángulo
b
b: Base
h h h: Altura
b
A = bxh

10. Area de un Paralelogramo
h
b
A = bxh

11. Area de un Trapecio
b1
h
b2
A = (b1 + b2 ) x h
2

12. Area de un Rombo
dp
ds
A = dp x ds
2

13. Area de un Círculo
r
A =  r²

14. Area de un Polígono Regular
a: Apotema
a
El área de un polígono regular es igual a la mitad del producto de su
perímetro por la apotema.
A = Pxa
2

15. Ejercicios
1.- Un terreno cuadrado tiene 516
metros de perímetro. ¿cuál es su
área?
P = 516 metros. Como es un cuadrado, dividimos entre 4 para hallar la
medida de los lados.
516  4 = 129 metros. Cada lado mide 129 metros
A =  A = (129 m)²  A = 16.641 m²
l²

16. 2.- La base de un rectángulo es de
24 cm y su altura es ¾ de su base.
¿Cuál es su área?
a.- Determinamos la altura (h)
¾ x 24 = 72/4 = 18 cm
b.- Aplicamos la fórmula:
A = bxh
A = 432 cm²
= 24 cm x 18 cm =

17. 3.- Si el perímetro de un cuadrado es de 24 cm, ¿cuál es el área de un círculo
cuyo borde pasa por los vértices del cuadrado?
a.- Determinar el lado del cuadrado: 24 4 = 6cm
b.- Determinar el diámetro del círculo (Diagonal
del cuadrado) para obtener el radio, aplicando
teorema de Pitágoras.
D² = (6 cm)² + (6 cm)² D = √ 36 cm² + 36 cm²
?
6 cm
D= 8,48 cm  r= 8,48 2 = 4,24 cm
6 cm
c. Aplicamos la fórmula: A =  r²
A = 3,14 x (4,24 cm)²  A = 3,14 x 17,97 cm²  A = 56,42 cm²

18. HALLAR EL ÁREA SOMBREADA DE LAS
SIGUIENTES FIGURAS

19. Halle el área rayada en las siguientes figuras:
2 cm
2 cm
2 cm 2 cm
4 cm