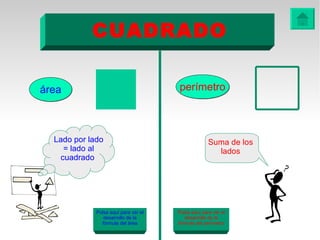
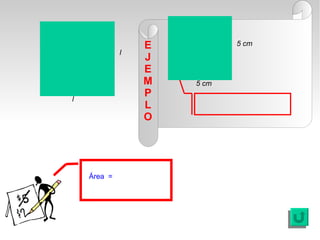
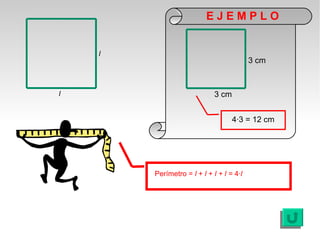
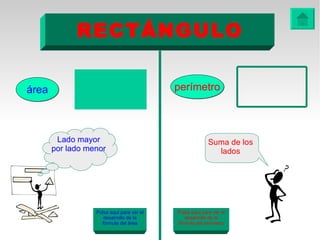
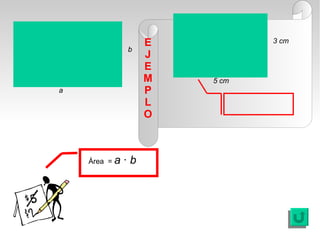
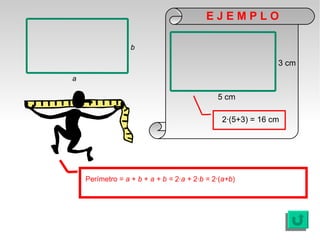
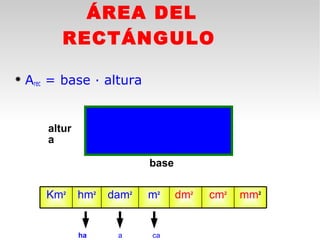
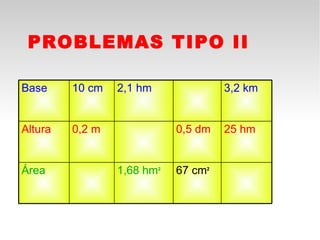
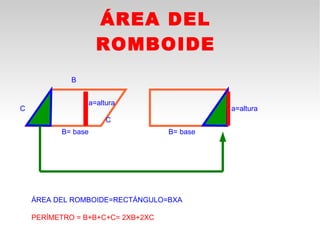
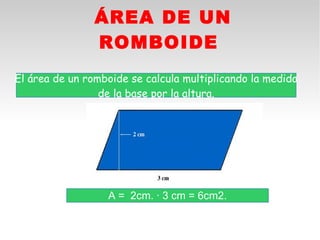
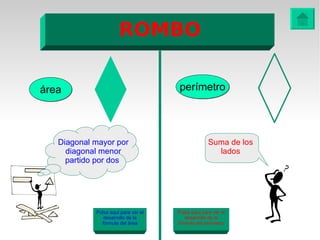
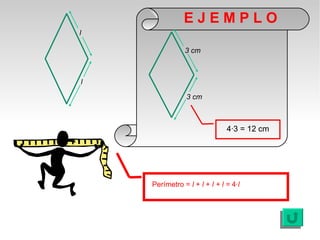
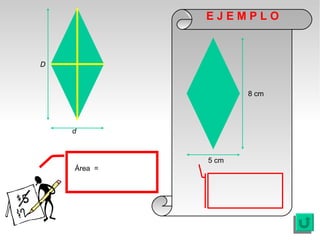
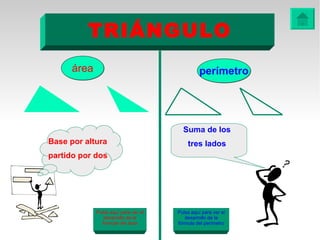
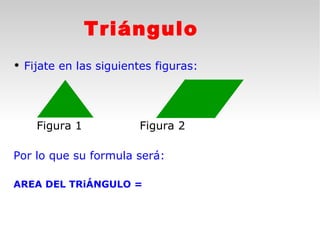
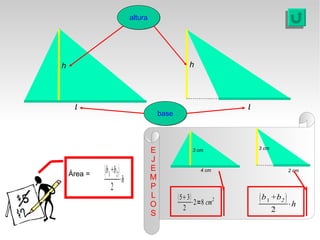
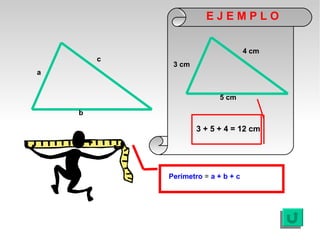
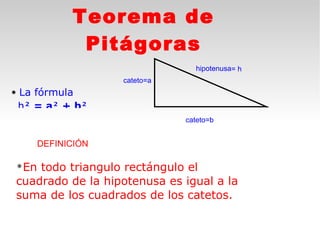
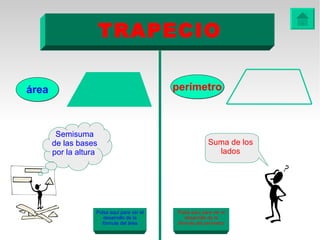
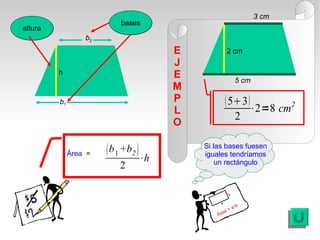
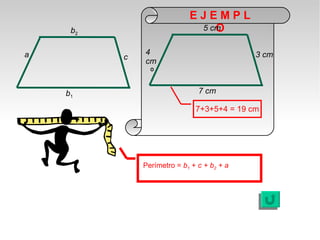
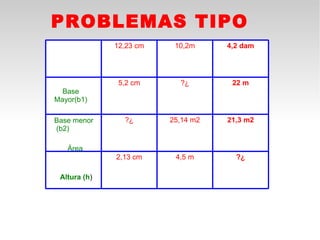
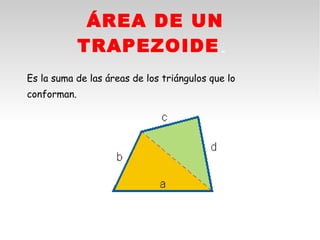
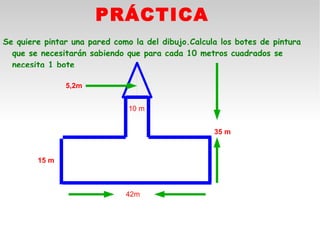
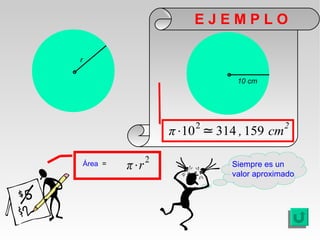
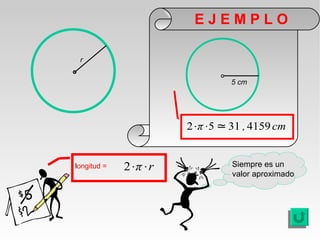
Este documento presenta fórmulas y ejemplos para calcular el área y perímetro de varias figuras geométricas planas, incluyendo cuadrados, rectángulos, rombos, triángulos, trapecios, polígonos regulares y círculos. Explica cómo calcular el área multiplicando las medidas apropiadas y el perímetro sumando los lados. También incluye ejercicios prácticos para que los estudiantes apliquen estas fórmulas geométricas básicas.

1. MATEMÁTICAS
ÁREAS Y PERÍMETROS DE
FIGURAS PLANAS
EJERCICIOS PRÁCTICOS
C.E.I.P. ”Martín Noguera”.
Jaén Edu Becerra 2009-10

2. CUADRADO
área perímetro
Lado por lado Suma de los
= lado al lados
cuadrado
Pulsa aquí para ver el Pulsa aquí para ver el
desarrollo de la desarrollo de la
fórmula del área fórmula del perímetro

3. E 5 cm
l
J
E
M 5 cm
l
P
L
O
Área =

4. EJEMPLO
l
3 cm
l 3 cm
4·3 = 12 cm
Perímetro = l + l + l + l = 4·l

5. Dado el Perímetro
Calcular
el Área
ÁREA DEL CUADRADO =
A =LxL = L2
Calcula el área de un cuadrado de 32 m. de perímetro.

6. Dada el Área Calcular
el Lado
Calcula cuánto tiene que medir el lado de un
cuadrado para que su área sea:
a) 81 m²
b) 3600 km²
c) 144 mm²

7. RECTÁNGULO
área perímetro
Lado mayor Suma de los
por lado menor lados
Pulsa aquí para ver el Pulsa aquí para ver el
desarrollo de la desarrollo de la
fórmula del área fórmula del perímetro

8. E 3 cm
b
J
E
M 5 cm
a P
L
O
Área = a ·b

9. EJEMPLO
b
3 cm
a
5 cm
2·(5+3) = 16 cm
Perímetro = a + b + a + b = 2·a + 2·b = 2·(a+b)

10. ÁREA DEL
RECTÁNGULO
 Arec = base · altura
altur
a
base
Km2 hm2 dam2 m2 dm2 cm2 mm2
ha a ca

11. PROBLEMAS TIPO
Calcula el área de los siguientes rectángulos:
a) Base: 12 m Altura: 20 m
b) Base: 2 km Altura: 1425 m
Queremos construir una nave, con forma rectangular,
de 42 m². Si mide 7 m de largo ¿cuánto ha de ser
el ancho?

12. PROBLEMAS TIPO II
Base 10 cm 2,1 hm 3,2 km
Altura 0,2 m 0,5 dm 25 hm
Área 1,68 hm2 67 cm2

13. ÁREA DEL
ROMBOIDE
B
a=altura
C a=altura
C
B= base B= base
ÁREA DEL ROMBOIDE=RECTÁNGULO=BXA
PERÍMETRO = B+B+C+C= 2XB+2XC

14. ÁREA DE UN
ROMBOIDE
El área de un romboide se calcula multiplicando la medida
de la base por la altura.
A = 2cm. · 3 cm = 6cm2.

15. ROMBO
área perímetro
Diagonal mayor por Suma de los
diagonal menor lados
partido por dos
Pulsa aquí para ver el Pulsa aquí para ver el
desarrollo de la desarrollo de la
fórmula del área fórmula del perímetro

16. EJEMPLO
l
3 cm
l
3 cm
4·3 = 12 cm
Perímetro = l + l + l + l = 4·l

17. EJEMPLO
D
8 cm
d
5 cm
Área =

18. PROBLEMAS TIPO
AREA DEL ROMBO=
Las diagonales de un rombo miden 42 cm y 2 dm
respectivamente. Calcula su área.
Queremos construir un rombo de 24,6 cm² de área. Si una de
las diagonales mide 0,6 dm. ¿cuánto tienen que medir la
otra?

19. TRIÁNGULO
área perímetro
Suma de los
Base por altura tres lados
partido por dos
Pulsa aquí para ver el Pulsa aquí para ver el
desarrollo de la desarrollo de la
fórmula del área fórmula del perímetro

20. Triángulo
 Fijate en las siguientes figuras:
Figura 1 Figura 2
Por lo que su formula será:
AREA DEL TRiÁNGULO =

21. altura
h h
b b
base
E 3 cm 3 cm
J
Área = b1 +b2  E
M
4 cm 2 cm
⋅h
2 P
L  53   b 1 +b2 
O ⋅2=8 cm2 ⋅h
2 2
S

22. EJEMPLO
4 cm
c
3 cm
a
5 cm
b
3 + 5 + 4 = 12 cm
Perímetro = a + b + c

23. Teorema de
Pitágoras
hipotenusa= h
cateto=a
 La fórmula
h² = a² + b²
cateto=b
DEFINICIÓN
En todo triangulo rectángulo el
cuadrado de la hipotenusa es igual a la
suma de los cuadrados de los catetos.

24. PROBLEMAS TIPO
Base 12,3m 6m 7,25m 42 cm
Altura 6m 2,4 m 210 mm
Área 18dm2
Una escalera esta apoyada en la pared. Sabiendo que la distancia del suelo
a la parte más alta de la escaleta es de 5m y la de la pared a la parte baja es de
3 m :¿Cuánto mide la escalera?
¿?
5m
3m

25. TRAPECIO
área perímetro
Semisuma
de las bases Suma de los
por la altura lados
Pulsa aquí para ver el Pulsa aquí para ver el
desarrollo de la desarrollo de la
fórmula del área fórmula del perímetro

26. 3 cm
bases
altura
b2
E 2 cm
J
h E 5 cm
M
b1 P  53 
L ⋅2=8 cm2
2
O
Si las bases fuesen
Área =  b 1 +b2  iguales tendríamos
⋅h un rectángulo
2
b
a
a ·b
a=
Áre

27. EJEMPL
b2 O
5 cm
a 4 3 cm
c
cm
º
b1 7 cm
7+3+5+4 = 19 cm
Perímetro = b1 + c + b2 + a

28. PROBLEMAS TIPO
12,23 cm 10,2m 4,2 dam
5,2 cm ?¿ 22 m
Base
Mayor(b1)
Base menor ?¿ 25,14 m2 21,3 m2
(b2)
Área
2,13 cm 4,5 m ?¿
Altura (h)

29. ÁREA DE UN
TRAPEZOIDE.
Es la suma de las áreas de los triángulos que lo
conforman.

30. PRÁCTICA
Se quiere pintar una pared como la del dibujo.Calcula los botes de pintura
que se necesitarán sabiendo que para cada 10 metros cuadrados se
necesita 1 bote
5,2m
10 m
35 m
15 m
42m

31. ÁREA DE UN POLÍGONO
REGULAR
El Área de un polígono regular es igual al perímetro por la apotema
Partido por dos
Apotema Segmento que une el centro del poligono con la mitad del lado
Perímetro es el nº de lados por el valor del lado.
Perímetro =Lado x Nº de lados.
A=P·a·
2

32. PRÁCTICA
1.- Halla el área de un hexágono de 32,5 dm de perimetro y cuya
apotema mide 28 cm
2.- Halla el área de un pentágono cuyo lado es 2,5 m y su
apotema 1,25m

33. CIRCUNFERENCIA Y
CÍRCULO
círculo circunferencia
π (pi) por el
radio al
cuadrado Diámetro por π
π ≅ 3,14159...
Pulsa aquí para ver el Pulsa aquí para ver el
desarrollo de la desarrollo de la
fórmula del área fórmula del perímetro

34. EJEMPLO
r
10 cm
2 2
π⋅10 ≃ 314 , 159 cm
2
Área = π⋅r Siempre es un
valor aproximado

35. EJEMPLO
r
5 cm
2⋅π⋅5 ≃ 31 , 4159 cm
longitud = 2⋅π⋅r Siempre es un
valor aproximado