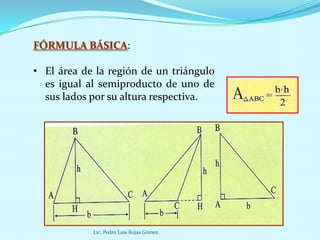
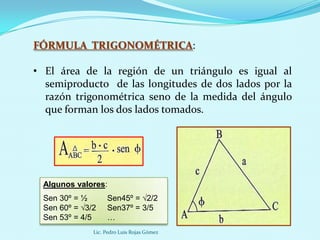
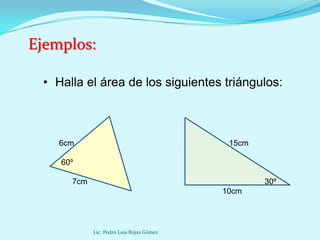
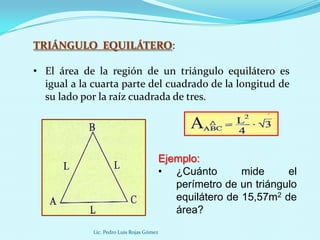
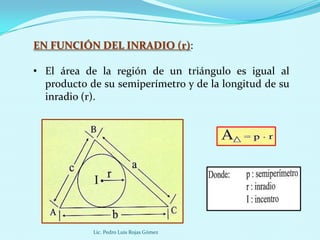
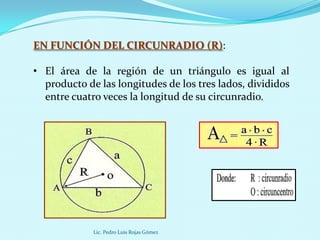
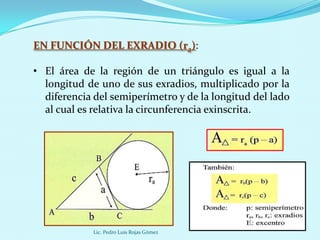
Este documento presenta diferentes fórmulas para calcular el área de regiones triangulares, cuadriláteras y circulares. Explica las fórmulas básicas, de Herón, trigonométrica y para triángulos equiláteros para calcular el área de triángulos. También cubre cálculos de área basados en el inradio, circunradio y exradio. Finalmente, incluye ejemplos prácticos.

1. UNIDAD II:
Lic. Pedro Luis Rojas Gómez

2. TEMAS A TRATAR:
ÁREAS DE REGIONES TRIANGULARES
ÁREAS DE REGIONES DE LOS
CUADRILÁTEROS
ÁREAS DE REGIONES CIRCULARES
Lic. Pedro Luis Rojas Gómez

3. FÓRMULA BÁSICA:
• El área de la región de un triángulo
es igual al semiproducto de uno de
sus lados por su altura respectiva.
Lic. Pedro Luis Rojas Gómez

4. Ejemplos:
1. El área de la región de un triángulo es
27m2 y la longitud de su base es 3cm más
que su altura respectiva. Calcule dicha
altura.
2. Hallar el área de un triángulo rectángulo
cuyo perímetro es 240cm y sus lados
están en la relación 6, 8 y 10.
Lic. Pedro Luis Rojas Gómez

5. FÓRMULA DE HERÓN:
• El área de la región de un triángulo es igual a la raíz
cuadrada de su perímetro por los productos de las
diferencias del semiperímetro con cada uno de los
lados.
Lic. Pedro Luis Rojas Gómez

6. Ejemplos:
1. Una zona tiene forma triangular cuyos
lados miden 7cm, 9cm y 12cm. ¿Cuál es
el área de dicho triángulo?
2. Al medir los lados de un triángulo se tiene
como perímetro 120m. Si cada lado del
triángulo son entre si como 3, 4 y 5, ¿cuál
es su área?
Lic. Pedro Luis Rojas Gómez

7. FÓRMULA TRIGONOMÉTRICA:
• El área de la región de un triángulo es igual al
semiproducto de las longitudes de dos lados por la
razón trigonométrica seno de la medida del ángulo
que forman los dos lados tomados.
Algunos valores:
Sen 30º = ½ Sen45º = √2/2
Sen 60º = √3/2 Sen37º = 3/5
Sen 53º = 4/5 …
Lic. Pedro Luis Rojas Gómez

8. Ejemplos:
• Halla el área de los siguientes triángulos:
6cm 15cm
60º
7cm 30º
10cm
Lic. Pedro Luis Rojas Gómez

9. TRIÁNGULO EQUILÁTERO:
• El área de la región de un triángulo equilátero es
igual a la cuarta parte del cuadrado de la longitud de
su lado por la raíz cuadrada de tres.
Ejemplo:
• ¿Cuánto mide el
perímetro de un triángulo
equilátero de 15,57m2 de
área?
Lic. Pedro Luis Rojas Gómez

10. EN FUNCIÓN DEL INRADIO (r):
• El área de la región de un triángulo es igual al
producto de su semiperímetro y de la longitud de su
inradio (r).
Lic. Pedro Luis Rojas Gómez

11. EN FUNCIÓN DEL CIRCUNRADIO (R):
• El área de la región de un triángulo es igual al
producto de las longitudes de los tres lados, divididos
entre cuatro veces la longitud de su circunradio.
Lic. Pedro Luis Rojas Gómez

12. EN FUNCIÓN DEL EXRADIO (ra):
• El área de la región de un triángulo es igual a la
longitud de uno de sus exradios, multiplicado por la
diferencia del semiperímetro y de la longitud del lado
al cual es relativa la circunferencia exinscrita.
Lic. Pedro Luis Rojas Gómez

13. Práctica:
• En el rectángulo ABCD, encuentra el
área de la región sombreada, si
BF = 4cm y FC = 9cm.
• Encuentra el área de la región
sombreada del triángulo ABC, si
AC = 14cm y BH – DE = 6cm
• En un triángulo ABC, AB = 10cm,
m<A = 53º y m<C = 45º. Halla el
área de la región triangular.
Lic. Pedro Luis Rojas Gómez