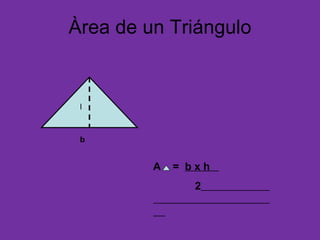
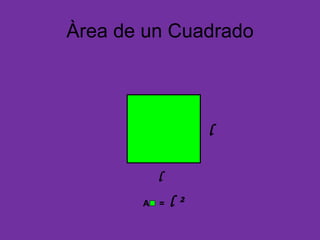
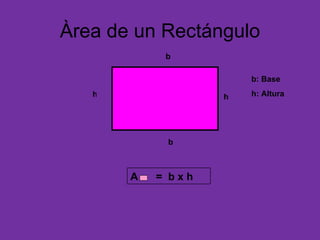
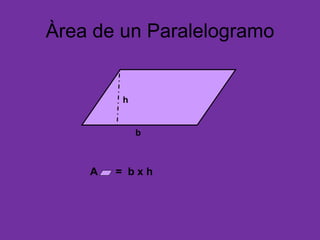
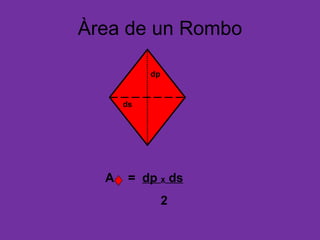
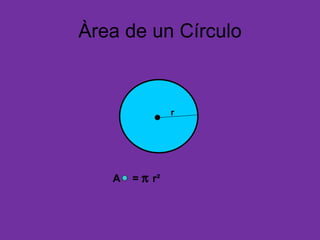
Este documento presenta las fórmulas para calcular el área de diferentes figuras geométricas como triángulos, cuadrados, rectángulos, trapecios, rombos, círculos y polígonos regulares. También incluye ejercicios de aplicación de estas fórmulas para hallar el área de figuras dadas sus medidas.

1. MATEMÀTICA Àreas de Regiones Poligonales

2. Àrea de un Triángulo h b A = b x h 2

3. Àrea de un Cuadrado l l A = l ²

4. Àrea de un Rectángulo b h h b b: Base h: Altura A = b x h

5. Àrea de un Paralelogramo h b A = b x h

7. Àrea de un Rombo dp ds A = dp x ds 2

8. Àrea de un Círculo r A =  r ²

9. Àrea de un Polígono Regular a a: Apotema El área de un polígono regular es igual a la mitad del producto de su perímetro por la apotema. A = P x a 2

10. Ejercicios 1.- Un terreno cuadrado tiene 516 metros de perímetro. ¿cuál es su área? P = 516 metros. Como es un cuadrado, dividimos entre 4 para hallar la medida de los lados. 516  4 = 129 metros. Cada lado mide 129 metros A = l ²  A = (129 m) ²  A = 16.641 m ²

11. 2.- La base de un rectángulo es de 24 cm y su altura es ¾ de su base. ¿Cuál es su área? a.- Determinamos la altura (h) ¾ x 24 = 72/4 = 18 cm b.- Aplicamos la fórmula: A = b x h = 24 cm x 18 cm = A = 432 cm ²

12. 3.- Si el perímetro de un cuadrado es de 24 cm, ¿cuál es el área de un círculo cuyo borde pasa por los vértices del cuadrado? a.- Determinar el lado del cuadrado: 24  4 = 6cm b.- Determinar el diámetro del círculo (Diagonal del cuadrado) para obtener el radio, aplicando teorema de Pitágoras. 6 cm 6 cm ? D ² = (6 cm)² + (6 cm)² D = √ 36 cm ² + 36 cm ² D= 8,48 cm  r= 8,48  2 = 4,24 cm c. Aplicamos la fórmula: A =  r ² A = 3,14 x (4,24 cm) ²  A = 3,14 x 17,97 cm ²  A = 56,42 cm ²

13. 4. Halle el área rayada en las siguientes figuras: 2 cm 2 cm 4 cm 2 cm 2 cm 6 cm 3 cm 4 cm 10 cm