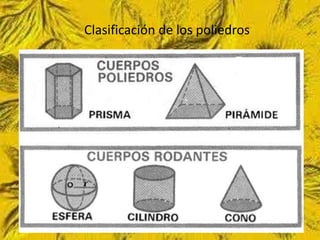
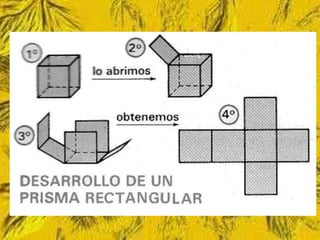
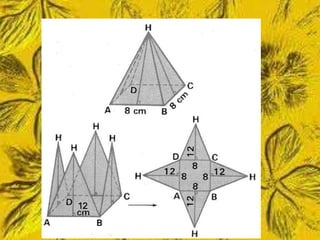
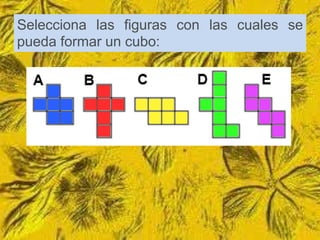
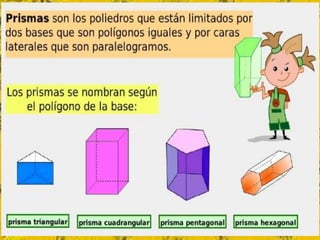
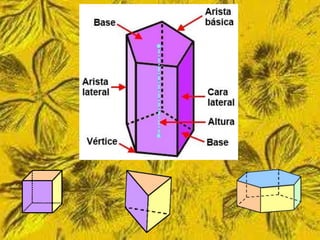
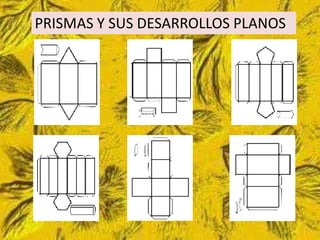
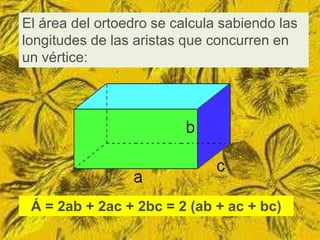
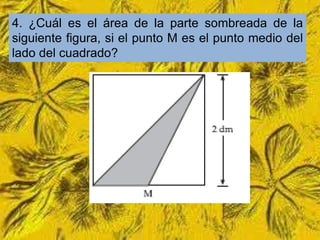
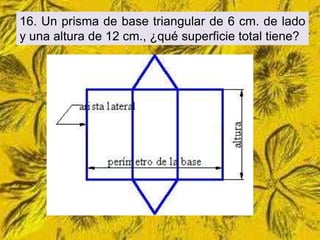
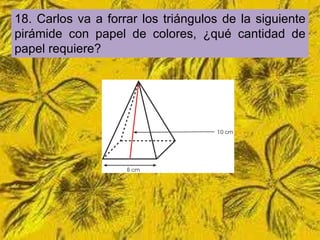
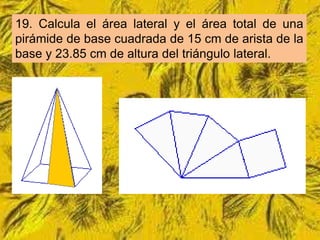
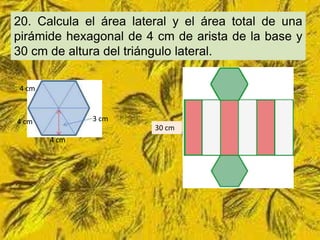
Este documento trata sobre cómo calcular el área lateral y el área total de prismas y pirámides. Explica que el área lateral de un prisma es la suma de las áreas de sus caras laterales, que forman un rectángulo cuya base es el perímetro de la figura de la base. El área total es la suma del área lateral más el doble del área de la base. También proporciona ejemplos numéricos de cómo calcular estas áreas para diferentes objetos tridimensionales.

1. Área lateral y
área total de
prismas y pirámides
http://www.ceibal.edu.uy/UserFiles/
P0001/ODEA/ORIGINAL/110908_pris
mas.elp/prisma_desarrollo.gif

3. Clasificación de los poliedros

6. Selecciona las figuras con las cuales se
pueda formar un cubo:

9. PRISMAS Y SUS DESARROLLOS PLANOS

10. El área lateral de un prisma es la suma de las áreas
de sus caras laterales.
Las caras laterales forman un rectángulo cuya base
es el perímetro de la figura geométrica de la base.
Por tanto, el área lateral del prisma es igual al
producto del perímetro de la base por la altura:
Área lateral = perímetro de la base x altura
El área total es la suma del área lateral más el área
de las 2 bases:
Área total = Área lateral + Área de la base x 2

11. Un cubo es un ortoedro cuyas tres aristas
tienen igual longitud. Su área es, por lo tanto:
Á = 6a²

12. El área del ortoedro se calcula sabiendo las
longitudes de las aristas que concurren en
un vértice:
Á = 2ab + 2ac + 2bc = 2 (ab + ac + bc)

13. Polígono regular
Un polígono regular es un polígono que tiene todos sus
lados y ángulos interiores iguales.
Características de un polígono regular
Lado es cada uno de los segmentos que forman el polígono.
Vértice es el punto en el que se encuentran dos lados.
Centro del polígono es el punto que equidista de todos los
vértices.
Apotema es el segmento que une el centro con un lado.
Radio es el segmento que une el centro con un vértice.
Perímetro es la suma de todos sus lados.

15. Área de polígonos regulares

17. 1,2. Se dispone de una tabla de madera de forma
cuadrada, como se muestra en la figura, a la cual se
le pretende dar una forma circular para que sirva de
tapa de un recipiente que tiene forma cilíndrica.
a)¿Qué área de la madera
se va a usar?
a)¿Cuál es el área de la
madera que no se va a
utilizar?
3.5 cm

18. Área del cuadrado
A = l x l
A = l2
A = 7cm x 7 cm.
A = 49 cm2
3.5 cm
As = A – Ac
As = 49 cm2 – 38.465 cm2
3.5 cm
As = 10.535 cm2.

19. a)¿Qué área de la madera se va a usar?
R = Se utiliza 38.465 cm2
a)¿Cuál es el área de la madera que no se va a
utilizar?
R = NO se utiliza 10.535 cm2
3.5 cm

20. 3. ¿Cuál es el área de la parte sombreada de la
siguiente figura, si el radio del círculo mide un
metro?

21. 4. ¿Cuál es el área de la parte sombreada de la
siguiente figura, si el punto M es el punto medio del
lado del cuadrado?

22. 5,6,7. La siguiente figura representa el vitral de una
ventana cuadrada que está formada por varios
cuadrados más pequeños. La parte del vitral que
tiene forma triangular es de color rojo y se quebró el
vidrio de la parte sombreada.
Al tratar de reparar el vitral:
¿Cuántos cm2 de vidrio rojo deberá utilizar quien la repare?
¿Cuántos cm2 de vidrio rojo usa este vitral?
¿Qué fracción del área total representa el triángulo rojo?

23. 8,9. La siguiente figura representa una ventana de
forma cuadrada que es parte de otro vitral:
M N
3dm = 30 cm
M es el punto medio del lado.
N es el punto medio entre M y el vértice.
¿Cuál es el área de cada uno de los triángulos
sombreados?
¿Qué representa el área de los triángulos
sombreados con respecto al cuadrado completo?1

24. 10,11,12. Calculemos el área total del siguiente prisma:
A) Calcular el área de las bases.
B) Calcular el área lateral.
C) Calcular su área total.

25. 13. Un industrial fabrica cajas cúbicas de 10 cm de
arista. ¿Qué cantidad mínima de cartón ocupa para
construir 100 cajas?
14,15. Las siguientes cajas tienen la misma
capacidad pero una de ellas requiere menos
cartón para ser construida. ¿Cuál de las dos
necesita menos cartón?
¿Qué cantidad de cartón se ahorraría el fabricante
al construir 100 cajas?

26. 16. Un prisma de base triangular de 6 cm. de lado
y una altura de 12 cm., ¿qué superficie total tiene?

27. 17. Calcula el área total de un prisma de base cuadrada
cuyo lado vale 2 cm. La altura del prisma es 5 cm.

28. 18. Carlos va a forrar los triángulos de la siguiente
pirámide con papel de colores, ¿qué cantidad de
papel requiere?

29. 19. Calcula el área lateral y el área total de una
pirámide de base cuadrada de 15 cm de arista de la
base y 23.85 cm de altura del triángulo lateral.

30. 20. Calcula el área lateral y el área total de una
pirámide hexagonal de 4 cm de arista de la base y
30 cm de altura del triángulo lateral.
4 cm
4 cm 3 cm
30 cm
4 cm