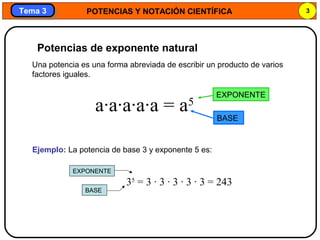
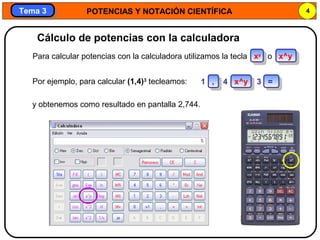
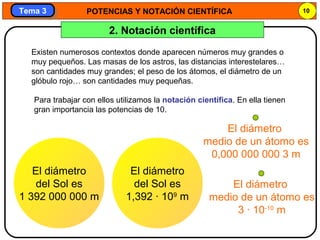
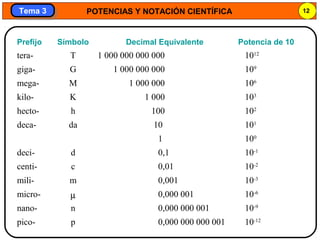
Este documento trata sobre potencias y notación científica. Explica las potencias de exponente negativo y cero, así como la notación científica y cómo expresar números grandes y pequeños usando potencias de 10. También cubre cómo realizar operaciones como suma, resta, multiplicación y división con números en notación científica.