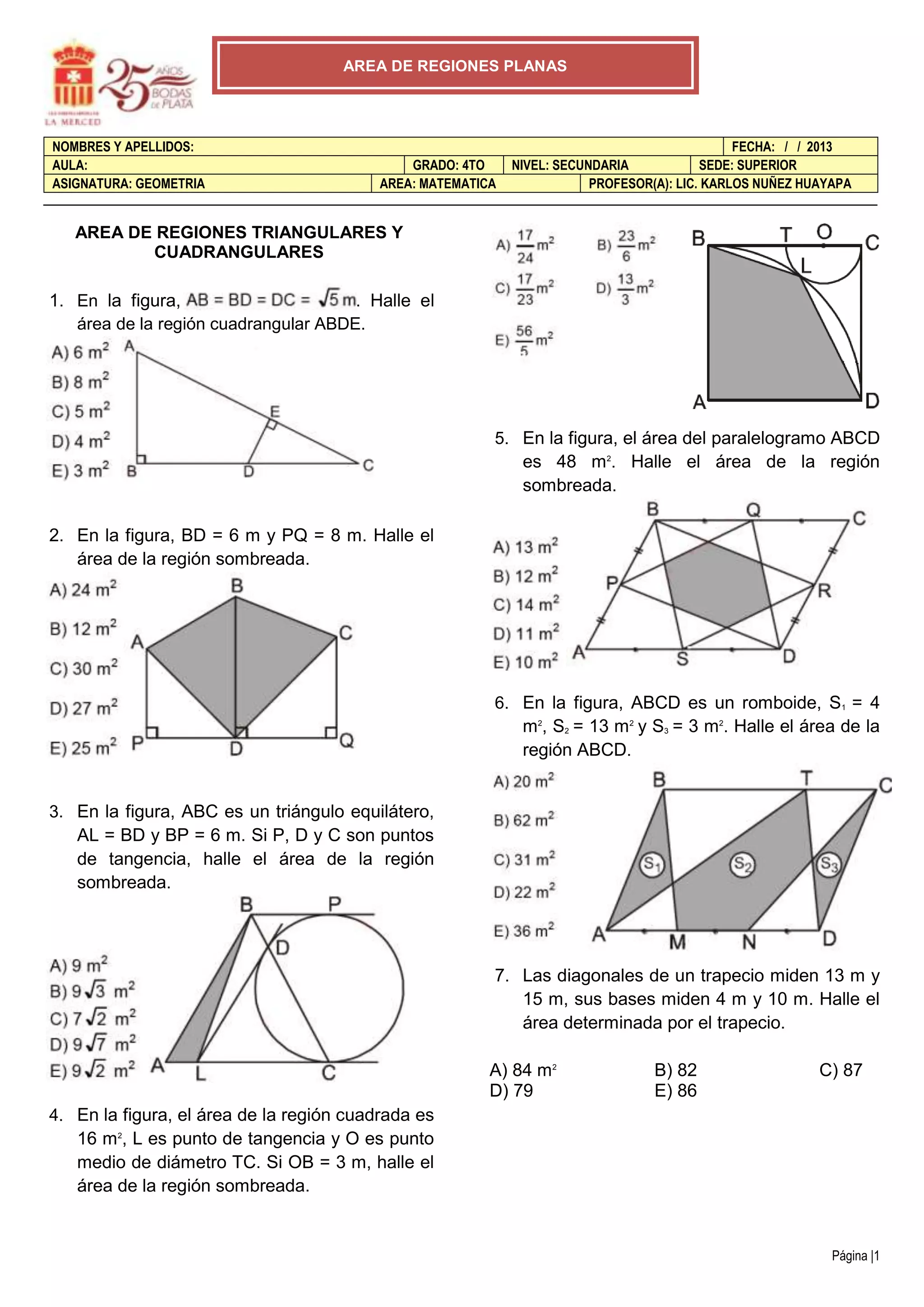
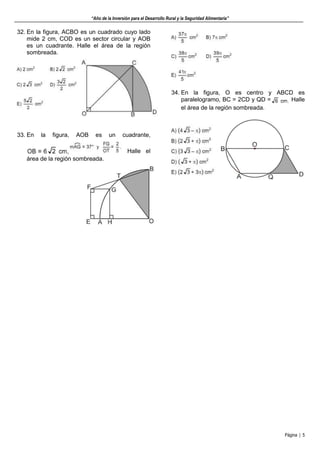
Este documento contiene 34 problemas de geometría sobre el cálculo de áreas de diferentes figuras planas como triángulos, cuadriláteros, trapecios, sectores y segmentos circulares. Los estudiantes deben resolver cada problema calculando el área de la región sombreada dadas las medidas de los lados u otros datos como puntos medios o de tangencia. El documento proporciona las figuras y datos necesarios para cada problema pero no incluye las soluciones.

1. Página |1
NOMBRES Y APELLIDOS: FECHA: / / 2013
AULA: GRADO: 4TO NIVEL: SECUNDARIA SEDE: SUPERIOR
ASIGNATURA: GEOMETRIA AREA: MATEMATICA PROFESOR(A): LIC. KARLOS NUÑEZ HUAYAPA
AREA DE REGIONES PLANAS
AREA DE REGIONES TRIANGULARES Y
CUADRANGULARES
1. En la figura, . Halle el
área de la región cuadrangular ABDE.
2. En la figura, BD = 6 m y PQ = 8 m. Halle el
área de la región sombreada.
3. En la figura, ABC es un triángulo equilátero,
AL = BD y BP = 6 m. Si P, D y C son puntos
de tangencia, halle el área de la región
sombreada.
4. En la figura, el área de la región cuadrada es
16 m2
, L es punto de tangencia y O es punto
medio de diámetro TC. Si OB = 3 m, halle el
área de la región sombreada.
5. En la figura, el área del paralelogramo ABCD
es 48 m2
. Halle el área de la región
sombreada.
6. En la figura, ABCD es un romboide, S1 = 4
m2
, S2 = 13 m2
y S3 = 3 m2
. Halle el área de la
región ABCD.
7. Las diagonales de un trapecio miden 13 m y
15 m, sus bases miden 4 m y 10 m. Halle el
área determinada por el trapecio.
A) 84 m2
B) 82 C) 87
D) 79 E) 86

2. “Año de la Inversión para el Desarrollo Rural y la Seguridad Alimentaria”
Página | 2
8. En la figura, AD = 8 m, BC = 2 m y EB = BD.
Halle el área de la región ABCD.
9. En la figura, BM = 2 m y MN = 3 m. Si N es
punto de tangencia, halle el área de la región
sombreada.
10. En la figura, O es centro de la circunferencia
cuyo radio mide 2 m, AB = BC y EM = MF.
Halle el área de la región sombreada.
11. En la figura, . Halle el área de la
región rectangular ABCD.
12. En la figura, G es baricentro del triángulo
ABC, AE = 8 m y BE = 18 m. Si el área de la
región sombreada es 15 m2
. Halle el área de
la región triangular ABC.
13. En la figura, AM = MD. Si el área de la
región sombreada POM es 3 m2
, halle el
área de la región rectangular ABCD.
14. En la figura, el área de la región determinada
por el paralelogramo ABCD es 120 m2
y M es
punto medio de AD. Halle el área de la
región sombreada
15. En la figura, AMNQ es un paralelogramo. Si
las áreas de las regiones triangulares MBN y
QNC son 4 m2 y 9 m2, respectivamente,
halle el área de la región triangular AMQ.

3. “Año de la Inversión para el Desarrollo Rural y la Seguridad Alimentaria”
Página | 3
16. En la figura, I es incentro del triángulo ABC.
Si AB = 9 m y BC = 12 m, halle el área de la
región sombreada.
17. En un rombo, las proyecciones de las
diagonales sobre uno de sus lados miden 12
m y 3 m. Halle el área de la región limitada
por dicho rombo.
A) 36 m2
B) 18 C) 42 D) 45 E) 64
18. En la figura, el área de la región rectangular
ABCD es 60 m2
. Si M y N son puntos
medios, halle la suma de las áreas de las
regiones sombreadas.
19. En la figura, AM = MB, CN = NB,
. Si el área de las
regiones triangulares MPQ y QRN son 4 m2
y 9 m2, halle el área de la región triangular
ABC.
20. En la figura, AB = BD, 5AD = 6DC y AC =
1m. Hallar el área de la región triangular
BDC
21. En la figura, CM = MD. Si el área de la region
sombreada es 10m2
, hallar el área de la region
rectangular ABCD
AREA DE REGIONES CIRCULARES
22. En la figura, AOB es un sector circular. Si
, OA = 3 m y M, N y P son
puntos de tangencia, hallar el área de la región
sombreada.
23. En la figura, AC es diámetro, PM = 2 m y QN
= 4 m. Si M y N son puntos medios de AB y
BC, hallar el área del círculo sombreado
inscrito.

4. “Año de la Inversión para el Desarrollo Rural y la Seguridad Alimentaria”
Página | 4
24. En la figura, O es punto de tangencia, O y O1
son puntos medios de los diámetros AB y MN.
Si MN = 12 cm, hallar el área de la región
sombreada.
25. En la figura, O es punto medio del diámetro
AC. Si las áreas de las regiones sombreadas
son S1 = 7 m2
y S2 = 41 m2
, hallar el área del
sector circular DOC.
26. En la figura, AOB es un cuadrante, AO es
diámetro, AQ = QO y OB = Hallar el
área de la región sombreada.
27. En la figura, AM = 4 m, NC = 16 m, O es punto
medio del diámetro DE, M y N son puntos de
tangencia. Hallar el área de la región
sombreada.
28. En la figura, O es punto medio del diámetro
EF y ABCD es un cuadrado cuyo lado mide 2
m. Hallar el área de la región sombreada.
29. En la figura, AB = 6 cm, A es centro del arco
, O es punto medio del diámetro AC y
ABC es un triángulo equilátero. Hallar el área
de la región sombreada.
30. En la figura, AOB es un cuadrante, O1 es
punto medio del diámetro AO y O2 es centro.
Si el área del círculo de centro O2 es 63π m2
,
hallar el área de la región sombreada.
31. En la figura, O es centro de la
semicircunferencia y AB = 8 cm. Si S3 = S1 +
S2, hallar la longitud del radio de la
circunferencia.

5. “Año de la Inversión para el Desarrollo Rural y la Seguridad Alimentaria”
Página | 5
32. En la figura, ACBO es un cuadrado cuyo lado
mide 2 cm, COD es un sector circular y AOB
es un cuadrante. Halle el área de la región
sombreada.
33. En la figura, AOB es un cuadrante,
Halle el
área de la región sombreada.
34. En la figura, O es centro y ABCD es
paralelogramo, BC = 2CD y QD = Halle
el área de la región sombreada.