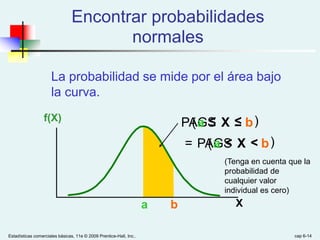
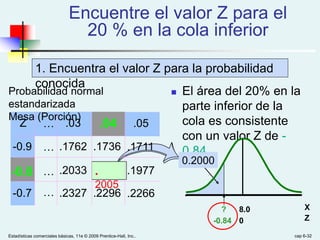
Este documento presenta el Capítulo 6 de un libro de texto sobre estadísticas comerciales básicas. El capítulo cubre distribuciones de probabilidad continuas como la distribución normal, uniforme y exponencial. Explica cómo calcular probabilidades a partir de estas distribuciones y la conversión a la distribución normal estandarizada. También presenta reglas empíricas sobre la dispersión de valores alrededor de la media para la distribución normal.