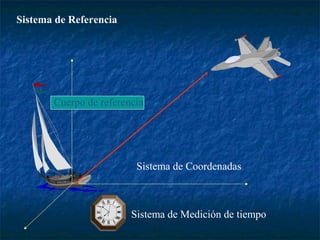
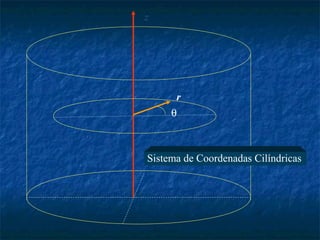
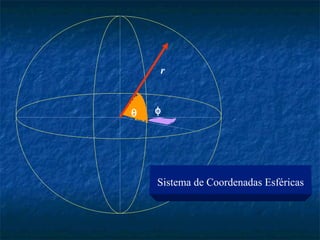
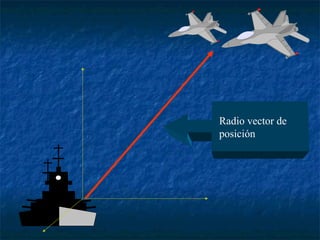
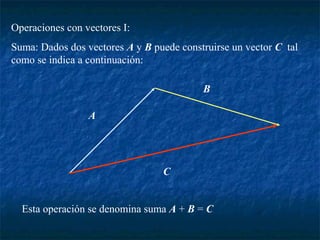
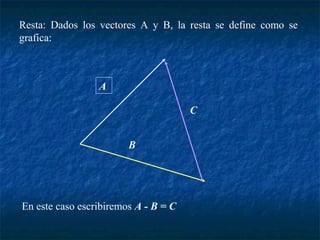
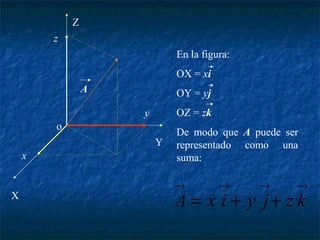
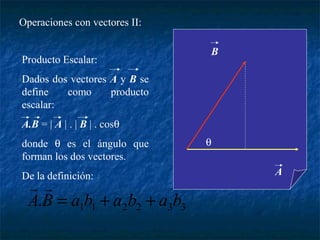
Este documento presenta los conceptos básicos de vectores y cálculo vectorial, incluyendo definiciones de vectores, operaciones con vectores, sistemas de coordenadas, derivación e integración vectorial, y operadores vectoriales como gradiente, divergencia y rotacional.

1. BBaasseess FFííssiiccaass ddee
llaa FFiissiioollooggííaa

2. AAllggeebbrraa
yy
CCáállccuulloo VVeeccttoorriiaall

3. Sistema de Referencia
Cuerpo de referencia
Sistema de Coordenadas
Sistema de Medición de tiempo

4. z
r
q
Sistema de Coordenadas Cilíndricas

5. r
q f
Sistema de Coordenadas Esféricas

6. Radio vector de
posición

7. Definiciones:
Vector: Objeto matemático para cuya completa definición se
requiere indicar su magnitud (representada por un número
natural) así como su dirección y sentido.
Se conviene que la longitud del vector es proporcional o igual a
la magnitud del vector. Los vectores se representan mediante
segmentos de recta dirigidos.
A
La magnitud del vector se escribe | A | = A

8. Operaciones con vectores I:
Suma: Dados dos vectores A y B puede construirse un vector C tal
como se indica a continuación:
A
B
C
Esta operación se denomina suma A + B = C

9. Resta: Dados los vectores A y B, la resta se define como se
grafica:
A
B
C
En este caso escribiremos A - B = C

10. Multiplicación por un escalar:
Podemos multiplicar un vector por un escalar. El resultado es
un vector que mantiene la dirección y sentido pero cuya
magnitud es la anterior multiplicada por la constante escalar.
A
3A

11. Componentes de un vector:
Proyeción de un vector sobre
cada uno de los ejes
cartesianos.
Definimos sobre cada eje un
vector cuya longitud es 1
(vector unitario). Cada
proyección puede ser
representada en función del
vector unitario respectivo.
Los vectores unitarios son:
eje OX : i
eje OY : j
eje OZ : k

12. A
x
y
z
o
X
Y
Z
En la figura:
OX = xi
OY = yj
OZ = zk
De modo que A puede ser
representado como una
suma:
® ® ® ®
A = x i + y j+ z k

13. Con esta nueva notación la suma podrá reescribirse para dos
vectores:
  
A = a i + a j +
a k
1 2 3
= + +
  
B b i b j b k
1 2 3
  
A B a b i a b j a b k
( ) ( ) ( ) 1 1 2 2 3 3 + = + + + + +
y la resta:
A B a b i a b j a b k
  
( ) ( ) ( ) 1 1 2 2 3 3 - = - + - + -

14. Operaciones con vectores II:
B
Producto Escalar:
Dados dos vectores A y B se
define como producto
escalar:
A.B = | A | . | B | . cosq
donde q es el ángulo que
q
forman los dos vectores.
De la definición: A
 
1 1 2 2 3 3 A.B = a b + a b + a b

15. Producto vectorial:
Se define como producto
vectorial de los vectores A y
B al vector V tal que
V = A ´ B = [A B]
es perpendicular a A y B a
la vez y cuya magnitud se
define como:
| V | = | A |.| B | senq
Puede verse que la
magnitud del vector V es
igual al área definida por A
y B.
Observe el sentido de la
rotación.
B
A
V
q

16. Propiedades:
A + B = B + A
A - B = - (B - A)
c(A + B) = cA + cB
A.B = B.A
A.(B + C) = A.B + A.C
A.(B + C) = (B + C).A
A.A = | A |2
[A B] = - [B A]
[A (B + C)] = [A B] + [A C]
A.[C B] = B.[A C] = C.[B A]
[A [B C]] = (A.C)B - (A.B)C
TTaarreeaa:: DDeemmoossttrraarr llaass
aanntteerriioorreess rreellaacciioonneess

17. El producto vectorial puede obtenerse mediante el determinante:
  
i j k
a a a
´ = =
1 2 3
b b b
 
A B
1 2 3
  
a b a b i a b a b j a b a b k
= - - - + -
( ) ( ) ( ) 2 3 3 2 1 3 3 1 1 2 2 1

18. Existe el llamado triple escalar :
[ ]
ABC A .
B C
A A A
1 2 3
B B B
1 2 3
C C C
1 2 3
=
= ´ =

19. DDeerriivvaacciióónn::
Una magnitud vectorial es derivable respecto a un
parámetro escalar, por ejemplo, el tiempo:
d      = + + =
j dz
dt
k v
dt
r dx
dt
i dy
dt
Hemos obtenido una nueva magnitud vectorial denominada
VELOCIDAD.

20. También podemos calcular la
variación de una magnitud
escalar respecto a la dirección.
Por ejemplo, podemos calcluar la
variación de densidad del aire
respecto a la altura (eje Z).
O también podemos calcular la
variación de la temperatura del
agua respecto a la profundidad
(eje Z).
O podemos calcular la variación
de la población de determinada
especie a medida que nos
alejamos de una fuente de
alimento (radio R)

21. Sea P la magnitud escalar, entonces la variación direccional de
P se expresará como:
dP   
j dP
k
dz
i dP
dx
+ +
dy
Es, evidentemente, una magnitud vectorial. Se denomina
GRADIENTE de P. “Factorizando” el operador de derivación
direccional, escribiremos finalmemente:
æ
= + +
grad P d ÷ ÷ø
j d
k P
dz
i d
dx
dy
ö
ç çè
  

22. Por otro lado, si deseamos conocer como varía la magnitud
de un vector A con la dirección, escribiremos:

+ +
dA 
j dA
k
dz
i dA
dx
dy




Si recordamos que:
   
= + +
A a i a j a k x y z
vemos que cada término es un producto escalar, y que la
operación da como resultado un escalar.

23. Esta operación se denomina DIVERGENCIA del vector A, y
se escribe:
    
æ
= + +
j d
ö
k A
dz
i d
dx
dy
div A d
. ÷ ÷ø
ç çè
Puede apreciarse que se ha realizado una operación de
producto escalar entre el operador de variación direccional y la
magnitud vectorial analizada.

24. Finalmente, si el vectort A gira, incluye el giro en su
desplazamiento en en el espacio, la operación que nos permite
conocer la variación de las componentes de A al girar se
denomina rotor o rotacional de A, y se escribe:
    
æ
= + +
j d
ö
k A
dz
i d
dx
dy
rot A d
´ ÷ ÷ø
ç çè
Es una operación de producto vectorial, y para calcularla se
aplica el determinante previemente visto en la primera parte de
este curso.

25. Resumiendo, si denotamos mediante Ñ (nabla) el operador de
variación direccional, las tres operaciones de derivación
direccional pueden reescribirse:
  
j d
ö
æ
     
j d
j d
ö
ö
k A
dz
i d
dx
i d
dx
i d
dx
dy
æ
æ
A rot A d
k A
dz
dy
A div A d
k P
dz
dy
P grad P d
     
´ ÷ ÷ø
ç çè
Ñ´ = = + +
· ÷ ÷ø
ç çè
Ñ = = + +
÷ ÷ø
ç çè
Ñ = = + +
.