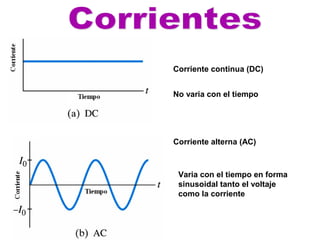
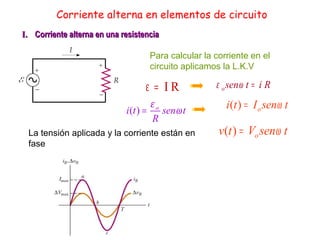
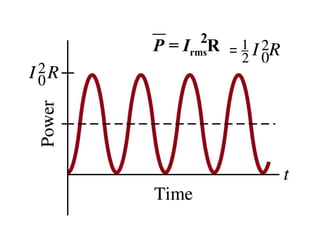
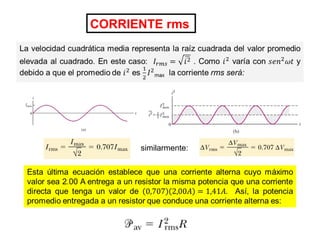
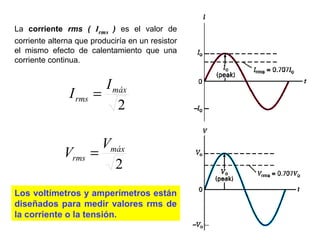
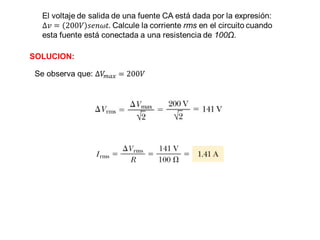
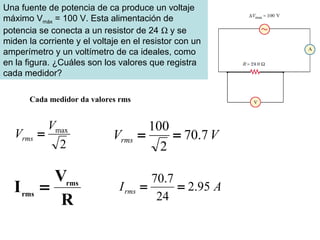
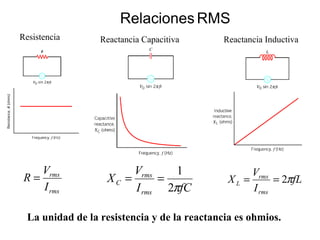
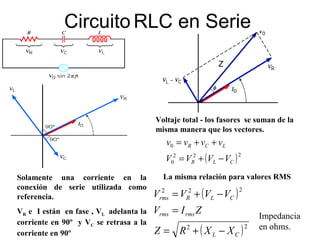
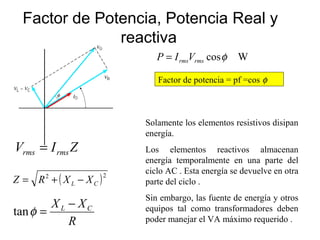
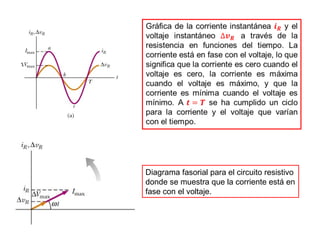
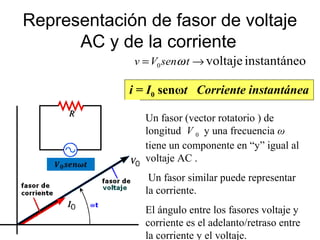
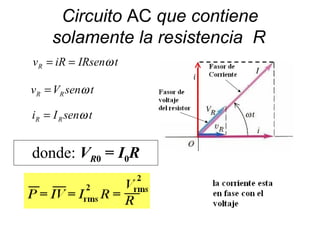
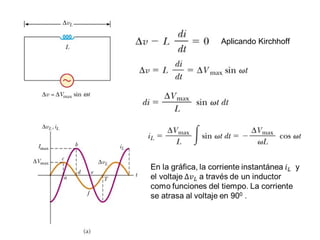
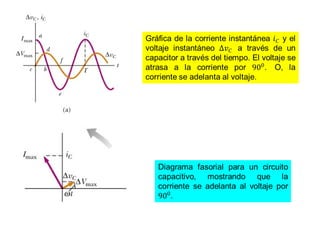
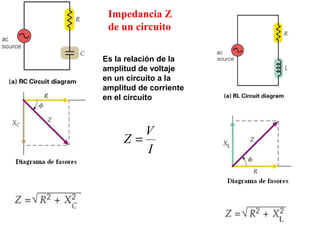
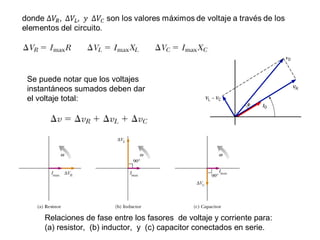
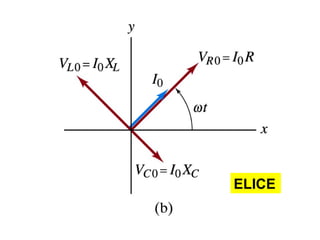
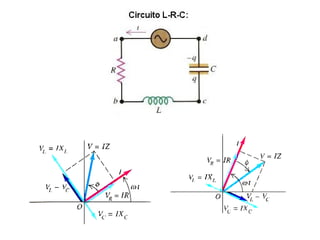
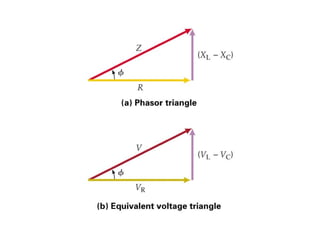
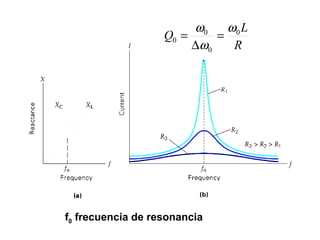
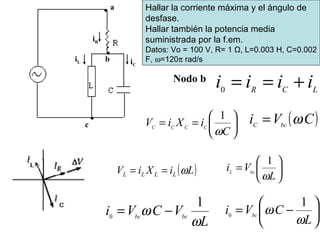
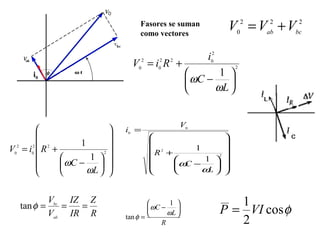
Este documento resume conceptos clave sobre corriente continua (DC) y corriente alterna (AC), incluyendo: - La corriente DC no varía con el tiempo mientras que la corriente AC varía de forma sinusoidal. - Los voltímetros y amperímetros miden valores eficaces (rms) de voltaje y corriente para circuitos AC. - Los diagramas fasoriales representan voltajes y corrientes AC como vectores giratorios que permiten analizar las diferencias de fase.

2. Corriente continua (DC)
Corriente alterna (AC)
No varia con el tiempo
Varia con el tiempo en forma
sinusoidal tanto el voltaje
como la corriente

3. Un circuito que consiste de una resistencia
R conectada a una fuente CA, designada
por el símbolo
0=∆+∆ Rvv Reglas de Kirchhoff.
tsenItsen
R
V
R
v
i R
R max
max
ωω =
∆
=
∆
=

4. Diagrama fasorial para el circuito resistivo
donde se muestra que la corriente está en
fase con el voltaje.

5. CORRIENTE rms
similarmente:

6. La corriente rms ( Irms ) es el valor de
corriente alterna que produciría en un resistor
el mismo efecto de calentamiento que una
corriente continua.
2
máx
rms
I
I =
2
máx
rms
V
V =
Los voltímetros y amperímetros están
diseñados para medir valores rms de
la corriente o la tensión.

7. SOLUCION:

8. Valor Eficaz (Rms)
• Éstos significan la misma cosa para los
circuitos AC :
– “voltaje de C.C. equivalente ”
– “voltaje eficaz ”
– “voltaje rms”
– RMS = root mean square
max
2
1
VVVV rmseffequivalentDC ===

9. Corriente alterna en elementos de circuito
I.I. Corriente alterna en una resistenciaCorriente alterna en una resistencia
La tensión aplicada y la corriente están en
fase
tsen
R
ti o
ω
ε
=)(
tsenIti o ω=)(
Para calcular la corriente en el
circuito aplicamos la L.K.V
RI=ε Ritseno =ωε
tsenVtv o ω=)(

10. Notación fasorial
La corriente y el voltaje pueden representarse mediante vectores
bidimensionales llamados fasores.
El valor instantáneo de la caída de tensión es la
componente y del vector VR, que gira en sentido
antihorario con una velocidad ω.
A sen(ωt-δ1) Fasor A ( )A

B sen(ωt-δ2) Fasor B ( )B
 BAC

+=
Uso de los fasores
Combinar cantidades
sinusoidales con diferencias
de fase utilizando fasores se
convierte en una suma de
vectores.

11. Representación de fasor de voltaje
AC y de la corriente
oinstantánevoltaje0 →= tsenVv ω
Un fasor (vector rotatorio ) de
longitud V 0 y una frecuencia ω
tiene un componente en “y” igual al
voltaje AC .
Un fasor similar puede representar
la corriente.
El ángulo entre los fasores voltaje y
corriente es el adelanto/retraso entre
la corriente y el voltaje.
i = I0 senωt Corriente instantánea

12. Relación De Fase
θ = ángulo de fase
• Para adelanto θ°
v=Vpcos(ωt+θ)
• Para retraso θ°
v=Vpcos(ωt-θ)

13. Circuito AC que contiene
solamente la resistencia R
donde: VR0 = I0R
tIRseniRvR ω==
tsenVv RR ω=
tsenIi RR ω=

14. P = IrmsR2

15. Cada medidor da valores rms
2
maxV
Vrms = VVrms 7.70
2
100
==
R
V
I rms
rms
= AIrms 95.2
24
7.70
==
Una fuente de potencia de ca produce un voltaje
máximo Vmáx = 100 V. Esta alimentación de
potencia se conecta a un resistor de 24 Ω y se
miden la corriente y el voltaje en el resistor con un
amperímetro y un voltímetro de ca ideales, como
en la figura. ¿Cuáles son los valores que registra
cada medidor?

16. Ω6.184.102.8 =+=TotalR A
R
V
I
Total
circuito 806.0
6.18
15
===
RIP altavozaltavoz
2
2
1
= ( ) WPaltavoz 38.34.10806.0
2
1 2
=×=
Un amplificador de audio, representado por
medio de la fuente de ca y de un resistor en la
figura, entrega a un altavoz voltaje alterno a
frecuencias de audio. Si el voltaje de salida tiene
una amplitud de 15.0 V, R= 8.20 Ω, y el altavoz
es equivalente a una resistencia de 10.4 Ω, ¿cuál
es la potencia promedio en el tiempo que se le
entrega?

17. Las tres lámparas están en
paralelo
V
P
II 1
21 == AII 25.1
120
150
21 ===
2
1
1 96
25.1
120
R
I
V
R ==== Ω
A
V
P
I 833.0
120
1003
3 === Ω144
833.0
120
3
3 ===
I
V
R
AIIIItotal 33.3833.025.125.1321 =++=++=
La figura muestra tres lámparas conectadas a un
suministro de voltaje doméstico de 120 V ca
(rms). Las lámparas 1 y 2 tienen focos de 150 W y
la lámpara 3 tiene un foco de 100 W. Encuentre la
corriente rms y la resistencia de cada foco.

18. Aplicando Kirchhoff

19. Diagrama fasorial para un circuito
inductivo, mostrando que la corriente
se atrasa al voltaje en 900
.

20. Note que el voltaje alcanza su valor máximo un cuarto de periodo antes que
la corriente alcance su valor máximo. Por lo tanto decimos que:
L
V
I
ω
max
max
∆
=
Esta expresión se parece al de la corriente máxima en un sistema resistivo.
R
V
I max
max
∆
=

21. REACTANCIA
INDUCTIVA
Considere un circuito AC como en la figura. La frecuencia de la fuente CA se
regula mientras su amplitud de voltaje se mantiene constante. El foco brillará a
su máximo si: (a) altas frecuencias (b) bajas frecuencias (c) el brillo será el
mismo a todas las frecuencias.
Para bajas frecuencias, la reactancia
inductiva será pequeña, de modo que la
corriente será máxima y el foco brillará
más.

22. En un circuito CA puramente inductivo, L = 25,0 mH y el voltaje rms es 150 V.
Calcule la reactancia inductiva y la corriente rms en el circuito si la frecuencia
es 60.0 Hz.
Ω= 42.9LX
¿Qué pasaría con la corriente rms en el circuito si la frecuencia se incrementara
a 6.00 KHz?

23. CAPACITORES EN CIRCUITOS CA
Aplicando Kirchhoff
tsenVCvCq C ωmax∆=∆=
Usando la identidad trigonométrica:

25. maxmax VCI ∆= ω
C
V
I
ω
1
max
max
∆
=
Como en el caso de los inductores, el denominador hace el rol de la
resistencia cuyas unidades son ohms y recibe el nombre de reactancia
capacitiva.
tsenVvC ωmax∆=∆
tsenXIv CC ωmax=∆

26. Considere el circuito CA de la figura. La frecuencia de la fuente CA se ajusta
mientras su amplitud de voltaje se mantiene constante. El foco brillará mas
para: (a) altas frecuencias (b) bajas frecuencias (c) el brillo será el mismo
para todas las frecuencias.
El foco brillará más para altas
frecuencias.

27. Considere el circuito CA de la figura. La frecuencia de la fuente CA es ajustada
mientras su amplitud de voltaje se mantiene constante. El foco brillará más
para: (a) altas frecuencias (b) bajas frecuencias (c) el brillo será el mismo
para todas las frecuencias.
El foco brillará más para bajas frecuencias.

28. 1
3772 −
== sfπω
Si la frecuencia se duplicara, ¿cuál sería el valor de la corriente rms? Si la
frecuencia se incrementa, la reactancia capacitiva decrece (lo opuesto a lo
que ocurre con el inductor). El decrecimiento de la reactancia capacitiva
resulta en un incremento en la corriente.
La nueva reactancia capacitiva sería:

29. Ejemplo Reactancia de una bobina.
(a) se aplican 120-V dc;
(b) se aplican 120-V ac (rms) a 60.0 Hz.
A
R
V
I 120
1
120
===
LIV L
ω=
Lf
V
L
V
I rmsL
πω 2
2
==
( )
AI 5.1
3.0602
1202
==
π

30. Ω3.13
5.7
100
===
I
V
XL
( )
H
f
XX
L LL
0424.0
502
3.13
2
====
ππω
Ω40
5.2
100
===
I
V
XL
s
rad
L
XL
943
0424.0
40
===ω
a)
b)
En un circuito de ca puramente inductivo, como
en la figura, Vmax = 100 V. a) Si la corriente
máxima es 7.5 A a 50 Hz, calcule la inductancia L.
b) ¿A qué frecuencia angular ω la corriente
máxima es 2.5 A?
XL = ωL

31. Ejemplo Reactancia del condensador.
Cuáles son la corriente pico y rms en el circuito
mostrado si C = 1.0 µ F y Vrms = 120 V? Calcular
para f = 60 Hz
C
I
VC
ω
=
( )CfVI C
π2= ( )CfVI rms
π22=
( )( ) A.IMax
06401016021202 6
=×= −
π
A.
.
.I
I Max
rms
0450
411
0640
2
===
( )Cf
I
VC
π2
=

32. ( ) VVV rms 3.282022max ===
maxmax CVQ
C
Q
VC =→=
( ) nCQ 77.23.281098 12
max =×= −
Un capacitor de 98.0 pF está conectado a un suministro de
potencia de 60.0 Hz que produce un voltaje rms de 20.0 V.
¿Cuál es la carga máxima que aparece en cualesquiera de las
placas del capacitor?

33. a) ¿Para qué frecuencias lineales un capacitor de 22.0 μF
tiene una reactancia por debajo de 175 Ω? b) Sobre este
mismo intervalo de frecuencia, ¿cuál es la reactancia de un
capacitor de 44.0 μF?

34. Relaciones RMS
Resistencia
rms
rms
I
V
R =
Reactancia Capacitiva
fCI
V
X
rms
rms
C
π2
1
==
Reactancia Inductiva
fL
I
V
X
rms
rms
L π2==
La unidad de la resistencia y de la reactancia es ohmios.

35. Potencia
Resistencia Capacitancia Inductancia
RIP rms
2
=
La energía disipada
en un resistor se
convierte en calor.
Crms XIP 2
= Lrms XIP 2
=
El condensador es un
dispositivo de almacenaje
de la energía.
Durante el ciclo la
energía se almacena
temporalmente en el
campo eléctrico.
Por lo tanto, la potencia
no es una potencia
verdadera sino potencia
reactiva llamada en
unidades de voltio-
amperio-reactivo (VAR).
El inductor es un dispositivo
de almacenaje de la energía.
Durante el ciclo AC la
energía se almacena
temporalmente en el campo
magnético
La potencia no es potencia
verdadero sino reactiva en
unidades VAR.

36. Impedancia Z
de un circuito
Es la relación de la
amplitud de voltaje
en un circuito a la
amplitud de corriente
en el circuito
I
V
Z =

37. CIRCUITOS RLC EN SERIE
La figura muestra un circuito que contiene un resistor, un inductor, y un
capacitor conectados en serie a través de una fuente de voltaje alternante.
Como antes, asumimos que el voltaje aplicado varía sinusoidalmente con el
tiempo. Es conveniente suponer que el voltaje aplicado instantáneo está dado
por:

38. Se puede notar que los voltajes
instantáneos sumados deben dar
el voltaje total:
Relaciones de fase entre los fasores de voltaje y corriente para:
(a) resistor, (b) inductor, y (c) capacitor conectados en serie.

39. Del gráfico (b):
Por lo tanto la máxima corriente es:
El denominador de la ecuación anterior se denomina IMPEDANCIA Z

40. SUS UNIDADES SON OHMIOS
El triángulo de
impedancia para un
circuito RLC en serie
da la relación:

42. R
XX CL −
=φtan
φtanRXX CL +=
( ) ( )( ) ( )





−Ω+
×
= −−−
0
611
60tan200
1000.40.602
1
0.602
1
ss
L
ππ
HL 84.0=

43. b) Calcule la máxima corriente en el circuito.
c) Encuentre el ángulo de fase entre la corriente y el voltaje
0
34−=φ

44. d) Calcule el máximo voltaje y el voltaje instantáneo a través de cada
elemento.
Los máximos voltajes son:
Los voltajes instantáneos son:

45. Cf
XC
π2
1
= ( )( ) Ω8
12
1033.1
1020602
1
×=
×
= −
πCX
22
CXRZ += ( ) ( ) Ω82823
1033.11033.11050 ×=×+×=Z
A
Z
V
I 5
8
1077.3
1033.1
5000 −
×=
×
== personapersona IRV =
( ) VVpersona 88.110501077.3 35
=×××= −
Una persona está trabajando cerca del secundario de
un transformador, como se muestra en la figura. El
voltaje primario es 120 V a 60 Hz. La capacitancia Ci,
que es la capacitancia entre la mano y el devanado
secundario, es 20.0 pF. Suponiendo que la persona
tiene una resistencia de cuerpo a tierra Re = 50.0 k Ω.
determine el voltaje rms a través del cuerpo.
Sugerencia: Redibuje el circuito con el secundario del
tranformador como una fuente de ca simple.

46. Circuito RLC en Serie
Solamente una corriente en la
conexión de serie utilizada como
referencia.
VR e I están en fase , VL adelanta la
corriente en 90º y VC se retrasa a la
corriente en 90º
Voltaje total - los fasores se suman de la
misma manera que los vectores.
( )222
0
0
CLR
LCR
VVVV
vvvv
−+=
++=
La misma relación para valores RMS
( )
( )22
222
CL
rmsrms
CLRrms
XXRZ
ZIV
VVVV
−+=
=
−+=
Impedancia
en ohms.
Z

47. ELICE

50. POTENCIA EN UN CIRCUITO CA
La potencia instantánea entregada por una fuente CA a un circuito es el
producto de corriente de la fuente y el voltaje aplicado.
Para un circuito RLC en serie, se puede expresar la potencia instantánea
como:
Promedio = 0
Expresando esta potencia en términos
de la corriente y voltaje rms, queda:

51. Remplazando en la ecuación anterior
Válido para carga
resistiva solamente.
No existen pérdida de potencia en circuitos CA puramente
capacitivos o puramente inductivos.

52. a)
b)
c)

53. Factor de Potencia, Potencia Real y
reactiva
ZIV rmsrms =
Factor de potencia = pf =cos φ
WcosφrmsrmsVIP =
Solamente los elementos resistivos disipan
energía.
Los elementos reactivos almacenan
energía temporalmente en una parte del
ciclo AC . Esta energía se devuelve en otra
parte del ciclo .
Sin embargo, las fuente de energía y otros
equipos tal como transformadores deben
poder manejar el VA máximo requerido .
( )22
CL XXRZ −+=
R
XX CL −
=φtan

54. R
L
Q 0
0
0
0
ω
ω
ω
=
∆
=
f0 frecuencia de resonancia

55. La fuente de voltaje en la figura tiene una
salida V = (100 V) cos( 1000t ). Determine a) la
corriente en el circuito y b) la potencia
suministrada por la fuente, c) Muestre que la
potencia disipada en el resistor es igual a la
potencia suministrada por la fuente.
XL = ωL XL = 1000(50x10-3
)=50Ω
1
C
XC
ω
=
( ) Ω=
×
= −
20
10501000
1
6CX
( )22
CL XXRZ −+=
( ) Ω=−+= 50205040
22
Z

56. La fuente de voltaje en la figura tiene una
salida V = (100 V) cos( 1000t ). Determine a) la
corriente en el circuito y b) la potencia
suministrada por la fuente, c) Muestre que la
potencia disipada en el resistor es igual a la
potencia suministrada por la fuente.
ZIV rmsrms =
R
XX CL −
=φtan
A
Z
V
I 2
50
100max
max ===
o
9.36
40
2050
tan 1
=




 −
= −
φ
cosIVP φ
2
1
= W.cosP 809361002
2
1
=×=
RIP 2
0
2
1
= ( ) WP 80402
2
1 2
==

57. Ω=×= 5005.01000LX
Ω=
××
= −
200
100.51000
1
6CX
( )22
CL XXRZ −+= ( ) ( ) Ω500200500400
22
=−+=Z
Z
V
I max
max =
AI 2.0
500
100
max ==
RIP 2
max
2
1
= ( ) WP 0.84002.0
2
1 2
==
Un voltaje de ca de la forma v = (100 V) sen(1000t) se aplica a un
circuito RLC en serie. Si R = 400 Ω, C= 5.0 μ F, y L = 0.50 H,
encuentre la corriente máxima y la potencia promedio disipada en
el circuito.
XL = ωL
1
C
XC
ω
=

58. Un resistor de 80 Ω, un inductor de 200 mH y un capacitor de 0.150 μF se conectan en
paralelo a través de una fuente de 120 V (rms) que opera a 374 rad/s. a) Calcule la
corriente rms en el resistor, inductor y capacitor b) Cuál es la corriente rms entregada
por la fuente , c) Cuál es la frecuencia resonante del circuito

59. Hallar la corriente máxima y el ángulo de
desfase.
Hallar también la potencia media
suministrada por la f.em.
Datos: Vo = 100 V, R= 1 Ω, L=0.003 H, C=0.002
F, ω=120π rad/s
a
c
biL iC
iR
Nodo b
LCR
iiii +==0
( )CVi bcC
ω=






=
L
Vi bcL
ω
1






−=
L
CVi bc
ω
ω
1
0
L
VCVi bcbc
ω
ω
1
0
−=






==
C
iXiV CCCC
ω
1
( )LiXiV LLLL ω==

60. i0
222
0 bcab
VVV +=Fasores se suman
como vectores
2
2
022
0
2
0
1






−
+=
L
C
i
RiV
ω
ω


















−
+= 2
22
0
2
0
1
1
L
C
RiV
ω
ω 

















−
+
=
2
2
0
0
1
1
L
C
R
V
i
ω
ω
φcos
2
1
VIP =R
Z
IR
IZ
V
V
ab
bc
===φtan
R
L
C 





−
=
ω
ω
φ
1
tan

62. PROBLEMA
En la figura R1 = 60.0 Ω, R2 = 40.0 Ω, L= 0.400 H, C = 5.00 µF y Vrms =240 V.
¿Cuál es la potencia que suministra la fuente en el límite donde:
a) la frecuencia ω de la fuente es muy grande.
b) ω es muy pequeña.
LXL ω= Si ω ∞→
Entonces XL ∞→ Y la corriente en R1 es
cero.
( )
Ω
==∴
0.40
240
2
2
2
V
R
V
P
rms
WP 1440=
00Si →⇒→ LXω ∞→CXy
La corriente en R2 es cero y
( )
Ω
==
60
240
2
1
2
V
R
V
P
rms
WP 960=

63. PROBLEMA
En cierto circuito L-R-C en serie, R = 300 Ω, L = 0.400 H y C = 6.00x10-8
F.
Cuando la fuente de ca funciona a la frecuencia de operación del circuito, la
amplitud de corriente es de 0.500 A.
a) ¿Cuál es la amplitud del voltaje de la fuente?
b) ¿Cuál es la amplitud de voltaje entre los extremos del resistor, del inductor y
del capacitor?
c) ¿Cuál es la potencia promedio que la fuente suministra?
SOLUCION
a) A la frecuencia de resonancia Z = R
IRIZV == VAV 150300500.0 =Ω×=
VIRVb 150) ==
LXL ω=
C
LXX CL
ω
ω
1
=⇒=
LC
12
=ω LC
1
=ω
LC
L
XL =
C
LXL = Ω=
×
= −
2582
1000.6
400.0
8
H
XL

64. Ω=
×
= −
2582
1000.6
400.0
8
H
XL
Ω×== 2582500.0 AIXV LL
VVL 1291=
C
XC
ω
1
=
C
L
C
LC
XC == Ω= 2582CX VIXV CC 1291==
RIVIPc 2
2
1
cos
2
1
) == φ En resonancia cosΦ = 1
( ) ( )Ω= 300500.0
2
1 2
AP
WP 5.37=
LC
1
=ω

65. EL TRANSFORMADOR
La corriente alterna en el devanado primario establece un campo
magnético variable en el núcleo de hierro. Debido a que el hierro se
magnetiza fácilmente, aumenta en gran medida el campo magnético con
respecto al campo que hay en un núcleo de aire y orienta las líneas de
campo al devanado secundario

66. En un núcleo bien diseñado, casi todo el flujo magnético Φ que pasa a
través de cada vuelta del devanado primario también pasa a través de
cada vuelta del devanado secundario.
Dado que el campo magnético es variable, entonces el flujo a través de
los devanados primario y secundario también es variable y, por
consiguiente, en ambas bobinas se induce una fem.
En la bobina secundaria, la fem inducida surge de la inducción mutua y
está dada por la ley de Faraday de la inducción electromagnética como:
dt
d
NV ss
Φ
−=
En el devanado primario, la fem inducida Vp se debe a la
autoinducción y está especificada por la ley de Faraday como:
dt
d
NV pp
Φ
−= El término
dt
dΦ es el mismo en ambas
ecuaciones

67. Al dividir las ecuaciones anteriores:
p
s
p
s
N
N
V
V
= Esta es la ecuación del transformador
Razón de transformación
Si el interruptor se cierra, entonces en el circuito existe una corriente Is y
se suministra energía eléctrica al calentador.
La potencia media suministrada al devanado primario es igual a la
potencia media suministrada al devanado secundario.
sp PP =
p
s
p
s
s
p
sspp
N
N
V
V
I
I
IVIV ==⇒=

68. EJEMPLO
Un transformador reductor dentro de un receptor estereofónico tiene 330
vueltas en el devanado primario y 25 vueltas en el secundario. La clavija
conecta al primario a un tomacorriente de 120 V, y hay una corriente de
0.83 A en el primario mientras el receptor está encendido. Al devanado
secundario están conectados los circuitos transistores del receptor.
Encuentre:
a)La tensión a través del devanado secundario
b)la corriente en el secundario
c)la potencia eléctrica media suministrada a los circuitos transistores.
p
s
p
s
N
N
V
V
= VV
N
N
VV
p
s
ps 1.9
330
25
120 ===
b)
p
s
s
p
N
N
I
I
= AA
N
N
II
s
p
ps 11
25
330
83.0 ===
c) ( ) ( ) WVAVIP sss 1001.911 =×==
a)