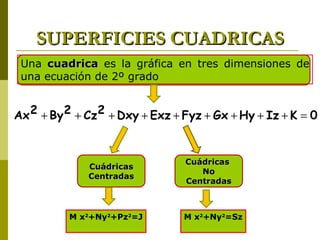
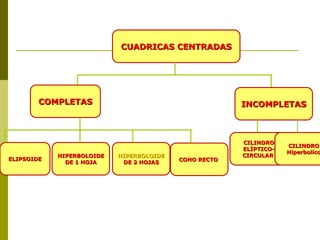
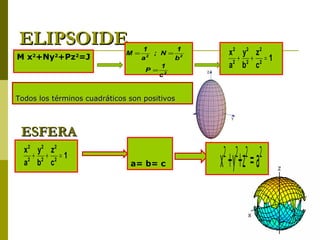
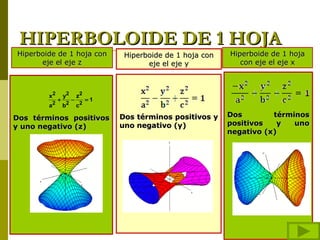
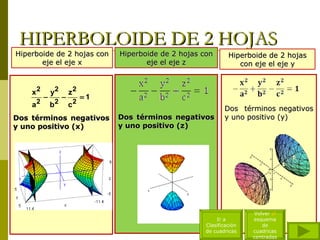
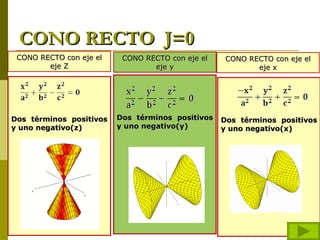
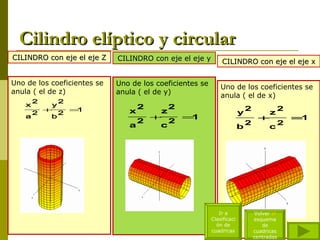
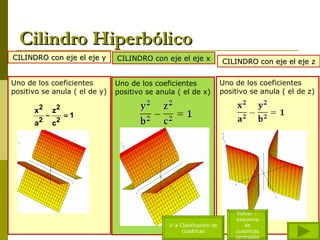
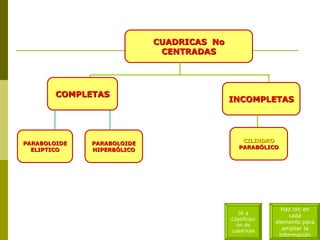
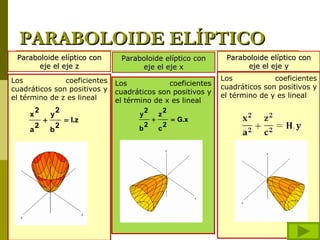
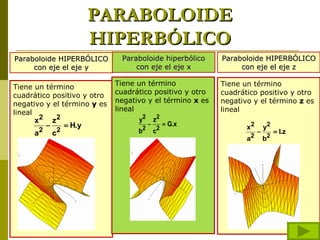
El documento describe diferentes tipos de superficies cuádricas que se presentan comúnmente en obras de arquitectura, incluyendo elipsoides, esferas, hiperboloides de una y dos hojas, cilindros elípticos, paraboloides elípticos e hiperbólicos, y conos rectos. Explica las ecuaciones matemáticas que definen cada tipo de superficie cuadrática y cómo los diferentes términos positivos y negativos dan forma a cada una.

1. LAS CUADRICAS EN
ARQUITECTURA
MARTA LÍA MOLINA
2012

2. Las cuádricas y las obras
arquitectónicas
Las cónicas y cuadricas están
presentes en numerosas obras de
arquitectura, las que iremos
descubriendo a medida que leamos
este material.

3. ELIPSOIDE

4. ESFERA

5. HIPERBOLOIDE
DE UNA HOJA

6. CILINDRO
HIPERBÓLICO

7. PARABOLOIDE HIPERBÓLICO

8. SUPERFICIES CUADRICAS
Una cuadrica es la gráfica en tres dimensiones de
una ecuación de 2º grado
Ax 2 + By 2 + Cz2 + Dxy + Exz + Fyz + Gx + Hy + Iz + K = 0
Cuádricas
Cuádricas
No
Centradas
Centradas
M x2+Ny2+Pz2=J M x2+Ny2=Sz

9. CUADRICAS CENTRADAS
COMPLETAS INCOMPLETAS
CILINDRO
CILINDRO
ELÌPTICO-
Hiperbolico
HIPERBOLOIDE HIPERBOLOIDE CIRCULAR
ELIPSOIDE CONO RECTO
DE 1 HOJA DE 2 HOJAS

10. ELIPSOIDE 1 1
M x2+Ny2+Pz2=J
M= ; N= 2 x 2 y2 z 2
a2 b
2
+ 2+ 2=1
P= 2
1 a b c
c
Todos los términos cuadráticos son positivos
ESFERA
x 2 y2 z 2 2 2 2 2
2
+ 2+ 2=1
a b c a= b= c x +y +z = a

11. HIPERBOLOIDE DE 1 HOJA
Hiperboide de 1 hoja con Hiperboide de 1 hoja con Hiperboide de 1 hoja
eje el eje z eje el eje y con eje el eje x
x2 y2 z2
+ − =1
a2 b2 c2
Dos términos positivos Dos términos positivos y Dos términos
y uno negativo (z) uno negativo (y) positivos y uno
negativo (x)

12. HIPERBOLOIDE DE 2 HOJAS
Hiperboide de 2 hojas con Hiperboide de 2 hojas con Hiperboide de 2 hojas
eje el eje x eje el eje z con eje el eje y
x2 y2 z2
− − =1
a2 b2 c2
Dos términos negativos
Dos términos negativos Dos términos negativos y uno positivo (y)
y uno positivo (x) y uno positivo (z)
Volver al
Ir a esquema
Clasificación de
de cuadricas cuadricas
centradas

13. CONO RECTO J=0
CONO RECTO con eje el CONO RECTO con eje el CONO RECTO con eje el
eje Z eje y eje x
Dos términos positivos Dos términos positivos Dos términos positivos
y uno negativo(z) y uno negativo(y) y uno negativo(x)

14. Cilindro elíptico y circular
CILINDRO con eje el eje Z CILINDRO con eje el eje y CILINDRO con eje el eje x
Uno de los coeficientes se Uno de los coeficientes se Uno de los coeficientes se
anula ( el de z) anula ( el de y) anula ( el de x)
2 2
x y 2 2
+ =1 x z 2 2
2 2 y z
a b + =1 + =1
2 2 2 2
a c b c
Ir a Volver al
Clasificaci esquema
ón de de
cuadricas cuadricas
centradas

15. Cilindro Hiperbólico
CILINDRO con eje el eje y CILINDRO con eje el eje x CILINDRO con eje el eje z
Uno de los coeficientes Uno de los coeficientes Uno de los coeficientes
positivo se anula ( el de y) positivo se anula ( el de x) positivo se anula ( el de z)
x2 z2
− =1
a2 c2
Volver al
esquema
Ir a Clasificación de de
cuadricas cuadricas
centradas

16. CUADRICAS No
CENTRADAS
COMPLETAS
INCOMPLETAS
PARABOLOIDE PARABOLOIDE CILINDRO
ELIPTICO HIPERBÓLICO PARABÒLICO
Haz clic en
IR a
cada
Clasificaci
elemento para
ón de
cuadricas ampliar la
información

17. PARABOLOIDE ELÍPTICO
Paraboloide elíptico con Paraboloide elíptico con Paraboloide elíptico con
eje el eje z eje el eje x eje el eje y
Los coeficientes Los coeficientes
Los coeficientes cuadráticos son positivos y
cuadráticos son positivos y cuadráticos son positivos y
el término de z es lineal el término de y es lineal
el término de x es lineal
2 2 2 2
x y y z
+ = I.z + = G.x
2 2 2 2
a b b c

18. PARABOLOIDE
HIPERBÓLICO
Paraboloide HIPERBÓLICO Paraboloide hiperbólico Paraboloide HIPERBÓLICO
con eje el eje y con eje el eje x con eje el eje z
Tiene un término Tiene un término
Tiene un término
cuadrático positivo y otro cuadrático positivo y otro
cuadrático positivo y otro
negativo y el término x es negativo y el término z es
negativo y el término y es
lineal lineal
lineal
x 2 z2 y2 z2
− = H.y − = G.x x2 y2
a2 c2 b2 c 2 − = I.z
a2 b2

19. CILINDRO PARABÓLICO
Cilindro parabólico
Uno de los coeficientes cuadráticos se anula
2 2 2
Ax = I.z ; B.y = I.z ; C.z = H.y
2 2 2
A .x = H.y ; B.y = G.x ; C.z = G.x