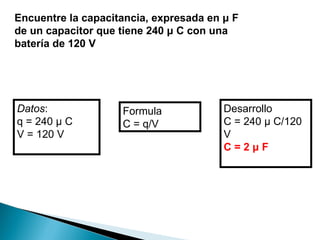
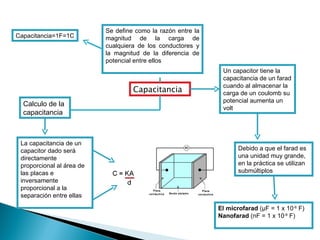
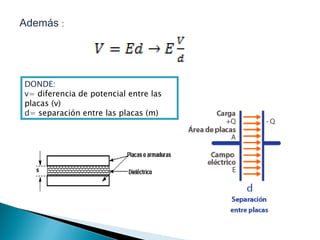
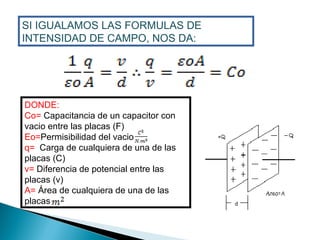
El documento resume los conceptos fundamentales de la capacitancia y cómo se calcula. Explica que la capacitancia de un capacitor depende directamente del área de las placas y de forma inversa a la separación entre ellas. También define la unidad de faradio y los submúltiplos como microfaradio y nanofaradio que se usan en la práctica. Presenta fórmulas para calcular la capacitancia en función de la carga, diferencia de potencial, área y separación de las placas.

1. Maestro : Ing. Ernesto Yáñez Rivera Materia: Física II Equipo: Cortes Peña Jesús Enrique Cruz Guevara Mario Alberto Lajas Aguilar Jesús Ernesto. Vega Salmorán Víctor Manuel Grado/Grupo : 5º “K” CALCULO DE LA CAPACITANCIA

2. Se define como la razón entre la magnitud de la carga de cualquiera de los conductores y la magnitud de la diferencia de potencial entre ellos CAPACITANCIA=1F=1C

3. Es un hecho comprobado que un capacitor formado por un solo conductor puede almacenar una cantidad de carga, pero dos conductores de placas paralelas, pueden almacenar una mayor cantidad. Debido al fenómeno físico de la inducción de dos conductores estrechamente separados

4. La capacitancia de un capacitor dado será directamente proporcional al área de las placas e inversamente proporcional a la separación entre ellas

5. Debido a que el farad es una unidad muy grande, en la práctica se utilizan submúltiplos de ella El microfarad ( μ F = 1 x 10 -6 F) Nanofarad (nF = 1 x 10 -9 F) Por definición: un capacitor tiene la capacitancia de un farad cuando al almacenar la carga de un coulomb su potencial aumenta un volt: Un farad = un coulomb un volt

6. Se a comprobado que para un capacitor con aire o vacio entre sus placas la intensidad del campo esta dada por: E= Donde: q= Carga de cualquiera de las placas (C) A= Área de cualquiera de las placas Eo= Permisibilidad del vacio 8.85x10^-12

7. Además : DONDE: v= diferencia de potencial entre las placas (v) d= separación entre las placas (m)

8. SI IGUALAMOS LAS FORMULAS DE INTENSIDAD DE CAMPO, NOS DA: DONDE: Co= Capacitancia de un capacitor con vacio entre las placas (F) Eo= Permisibilidad del vacio q= Carga de cualquiera de una de las placas (C) v= Diferencia de potencial entre las placas (v) A= Área de cualquiera de una de las placas

9. La constante ε llamada permeabilidad eléctrica o simplemente permisividad del medio aislante, es igual al producto de la constante de permisividad del vacío ε o = 8.85 x 10 -12 C 2 /Nm 2 , y ε r o sea, la permisividad relativa o coeficiente dieléctrico del medio aislante. Por lo tanto: ε = ε o ε r . Los valores de la permitividad relativa o coeficiente dieléctrico ( ε r ) de algunas sustancias aislantes se dan en el cuadro siguiente

10. Permitividad relativa de algunos medios Medio aislador Permitividad relativa ( ε r ) Agua Glicerina Mica Vidrio Aceite Gasolina Aire Vacío 80.5 45 5.6 4.7 2.8 2.35 1.0005 1.0000

11. Condensador de placas paralelas. Un condensador de placas paralelas tiene un área A=2cm²=2X10¯4m² y una separación entre las placas d=1mm = 10¯³m. Encuentre su capacitancia. Solución:

12. Dos láminas cuadradas de estaño de 30 cm de lado están adheridas a las caras opuestas de una lámina de mica de 0.1 mm de espesor con una permitividad relativa de 5.6 ¿cuál es el valor de la capacitancia? Datos Fórmula l = 30 cm = 0.3 m C = ε A d = 0.1 mm d ε r = 5.6 ε o = 8.85 x 10 -12 C 2 /Nm 2 , C= ? Solución: Cálculo de la permitividad ε de la mica: ε = ε o ε r ε = 8.85 x 10 -12 C 2 /Nm 2 x 5.6 = 49.56 x 10 -12 F/m.

13. Cálculo de cualquiera de las dos placas: A = l 2 = (0.3 m) 2 =0.09 m 2 . Conversión de unidades: Como 1 m = 1 x 10 3 mm. 0.1 mm x 1 m =1 x 10 -4 m. 1 x 10 3 mm. Sustitución y resultado: C = 49.56 x 10 -12 F/m.x 0.09 m 2 . 1 x 10 -4 m. C = 446 x 10 -10 F = 0.0446 μ F .

14. Las placas de un capacitor tienen una separación de 5 mm en el aire. Calcular su capacitancia si cada placa rectangular mide 15 cm x 20 cm. Datos d = 5 mm A = 0.15 m x 0.20 m ε r = 1 ε o = 8.85 x 10 -12 C 2 /Nm 2 C = ? Fórmula C = ε A d

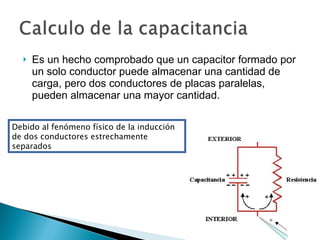
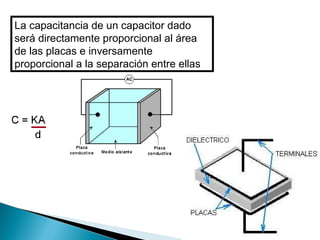
15. Solución: como la permitividad relativa para el aire prácticamente puede ser considerada igual a uno, el valor de la permitividad ε del aire es igual a la permitividad en en vacío ε o, es decir: ε aire = ε o = 8.85 x 10 -12 C 2 /Nm 2 Cálculo del área de una de las placas: A = 0.15 m x 0.20 m = 0.03 m 2 . Conversión de unidades: 5 mm x 1 m = 5 x 10 -3 m 1 x 10 3 mm Sustitución y resultado: C = 8.85 x 10 -12 F/m x 0.03 m 2 . 5 x 10 -3 m C = 5.31 x 10 -11 F = 53.1 pF . [picofarad (pF = 1 x 10 -12 F)]

16. Encuentre la capacitancia, expresada en μ F de un capacitor que tiene 240 μ C con una batería de 120 V Datos : q = 240 μ C V = 120 V Formula C = q/V Desarrollo C = 240 μ C/120 V C = 2 μ F

17. Encuentre la capacitancia, expresada en Faradios, de un capacitor que fue construido pegando una hoja de papel de estaño en ambos lados de una de papel de parafina de área 625 cm ² y de espesor s = 0,0025 cm. Datos : A = 625 cm ² = 6,25.10 -2 m ² s = 0,0025 cm = 2,5.10 -5 m Formula C = Κ.ε 0 . A/s Desarrollo C = 2,1.8,85415.10 -12 (C ²/Nm ²). 6,25.10 -2 m ²/2,5.10 -5 m C = 4,65.10 -8 C ²/Nm C = 4,65.10 -8 F

18. Considere un condensador de placas paralelas, cada una con un área de 0.2m^2 y separadas una distancia 1cm. A este condensador se le aplica una diferencia de potencial V=3000voltios hasta que el condensador se carga, después de lo cual se desconecta de la batería y el condensador queda aislado. Luego se llena el condensador con un material dieléctrico de constante desconocida K , y se observa que el potencial disminuye a V' = 1000 voltios. Calcule: a). La capacitancia C antes de rellenar el condensador con material dieléctrico

19. Capacitancia Se define como la razón entre la magnitud de la carga de cualquiera de los conductores y la magnitud de la diferencia de potencial entre ellos Capacitancia=1F=1C Calculo de la capacitancia La capacitancia de un capacitor dado será directamente proporcional al área de las placas e inversamente proporcional a la separación entre ellas Un capacitor tiene la capacitancia de un farad cuando al almacenar la carga de un coulomb su potencial aumenta un volt Debido a que el farad es una unidad muy grande, en la práctica se utilizan submúltiplos El microfarad ( μ F = 1 x 10 -6 F) Nanofarad (nF = 1 x 10 -9 F)

20. Nuestro equipo llego a la conclusión de que el calculo de la capacitancia es cuando las formulas de intensidad de campo se igualan. Y que La capacitancia de un capacitor dado será directamente proporcional al área de las placas e inversamente proporcional a la separación entre ellas