Este documento presenta los conceptos básicos de cálculos en química, incluyendo el tratamiento de errores experimentales, la expresión de datos con cifras significativas y la notación científica, así como operaciones básicas utilizando factores de conversión. Explica la diferencia entre exactitud y precisión de datos, y cómo propagar las cifras significativas en cálculos algebraicos.

1. Cálculos básicos en química
Química (1S, Grado Biología) UAM Cálculos básicos

2. Contenidos
• Cálculos básicos en química
– Errores: exactitud y precisión
– Expresión de datos: cifras significativas
– Operaciones básicas: factores de conversión
Química (1S, Grado Biología) UAM Cálculos básicos 2

3. Bibliografía recomendada
• Petrucci: Química General, 8ª edición. R. H. Petrucci, W. S. Harwood,
F. G. Herring, (Prentice Hall, Madrid, 2003).
– Secciones 1.6, 1.7, 1.8
Química (1S, Grado Biología) UAM Cálculos básicos 3

4. Datos experimentales: exactitud y precisión
Dos acepciones del término “error experimental”
• Exactitud: grado de proximidad al valor verdadero
– El valor verdadero es desconocido, normalmente
– Pueden conocerse datos más exactos que sirvan de referencia
• Precisión: grado de reproducibilidad de los datos
– Qué valor se obtendrá al hacer una nueva medida con un cierto
montaje experimental
• Rango en el que caerá, p.ej., con una probabilidad del 95%
[Lectura: Petrucci 1.7]
Química (1S, Grado Biología) UAM Cálculos básicos 4

5. Datos experimentales: exactitud y precisión
Tipos de errores según sus fuentes
• Exactitud. Determinada por:
– Errores sistemáticos (fuentes: diseño y montaje experimental)
– Errores personales (fuente: impericia)
• Precisión. Determinada por:
– Errores de escala (fuentes: resolución del instrumental y del diseño)
– Errores accidentales (fuentes: fluctuaciones imprevisibles e
inevitables; impericia)
[Lectura: Petrucci 1.7]
Química (1S, Grado Biología) UAM Cálculos básicos 5

6. xverd  47.2315798421...
Química (1S, Grado Biología) UAM Cálculos básicos 6

7. Inexactas,
imprecisas
x  37  3
xverd  47.2315798421...
Química (1S, Grado Biología) UAM Cálculos básicos 7

8. Inexactas,
más precisas
x  37  2
xverd  47.2315798421...
Química (1S, Grado Biología) UAM Cálculos básicos 8

9. Exactas,
imprecisas
x  46  3
xverd  47.2315798421...
Química (1S, Grado Biología) UAM Cálculos básicos 9

10. Exactas,
más precisas
x  46  2
xverd  47.2315798421...
Química (1S, Grado Biología) UAM Cálculos básicos 10

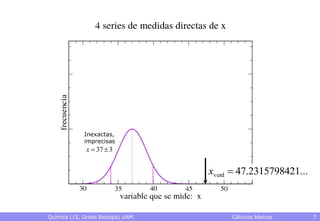
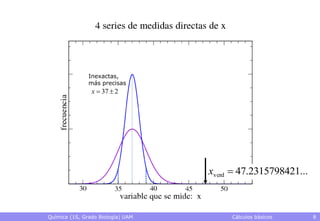
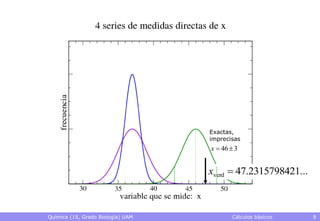
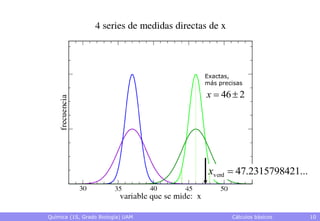
11. Cifras significativas de un dato
V  19,30  0,02  ml
• El uso de cifras significativas (CS) en datos es un modo simplificado
de expresar las imprecisiones de los mismos
• Son significativas las cifras de un dato que tienen valor indicativo de
su precisión o reproducibilidad
– La última CS es imprecisa, aunque no se suele saber cuánto; determina
el centro de la ventana de reproducibilidad
– Las CS anteriores son totalmente precisas
• Número de CS de un dato:
– No cambia al transformar las unidades en que se expresa el dato
19,30 ml = 0,01930 l = 0,00001930 m3
– Los dígitos distintos de 0 son significativos
– Los 0 a la izquierda del primer dígito distinto de 0 no son significativos
– Todos los demás 0 son significativos
Ej.: 0,01930 l tiene 4 CS
– ¡Nótese la diferencia entre escribir un 0 en el límite derecho de un
número decimal y no escribirlo!
[Prob. 1.1] [Lectura: Petrucci 1.8]
Química (1S, Grado Biología) UAM Cálculos básicos 11

12. Cifras significativas de un dato
V  19,30 ml
• Si se escribe V=19,30 ml, ¿qué imprecisión se está suponiendo de
modo implícito?
19,295 ml  V  19,305 ml, imprecisión supuesta: ±0,005 ml
• ¿Y si se escribe V=19,3 ml?
19,25 ml  V  19,35 ml, imprecisión supuesta: ±0,05 ml
• ¿Es lo mismo escribir V=19,30 ml que V=19,3 ml?
[Lectura: Petrucci 1.8]
Química (1S, Grado Biología) UAM Cálculos básicos 12

13. Notación científica de datos numéricos
19,30 ml = 0,01930 l = 0,00001930 m3
1,930 x 101 ml = 1,930 x 10-2 l = 1,930 x 10-5 m3
• Se usa para expresar inequívocamente las cifras significativas y el
orden de magnitud de un dato
• Un número en notación científica consta de
– mantisa (o significando)
• contiene sólo cifras significativas y está formada por todas ellas
• un número real con una parte entera de un solo dígito; p.ej.: 1,930
• no cambia al transformar a múltiplos/submúltiplos del sistema decimal
– exponente
• indica el orden de magnitud del dato (en las unidades correspondientes)
• es la potencia de 10 por la que se multiplica la mantisa para dar el número
[Recomendación: Petrucci ejemplos 1.5,1.6]
Química (1S, Grado Biología) UAM Cálculos básicos 13

14. Cifras significativas de un resultado
g
m  19,30 ml  3, 2  62 g
ml
• El uso de cifras significativas (CS) en operaciones es un modo
simplificado de abordar la propagación de las imprecisiones de los
datos en los cálculos algebraicos.
• Multiplicaciones y divisiones:
– El resultado tiene tantas CS como las del dato que menos CS tiene
• Sumas y restas:
– El resultado tiene tantas cifras DECIMALES como el dato que menos
cifras decimales tiene
18, 212ml  2,312 ml 1, 22 ml  19,30 ml
[Prob. 1.2] [Lectura: Petrucci 1.8]
Química (1S, Grado Biología) UAM Cálculos básicos 14

15. Factores de conversión
• Son factores multiplicativos que se usan para:
– transformar unidades
– transformar propiedades que se relacionan proporcionalmente
• Un factor de conversión es un factor de proporcionalidad entre:
– dos unidades de una misma magnitud
1l 1000 ml 1l
19,30 ml   0, 01930 l
1000 ml 1l 1000 ml
– dos propiedades que se relacionan proporcionalmente
Ej: la densidad (y su inversa), que son la proporcionalidad entre una
masa y el volumen que ocupa
1 ml
3, 2 g 1 ml 62 g   19 ml
3, 2 g
1 ml 3, 2 g
[Lectura: Petrucci 1.6]
Química (1S, Grado Biología) UAM Cálculos básicos 15

16. Factores de conversión. Ejemplos de uso
• Una nanopartícula esférica de oro tiene un diámetro de 21 nm según una
medida realizada con un microscopio de efecto túnel. Si el radio medio de un
átomo de oro se estima en 135 pm, ¿cuántos átomos de oro se puede
estimar que hay en un diámetro de la nanopartícula?
diámetro dela nanopartícula
 número de átomos enun diámetro de nanopartícula
diámetro deun átomo
21 nm 1012 pm
 9  78
2 135 pm 10 nm
• ¿Cuántos mililitros de una disolución acuosa 0.83 M de glucosa hay que
tomar para ingerir 20 g de dicha sustancia? (Masa molar de la glucosa:
180,16)
1 mol glucosa 1000 ml disolución
20 g glucosa    130 ml disolución
180,16 g glucosa 0,83 mol glucosa
[Recomendación: Petrucci ejemplos 1.2-1.4]
Química (1S, Grado Biología) UAM Cálculos básicos 16