El documento describe el modelo del gas de electrones libres en uno, dos y tres dimensiones. Explica cómo se determinan los niveles de energía permitidos, los niveles ocupados a temperatura cero, la energía de Fermi y otras propiedades como la densidad de estados y la energía total del sistema.


![Bibliografía
Universidad Autónoma de Madrid
• The Physical Chemistry of Solids, R. J. Borg and G. J. Dienes,
(Academic Press, San Diego, 1992).
• Solid State Physics, N. W. Ashcroft and N. David Mermin,
(Thomson Learning, 1976). [Caps. 2, 4, 5, 8 y 9]
• Electronic Structure of Materials, A. P. Sutton, (Clarendon
Press, Oxford, 1993).
Química Física del Estado Sólido. El gas de electrones libres. UAM 3](https://image.slidesharecdn.com/qfes-gasdeelectroneslibres-110207085650-phpapp01/85/Quimica-Fisica-del-Estado-Solido-El-gas-de-electrones-libres-3-320.jpg)

![El gas de electrones libres monodimensional:
El modelo
Universidad Autónoma de Madrid
Distribución monodimensional de electrones libres (*) con una densidad electrónica de ,
de Ne electrones por segmento de longitud L.
(*) Cada electrón se mueve
sometido al potencial creado
N e electrones por todos los demás y se
acepta que éste es el mismo
para todos los electrones y
en cualquier punto del
0 L x espacio disponible para
todos los electrones.
2
∂2
− 2
ψ x ( x) = ε xψ x ( x)
2m ∂x
Atención: éstas NO son
[condiciones de contorno
ψ x ( x + L) = ψ x ( x) periódicas (Born-von Karman)]
las condiciones de
periodicidad naturales
equivalen a construir una del cristal; sólo son
“macrored” de periodicidad L condiciones de
contorno “razonables”
Química Física del Estado Sólido. El gas de electrones libres. UAM 5](https://image.slidesharecdn.com/qfes-gasdeelectroneslibres-110207085650-phpapp01/85/Quimica-Fisica-del-Estado-Solido-El-gas-de-electrones-libres-5-320.jpg)
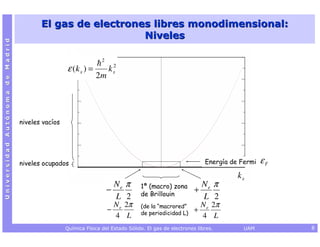
![El gas de electrones libres monodimensional:
Niveles permitidos
Universidad Autónoma de Madrid
2
i kx x i kx x i k′ x
ψ x ( x) = N k ex
; ε (k x ) = k ; 2
x
e e x
′
= 0 si k x ≠ k x ;
2m
cos k x L = 1
c.c. ⇒ e i kx x e i kx L = e i kx x ⇒ e i kxL = 1 ⇒
sen k x L = 0
k x L = 0, ± 2π , ± 4π , = nx 2π
2π k x [ =] L−1
k x = nx (nx = 0, ± 1, ± 2, )
L
Niveles permitidos
2π L
2π 2π 2π 2π 2π
−2 −1 0 1 2 3 kx
L L L L L
Química Física del Estado Sólido. El gas de electrones libres. UAM 6](https://image.slidesharecdn.com/qfes-gasdeelectroneslibres-110207085650-phpapp01/85/Quimica-Fisica-del-Estado-Solido-El-gas-de-electrones-libres-6-320.jpg)


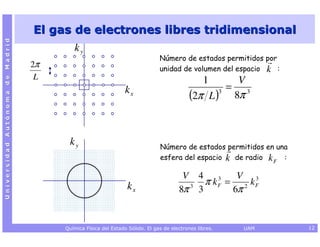
![El gas de electrones libres tridimensional
Universidad Autónoma de Madrid
Distribución tridimensional de electrones libres (*) con una densidad electrónica, de, de
Ne electrones en un volumen V.
2
− ˆ
∇ 2ψ ( r ) = ε ψ (r )
2m
L
[condiciones de contorno periódicas
(Born-von Karman)] L
L
ψ ( x + L, y, z ) = ψ ( x, y, z )
ψ ( x, y + L, z ) = ψ ( x , y , z )
ψ ( x, y , z + L ) = ψ ( x , y , z )
2π 2π 2π
k x = nx k y = ny k z = nz
L L L
(nx = 0, ± 1, ± 2, ) (n y = 0, ± 1, ± 2, ) (nz = 0, ± 1, ± 2, )
2
k ≡ (k x , k y , k z ) ; ψ k (r ) = C e i k r ; ε (k ) = k2
2m
Química Física del Estado Sólido. El gas de electrones libres. UAM 11](https://image.slidesharecdn.com/qfes-gasdeelectroneslibres-110207085650-phpapp01/85/Quimica-Fisica-del-Estado-Solido-El-gas-de-electrones-libres-11-320.jpg)




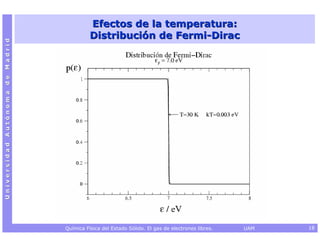
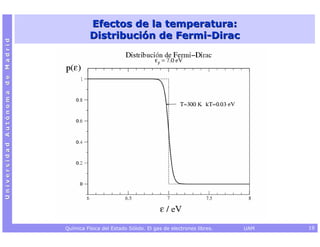
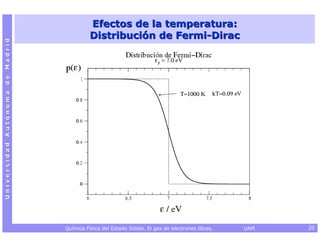
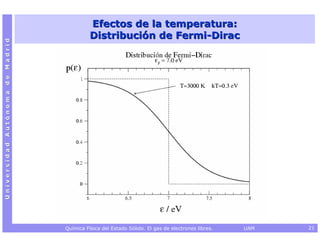
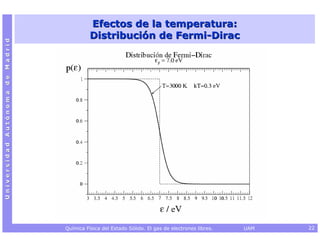

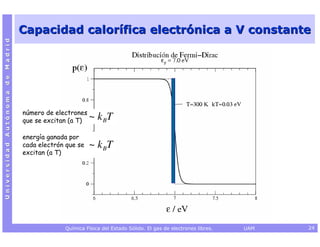
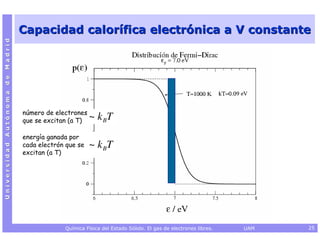
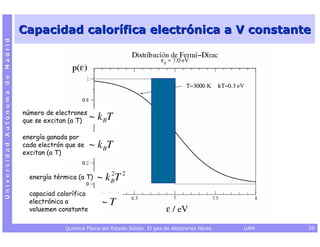
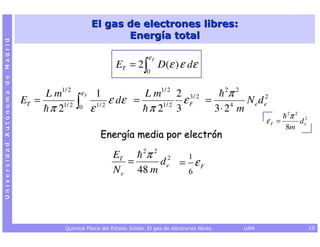
![Capacidad calorífica electrónica a V constante
Universidad Autónoma de Madrid
+∞
por volumen V del metal
(que contiene Ne electrones)
ET = 2 ∫ p (ε ) D (ε ) ε dε
0
+∞ ∂p (ε )
CV ,elec = 2 ∫ D (ε ) ε dε
0 ∂T
∂p (ε ) ε − ε F 1
=
∂T k BT 2 4 cosh 2 [(ε − ε F ) 2k BT ]
+∞ ∂p (ε )
CV ,elec = 2 D (ε F ) ∫ ε dε
0 ∂T
Química Física del Estado Sólido. El gas de electrones libres. UAM 27](https://image.slidesharecdn.com/qfes-gasdeelectroneslibres-110207085650-phpapp01/85/Quimica-Fisica-del-Estado-Solido-El-gas-de-electrones-libres-27-320.jpg)
![Capacidad calorífica electrónica a V constante
Universidad Autónoma de Madrid
+∞ ∂p (ε )
CV ,elec = 2 D (ε F ) ∫ ε dε
0 ∂T
+∞ ε −εF ε
= 2 D (ε F ) ∫ dε
0 k BT 2
4 cosh [(ε − ε F ) 2k BT ]
2
ε −εF
x= ; ε = 2k BT x + ε F ; dε = 2k BT dx
2 k BT
+∞ 2 x ( 2 k BT x + ε F )
= 2 D (ε F ) ∫ εF 2
2k BT dx
−
2 k BT T 4 cosh x
x ( 2 k BT x + ε F )
+∞
CV ,elec = 2 D(ε F ) ∫ 2
k B dx
−∞ cosh x
Química Física del Estado Sólido. El gas de electrones libres. UAM 28](https://image.slidesharecdn.com/qfes-gasdeelectroneslibres-110207085650-phpapp01/85/Quimica-Fisica-del-Estado-Solido-El-gas-de-electrones-libres-28-320.jpg)

