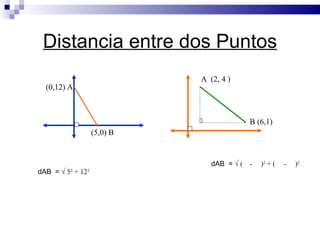
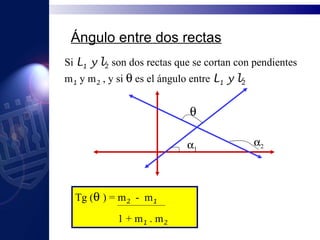
El documento presenta conceptos matemáticos sobre rectas incluyendo la pendiente, ecuaciones de rectas dadas por dos puntos o por punto y pendiente, cálculo de distancias entre puntos y entre rectas paralelas, y ejercicios para determinar pendientes e intersecciones de ecuaciones de rectas.

1. Matemática II Profesor: Jaime Valdivia Palomino pjavaldi

2. H N A R O Z D E

3. Teorema de Pitágoras Cateto ‘a” Cateto ‘b” Hipotenusa ‘c” C 2 = a 2 + b 2 a 2 = c 2 - b 2 b 2 = c 2 - a 2

4. Distancia entre dos Puntos (0,12) A (5,0) B dAB =  5 2 + 12 2 A (2, 4 ) B (6,1) dAB =  ( - ) 2 + ( - ) 2

5. Distancia entre dos Puntos dAB =  ( - ( )) 2 + ( - ( )) 2 dAB = A ( -2, 4 ) A ( X 1 , Y 1 ) B ( 3, -1 ) B ( X 2 , Y 2 )

6. Ecuaciones de la Recta Logro de Sesión: Calcular la ecuación de una recta en diferentes tipos de ejercicios.

7. ¿Qué significan estas señales de tránsito?

8. Pendiente de una recta l ¿Cuál de las rectas está más inclinada? ¿Cómo medimos esa inclinación? L 1 L 2 0 x y

9. Cuando se tienen dos puntos cualesquiera de una recta (x 1 , y 1 ) y (x 2 ,y 2 ), (x 2 , y 2 ) (x 1 , y 1 ) y 2 – y 1 x 2 – x 1 La pendiente queda determinada por el cociente entre la diferencia de las ordenada y la diferencia de las abscisas de los mismos puntos, es decir: m = y 2 – y 1 x 2 – x 1

10. Ejemplo 1 Calcule la pendiente de la recta que pasa por los puntos ( 7 , 2 ) y ( 9 , 14) Identificamos los valores de x 1 , y 1 , x 2 , y 2 x 1 y 1 x 2 y 2 Reemplazamos estos valores en la fórmula m = y 2 – y 1 = x 2 – x 1 14 – 2 9 – 7 = 12 2 = 6

11. Ejemplo 2 Calcule la pendiente de la recta que pasa por los puntos ( -5 , 1 ) y ( 9 , -3) Identificamos los valores de x 1 , y 1 , x 2 , y 2 x 1 y 1 x 2 y 2 Reemplazamos estos valores en la fórmula m = y 2 – y 1 = x 2 – x 1 -3 – 1 9 – (-5) = -4 14 = -2 7

12. Rectas paralelas Dos rectas no verticales l 1 y l 2 cuyas pendientes son m 1 y m 2 , son paralelas ( l 1 // l 2 ) si y sólo si tienen la misma pendiente. Es decir: m 1 = m 2

13. Dos rectas no verticales l 1 y l 2 cuyas pendientes son m 1 y m 2 , son perpendiculares ( l 1  l 2 ) si y sólo si el producto de sus pendientes es -1. Es decir: m 1 . m 2 = -1 Rectas perpendiculares

14. Conclusiones Si m>0 la recta l es creciente Si m<0 la recta l es decreciente Toda recta horizontal tiene m = 0 Las rectas verticales no tienen pendiente definida.

15. Ángulo entre dos rectas Si L 1 y l 2 son dos rectas que se cortan con pendientes m 1 y m 2 , y si  es el ángulo entre L 1 y l 2 Tg (  ) = m 2 - m 1 1 + m 1 . m 2   1  2

16. Ecuación de Recta (Dados 2 puntos ) P (x,y) P 1 (x 1 , y 1 ) P 2 (x 2 , y 2 ) Dado : Punto : P 1 (x 1 , y 1 ) P 2 (x 2 , y 2 ) Pto genérico: P(x, y ) Ec:y – y 1 = m(x – x 1 ) Ec:y – y 1 = Y 2 -Y 1 (x – x 1 ) X 2 - X 1 m = Y 2 -Y 1 X 2 - X 1

17. Ecuación de Recta (Punto - Pendiente ) Dado : Pendiente: m Punto : P 1 (x 1 , y 1 ) Pto genérico: P(x, y ) Ec: y – y 1 = m(x – x 1 ) m 1 P (x,y) P 1 (x 1 , y 2 )

18. Ecuación de Recta (Pendiente e intercepto con el eje de Ordenadas) (0,b) b m 1 P (x,y) Dado : Pendiente: m Intercepto: b Pto genérico: P(x, y ) Ec: y = mx + b

19. DISTANCIA DE UN PUNTO A UNA RECTA

20. DISTANCIA ENTRE RECTAS PARALELAS

21. Ejercicios Determine la pendiente e intersección con y de las siguientes rectas: 4x + 6y +5 = 0 2y = 6 + 3x 3y = 8 – 2x 3y – 2x = 10