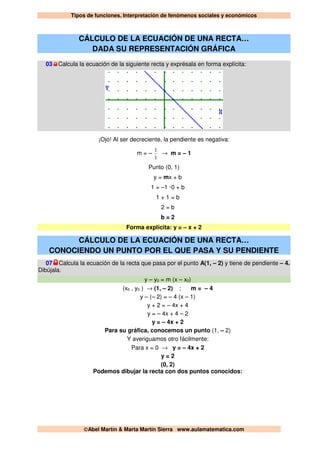
Este documento presenta ejemplos de cómo calcular la ecuación de una recta a partir de diferentes datos. En la primera sección, se muestra cómo calcular la ecuación de una recta decreciente conocido un punto y su pendiente negativa. En la segunda sección, se explica cómo calcular la ecuación de una recta que pasa por un punto dado y tiene una pendiente especificada. Finalmente, se resuelve un ejemplo calculando la ecuación de una recta que pasa por un punto y tiene una pendiente dada en fracción.

1. Tipos de funciones. Interpretación de fenómenos sociales y económicos
©Abel Martín & Marta Martín Sierra www.aulamatematica.com
CÁLCULO DE LA ECUACIÓN DE UNA RECTA…
DADA SU REPRESENTACIÓN GRÁFICA
03 Calcula la ecuación de la siguiente recta y exprésala en forma explícita:
¡Ojo! Al ser decreciente, la pendiente es negativa:
m = –
1
1
→ m = – 1
Punto (0, 1)
y = mx + b
1 = –1 ·0 + b
1 + 1 = b
2 = b
b = 2
Forma explícita: y = – x + 2
CÁLCULO DE LA ECUACIÓN DE UNA RECTA…
CONOCIENDO UN PUNTO POR EL QUE PASA Y SU PENDIENTE
07 Calcula la ecuación de la recta que pasa por el punto A(1, – 2) y tiene de pendiente – 4.
Dibújala.
y – y0 = m (x – x0)
(x0 , y0 ) → (1, – 2) ; m = – 4
y – (– 2) = – 4 (x – 1)
y + 2 = – 4x + 4
y = – 4x + 4 – 2
y = – 4x + 2
Para su gráfica, conocemos un punto (1, – 2)
Y averiguamos otro fácilmente:
Para x = 0 → y = – 4x + 2
y = 2
(0, 2)
Podemos dibujar la recta con dos puntos conocidos:

2. Representación gráfica de las familias de funciones más habituales
Teoría y actividades resueltas
08 Calcula la ecuación de la recta que pasa por el punto A(2, – 3) y tiene de pendiente
–3/2. Dibújala
y – y0 = m (x – x0)
(x0 , y0 ) → (2, – 3) ; m = – 3/2 = – 1.5
y – (– 3) = – 1.5 (x – 2)
y + 3 = – 1.5x + 3
y = – 1.5x + 3 – 3
y = – 1.5x
Para su gráfica, conocemos un punto (2, – 3)
Y averiguamos otro fácilmente:
Para x = 0 → y = – 1.5x
y = 0
(0, 0)
Podemos dibujar la recta con dos puntos conocidos: