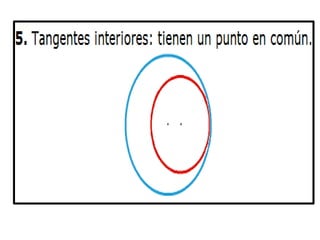
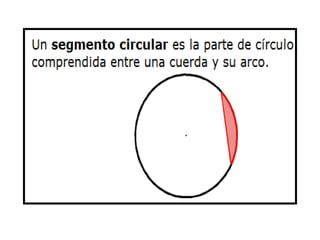
El documento describe las características básicas de las circunferencias y círculos. Explica que una circunferencia es una curva cerrada donde todos los puntos están a igual distancia del centro, y un círculo es el área dentro de una circunferencia. Detalla elementos como el radio, diámetro y arco de una circunferencia, y cómo calcular la longitud de una circunferencia y el área de un círculo.

1. El aro de una canasta de baloncesto y un anillo son circunferencias. La circunferencia es una figura curva, cerrada (no tiene un punto de principio ni de final) y plana (la dibujamos sobre una superficie plana), cuyos puntos están todos a la misma distancia de su centro. Si colocamos el anillo, por ejemplo, sobre una lámina de papel y coloreamos la zona que queda dentro de la circunferencia, esta superficie plana coloreada es un círculo.

2. ELEMENTOS DE LA CIRCUNFERENCIAAlgunos elementos de la circunferencia son: radio, cuerda, diámetro y arco. El radio es el segmento que une cualquier punto de la circunferencia con su centro. Una cuerda es un segmento que une dos puntos de la circunferencia. A la cuerda que pasa por el centro se le llama diámetro. El diámetro mide el doble que el radio, y divide a la circunferencia en dos semicircunferencias. Un arco es la parte de circunferencia comprendida entre dos de sus puntos.

4. LONGITUD DE LA CIRCUNFERENCIALa longitud de una circunferencia es igual a su diámetro multiplicado por el número p (que vale 3,14 y se lee “pi”): Longitud de la circunferencia = diámetro × pSi quisiéramos, por ejemplo, saber lo que avanza la rueda de una bicicleta de 40 cm de diámetro cada vez que da una vuelta, hallaríamos la longitud de su circunferencia: Longitud = 40 × 3,14 = 125,6 cmSi quieres, puedes practicar con el ejemplo siguiente.Si en cada viaje, un tiovivo da 30 vueltas, ¿qué distancia recorrerás si te montas en un caballito que está a 2 metros de su eje o centro?Cada vuelta recorrerás una circunferencia de 2 m de radio; por tanto, su diámetro será: diámetro = 2 × radio = 4 mY la longitud de la circunferencia: longitud = diámetro × 3,14 longitud = 4 × 3,14 = 12,56 mSi en cada viaje se dan 30 vueltas, la distancia recorrida será: 30 × 12,56 = 376,8 m

5. POSICIONES DE UNA RECTA Y UNA CIRCUNFERENCIASobre una superficie plana, una recta y una circunferencia pueden estar en una de estas tres posiciones:1. La recta exterior a la circunferencia: no tienen ningún punto en común.

6. 2. La recta tangente a la circunferencia: tienen un punto en común.

7. 3. La recta secante a la circunferencia: tienen dos puntos en. Común

8. POSICIONES DE DOS CIRCUNFERENCIASDos circunferencias sobre una superficie plana, pueden ocupar distintas posiciones una respecto a la otra, pudiendo ser: exteriores, interiores, concéntricas, tangentes exteriores, tangentes interiores o secantes. 1. Exteriores: no tienen ningún punto en común

14. EL CÍRCULOEl círculo es la figura que forman una circunferencia y su interior. No debes confundir la circunferencia, que es una línea curva, con el círculo, que es la superficie que encierra esa línea.Un sector circular es la parte de círculo comprendida entre dos radios y el arco que abarcan

17. ÁREA DEL CÍRCULOEl área de un círculo de radio R es igual a p por su radio al cuadrado:Área del círculo = p × R2

18. LA CORONA CIRCULARUna corona circular es la zona que queda comprendida entre dos circunferencias de diferentes radios.

19. Para hallar el área de una corona circular, restamos del área del círculo grande el área del círculo pequeño. Siendo R el radio del círculo grande y r el del pequeño, El área será: Área = p × R2 – p × r2