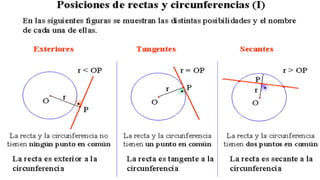
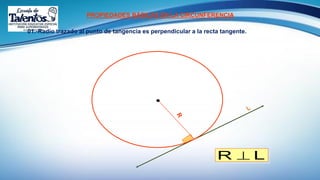
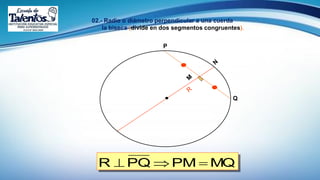
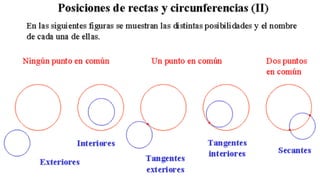
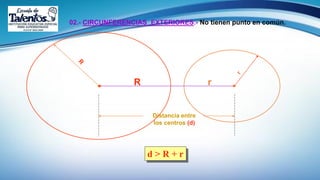
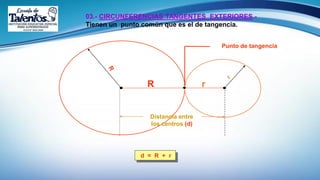
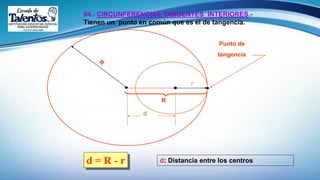
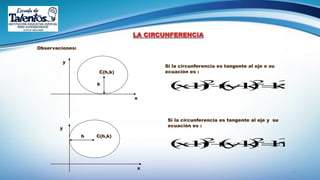
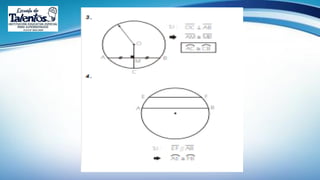
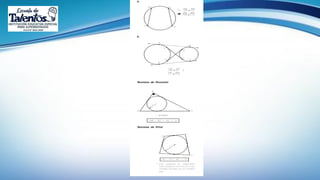
Este documento trata sobre el tema de la circunferencia y sus aplicaciones. Explica conceptos básicos como centro, radio, diámetro y cuerda. Luego presenta ejemplos del uso de la circunferencia en la música, armas, transporte y relojería. Finalmente, proporciona la definición formal de circunferencia y algunas propiedades geométricas como ecuaciones y relaciones entre circunferencias. El documento busca enseñar conceptos básicos de geometría a través de ejemplos prácticos.

1. Circunferencia
Sesión
6
Campo Temático:
• Circunferencia
• Problemas Casuísticos
• Prevención

2. • ¿Recuerda en qué lugares has observado figuras en forma de
circunferencias?
• ¿Qué líneas de la circunferencia conoces?
• ¿Tienen algún parecido estas figuras: una pulsera, un anillo, tapa de goma?
¿A qué formas geométricas se parecen?, ¿Podrán medir todo lo observado?,
¿Qué propiedades de lA círcUNFERENCIA relacionarías con las normas
establecidas por el estado ante el problema del coronavirus?

3. Retroalimentación
REPASO DEL TEMA ANTERIOR
¿Qué aspectos importantes
recordamos del tema de cuadriláteros?
¿Cómo aplico el campo temático
comprendido, ante las relaciones
geométricas?

5. Campo Temático:Sesión 5
Circunferencia
• Circunferencia
• Problemas Casuísticos
• Prevención y Curación

6. Forma Geométrica del Virus Covid 19

7. La Circunferencia en la Música
• Se utilizan técnicas circunferenciales
para muchas cosas.
• Por ejemplo; los Cds, piezas ordinarias
en la música actual, son una placa
circular con un borde que termina
siendo una circunferencia. Al centro
se observa un orificio redondo que
sirve para tomar el Cd y para que la
radio lo reproduzca. Estas piezas de la
electrónica requieren de mucha
precisión para su correcto
funcionamiento.

8. La Circunferencia en las Armas
• El diámetro es un segmento que une
dos puntos de la circunferencia
pasando por el centro, este diámetro
es lo que se usa para medir el tamaño
de agujeros como lo es en las armas.
• Se habla normalmente de pistolas
calibre de 6.35 mm, 7.65 mm, 9 mm,
etc. Esto no es solo un “nombre”, sino
que esto se refiere al tamaño del
agujero (cañón) por donde salen los
proyectiles (balas) del arma, usando el
tamaño del diámetro y usando una
medida milimétrica para lograrlo.

9. La Circunferencia en el Transporte
• En el transporte también podemos
apreciar la presencia de la Circunferencia,
de hecho, donde se puede notar y
ejemplificar mejor es en la Bicicleta, un
conjunto de tubos metálicos con dos
ruedas que aplican la geometría
perfectamente: Las ruedas están hechas
de un “arco”. La mejor parte de esto es
que la rueda se afirma desde el centro y
desde este salen un montón de alambres
delgados llamados “rayos” y estos son
radios que mantienen la forma
circunferencial de la rueda
perfectamente.

10. La Circunferencia en el Sistema Horario
• En la antigüedad todos los relojes eran
de una forma circunferencial.
• El reloj consiste en una placa redonda
(circunferencial) que está dividida en
12 partes iguales, al centro tiene un
agujero por donde sale el sistema del
horario, minutero y segundero. Bueno
evidentemente dentro del reloj se
encuentra todo un sistema de
maquinarias con engranajes y demás
es, pero me centraré en otros
aspectos. Para dividir la circunferencia
en 12 partes exactamente iguales, que
a futuro podrán dar una medición

11. 11
LA CIRCUNFERENCIA
DEFINICION: La Circunferencia es el lugar geométrico del conjunto de puntos en el plano tal que la
distancia de un punto fijo a cada uno de ellos es una constante.
Centro (C) : Punto fijo
radio r : distancia constante
d(P , C) = r
C(h,k)
P(x,y)

12. 12
LA CIRCUNFERENCIA
ELEMENTOS DE LA CIRCUNFERENCIA
C
E
D
F
A B
LT
LN
1. Centro de la circunferencia. “ C “
2. Radio de la circunferencia “ r “
3. Diámetro de la circunferencia
4. Cuerda de la circunferencia
5. Recta tangente a la circunferencia. LT
6. Recta normal a la circunferencia. LN
AB
FD

14. PROPIEDADES BÁSICAS EN LA CIRCUNFERENCIA
01.-Radio trazado al punto de tangencia es perpendicular a la recta tangente.
LR 

15. 02.- Radio o diámetro perpendicular a una cuerda
la biseca (divide en dos segmentos congruentes).
P
Q
MQPMPQR 

17. Distancia entre
los centros (d)
02.- CIRCUNFERENCIAS EXTERIORES.- No tienen punto en común.
d > R + r
R r

18. d = R + r
03.- CIRCUNFERENCIAS TANGENTES EXTERIORES.-
Tienen un punto común que es el de tangencia.
R r
Punto de tangencia
Distancia entre
los centros (d)

19. d
d = R - r
04.- CIRCUNFERENCIAS TANGENTES INTERIORES.-
Tienen un punto en común que es el de tangencia.
d: Distancia entre los centros
R
r
Punto de
tangencia

20. 07.- CIRCUNFERENCIAS INTERIORES.-
No tienen puntos comunes.
d
d < R - r d: Distancia entre los centros

21. 21
LA CIRCUNFERENCIA
Una Circunferencia queda completamente definida, si se conoce su centro y su radio.
Ecuaciones de la Circunferencia:
1) Forma Ordinaria:
Sea el Centro de la Circunferencia
C ( h,k ) y radio r .
Si P (x,y) es un punto 
Por distancia:
2) Forma canónica
si el Centro es el origen su ecuación es :
C(h,k)
P(x,y)
0 X
Y
rPC 
rk)(yh)(x 22

(x - h)2 + (y - k)2 = r2
222
ryx  0
P(x,y)
X
Y

22. 22
LA CIRCUNFERENCIA
Ejemplo 1. Escribir la ecuación de la circunferencia de centro C(-3 , -4) y radio 5.
Solución.
    222
rkyhx 
    254y3x 22

Ejemplo 2. Los extremos de un diámetro de una circunferencia son los puntos A (2 , 3)
y B(-4 , 5). Hallar la ecuación de la curva.
Solución.
C
Las coordenadas del centro :
   
    104y1x
104312ACr
4),1C()
2
53
,
2
42
C(
22
22




y
x
B
A

23. 23
LA CIRCUNFERENCIA
Observaciones:
    222
kkyhx 
C(h,k)
Si la circunferencia es tangente al eje x su
ecuación es :
x
y
k
x
y
C(h,k)h
Si la circunferencia es tangente al eje y su
ecuación es :
    222
hkyhx 

24. 24
LA CIRCUNFERENCIA
3) Ecuación General
Desarrollando la ecuación ordinaria de la circunferencia tenemos:





 
2
,
2
D-
CCentroSu
E
4FED
2
1
r
4
E
4
D
-Fr
4
E
4
D
-F
2
E
y
2
D
x
4
E
4
D
F-
2
E
Eyy
2
D
Dxx
0FEyDxyx
22
22
2
2222
222
2
2
2
22














































Completando cuadrados lo llevamos a su forma ordinaria
Esta ecuación tiene la misma forma que:
Se llama forma general de la circunferencia.

)......0rkh2ky2hxyx
rk2yyh2xhxrkyhx
22222
22222222


x2 + y2 + Dx + Ey + F = 0

25. 25
LA CIRCUNFERENCIA
Ejemplo 3. Reduciendo las ecuaciones dadas a la forma ordinaria , determinar si
representa o no una circunferencia.
a. 2x2 + 2y2 - 6x +10y + 7 = 0
b. 4x2 + 4y2 +28x - 8y + 53 = 0
c. 16x2 + 16y2 - 64x + 8y + 177 = 0
Solución.
- Si D2 + E2 - 4F > 0 ; la Circunferencia es real
- Si D2 + E2 - 4F < 0 ; la Circunferencia es imaginaria
- Si D2 + E2 - 4F = 0 ; la Circunferencia representa un punto
4FED
2
1
r 22
 




 
2
,
2
D-
CCentroSu
E

26. 26
LA CIRCUNFERENCIA
Luego la ecuación es una circunferencia
de centro C (3/2 , -5/2) y radio 5
5
2
5
y
2
3
x
5
4
25
4
9
2
7
2
5
5yy
2
3
3x-x
0
2
7
5y3xyx
0710y6x2y2xa.
22
2
2
2
2
22
22















































36. Investiguemos
en clase:

37. Desarrollo del Campo temático

38. • Ana se ha montado en el caballo que
está a 3.5 m del centro de una
plataforma que gira y su amiga Laura se
ha montado en el león que estaba a 2 m
del centro.
• Calcular el camino recorrido por cada
una cuando la plataforma ha dado 50
vueltas.

39. • Tenemos dos puntos, A y B, y dos
caminos diferentes para ir de uno a
otro.
• El camino de color azul va
directamente de A a B, y el de color
rojo lo hace a través de trayectos
parciales (de A a C, de C a D, de D a
E y, finalmente, de E a B).
• Si todos los caminos son
semicircunferencias ¿qué camino
es más largo, el azul o el rojo?

40. • Una cuerda está enrollada de forma
simétrica alrededor de una barra
circular. La cuerda da la vuelta
exactamente cuatro veces alrededor de
la barra, que tiene una circunferencia
de 4 centímetros y una longitud de 12
centímetros.
• Averigua ¿cuánto mide la cuerda?.
Figura 2

41. Prevención

42. QUÉDATE EN CASA
SALVA VIDAS.
• Ayuda a frenar el coronavirus
• 1. QUÉDATE en casa lo máximo posible
• 2. MANTÉN el distanciamiento social
• 3. LÁVATE las manos con frecuencia
• 4. TOSE cubriéndote con el codo
• 5. LLAMA si tienes síntomas

43. Metacognición
• ¿ Qué comprendí?
• ¿Cuál es su opinión sobre el
campo temático tratado?
• ¿Cómo describiría Ud. el
significado de la circunferencia
cronológica?
• ¿Cómo aplicaría Ud. en su práctica
directiva, el campo temático que
ha comprendido?

44. Emprendimiento
• ¿Cómo aplicaría Ud. en la vida
diaria, los conceptos de la
circunferencia?.
• Si desea innovar alguno de los
productos mostrados. ¿Cuál seria
su propuesta?

45. Recursos Títulos
Libros de Lecturas Links
PDF Enciclopedia Virtual
PDFs
Link
Recursos a utilizar

46. GRACIAS