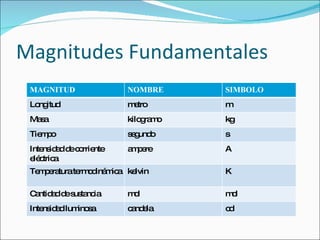
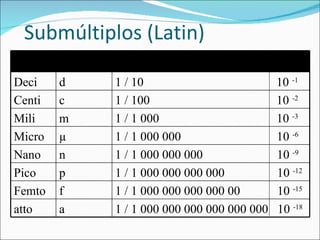
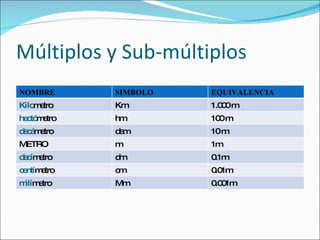
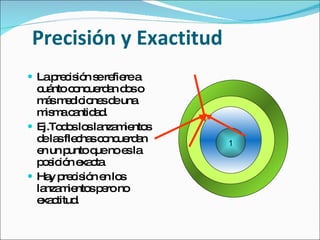
El documento resume los conceptos básicos del Sistema Internacional de Unidades (SI), incluyendo las unidades fundamentales de longitud, masa, tiempo y otras magnitudes. Explica las unidades métricas comunes, factores de conversión, equivalencias entre unidades y la importancia de considerar las cifras significativas en cálculos.

2. Nuestros antepasados medían el tiempo con el sol y la luna

4. Cerca - lejos Rápido Lento Pesado Liviano Silencio - Ruido Frío - caliente

5. Mediciones Fundamentales El Sistema Internacional de unidades (S.I.), es el nombre que recibe el sistema de unidades que utilizan la mayoría de países actualmente. El S.I. se basa en el sistema decimal, distinto del Sistema anglosajón que utiliza fracciones. Las magnitudes pueden ser de dos clases: Fundamentales y Derivadas.

6. Mediciones Fundamentales Magnitudes Fundamentales: aquellas que no dependen de otras unidades como masa en Kilogramos o longitud en metros. Magnitudes Derivadas: dependen de la intervención de dos o más unidades como: d, F. ¿Qué es medir? Determinar alguna magnitud (masa, longitud, etc) comparándola con una unidad de medida, por ejemplo metros, kilogramos, etc.

7. Magnitudes Derivadas Se definen a partir de otras unidades v FUERZA

8. Magnitudes Derivadas Magnitud Nombre Símbolo Relación con unidades básicas Superficie metro cuadrado m 2 m 2 Volumen metro cúbico m 3 m 3 Velocidad metro por segundo m/s m/s Aceleración metro por segundo cuadrado m/s 2 m/s 2 Velocidad angular radián por segundo rad/s s -1 Fuerza Newton N Kg.m/s 2 Presión Pascal Pa N/m Energía/ Trabajo Joule J N.m Entropía Joule por kelvin J/K J/K Intensidad de campo eléctrico Volt por metro V/m V/m

9. Magnitudes Fundamentales MAGNITUD NOMBRE SIMBOLO Longitud metro m Masa kilogramo kg Tiempo segundo s Intensidad de corriente eléctrica ampere A Temperatura termodinámica kelvin K Cantidad de sustancia mol mol Intensidad luminosa candela cd

10. Múltiplos (letras Griegas) Prefijo Símbolo Factor de multiplicación Deca Da 10 10 1 Hecto h 100 10 2 Kilo k 1 000 10 3 Mega M 1 000 000 10 6 Giga G 1 000 000 000 10 9 Tera T 1 000 000 000 000 10 12 Peta P 1 000 000 000 000 000 10 15 Exa E 1 000 000 000 000 000 000 10 18

11. Submúltiplos (Latin) Prefijo Símbolo Factor de multiplicación Deci d 1 / 10 10 -1 Centi c 1 / 100 10 -2 Mili m 1 / 1 000 10 -3 Micro µ 1 / 1 000 000 10 -6 Nano n 1 / 1 000 000 000 10 -9 Pico p 1 / 1 000 000 000 000 10 -12 Femto f 1 / 1 000 000 000 000 00 10 -15 atto a 1 / 1 000 000 000 000 000 000 10 -18

12. Longitud La unidad del S.I. básica de longitud es el Metro (m). La longitud es la distancia que hay entre dos puntos. Las unidades más grandes que el metro se conocen como múltiplos y las unidades más pequeñas que el metro se conocen como submúltiplos. A continuación podemos observar las Unidades métricas comunes:

13. Múltiplos y Sub-múltiplos NOMBRE SIMBOLO EQUIVALENCIA Kilo metro Km 1.000 m hectó metro hm 100 m decá metro dam 10 m METRO m 1m decí metro dm 0.1m centí metro cm 0.01m milí metro Mm 0.001m

14. Longitud Las unidades métricas de la longitud que más se utilizan son el metro, decímetro, centímetro y milímetro. Para transformar las unidades de medidas que se nos presentan debemos multiplicar o dividir por 10, como podemos observar en el siguiente gráfico.

15. Longitud

16. Ejemplos 5 cm = 5 × 10 −2 m = 5 × 0,01 m = 0,05 m Trasformar 1.5 Km ----------------- m 1 Km----------------10 3 m 1.5Km----------------- x x= 1.5. 10 3 m /1km x= 1500 m Como la reducción es de mayor a menor, se multiplica

17. Ejemplos 45 kiló metros = 45 x 1000 metros = 45 000 m 640 µ A = 640 x 1 = 0,00064 A 1 000 000 357,29 mili metros = 357,29 x 1 = 0,357 m 1 000

18. 2.- Trasformar 564 cm ----------------- m 1cm-----------1x10 -2 m x= 564cm-------------X x= 5,65

19. Masa La unidad S.I. básica de masa es el Kilogramo (Kg), que es igual a 1000 g. Igual que en las medidas de longitud, en las de masa también existen múltiplos para las unidades mayores que el gramo y submúltiplos para las unidades menores que el gramo.

20. Múltiplos y Submúltiplos NOMBRE SIMBOLO EQUIVALENCIA Kilogramo Kg 1.000 g hectogramo hg 100 g decagramo dag 10 g gramo g 1 g decigramo dg 0.1 g centigramo cg 0.01 g milígramo mg 0.001 g

21. Masa

22. Ejemplos Trasformar 12 g------------ mg mayor a menor (directo) 1g------------ 10 -3 mg 12g---------------x x=

23. Ejemplo Trasformar 120 k g------------ dg mayor a menor ( dos pasos) 1 kg-----------10 3 g X = 120 Kg-----------x x=120.10 3 g Luego, 1 dg-----------------10 -1 g x= 120.10 4 dg X------------------- 120.10 3 g

24. Volumen Medidas de Volumen: Al hablar del volumen que ocupa un líquido, fluido, gas o sólido, nos referimos al espacio que éstos utilizan Al hablar de volúmenes de sólidos las unidades más utilizadas son el metro cúbico y el centímetro cúbico Se acostumbra utilizar las unidades de medidas para líquidos: el Litro (L), Mililitro (ml), conocido también como cm 3

25. Equivalencias de volumen Volumen = largo x ancho x alto = long x long x long 1 metro cúbico (m 3 ) < > 1 000 000 cm 3 1 litro (l) < > 1000 cm 3 1 metro cúbico (m 3 ) < > 1 000 litros (l)

26. Ejemplos Trasformar 12 km 3 ------------ mm 3 mayor a menor 1km 3 ------------ 10 9 m 3 x= 12km 3 --------------x Trasformar 12.10 9 km 3 ------------ mm 3 mayor a menor 1 m 3 -----------10 -9 mm 3 x = x=12 mm 3 -----------x x= 12 mm 3

27. FACTORES DE CONVERSIÓN El factor de conversión se trata de una fracción que nos permitirá resolver problemas que tienen diferentes unidades pero con la misma magnitud. Por ejemplo si la magnitud es la Masa, pero el problemas se trata de gramos y kilogramos. Cantidad conocida y unidad(es) x Factor(es) de conversión = Cantidad en las unidades deseadas.

28. Otras equivalencias de longitud 1 pulgada (in) < > 25,4 milímetros (mm) 1 pie (ft) < > 0,3048 metros (m) 1 yarda (yd) < > 0,914 metros (m) 1 milla (mi) < > 1,61 kilómetros 1 metro (m) < > 39,37 pulgadas (in) 1 femtómetro (fm) < > 10 –15 metros (m)

29. Ejemplos: pasar 15 pulgadas a cm (factor de conversión: 1 pulgade (in) = 2,54 cm) 15 in × (2,54 cm / 1 in) = 15 × 2,54 cm = 38,1 cm pasar 25 m por s a km por h (factores de conversión: 1 km = 1000 ms, 1 h = 3600 s) 25 m/s × (1 km / 1000 m ) × (3600 s / 1 h) = 90 km/h 3. Ejemplo 3: obtener la masa de 10 litros de mercurio ( densidad del mercurio: 13,6 kilogramos por decímetro cúbico ) Nótese que un litro es lo mismo que un decímetro cúbico. 10 litros de mercurio × (1 decímetro cúbico de mercurio / 1 litro de mercurio) × (13,6 kilogramos / 1 decímetro cúbico de mercurio) = 136 kg

30. Equivalencias de masa 1 kilogramo (kg) < > 1 000 gramos (g) 1 tonelada (ton) < > 1000 kilogramos (kg) 1 slug < > 14,6 kilogramos(kg)

31. Equivalencias de tiempo 1 año < > 365,25 días 1 día < > 24 horas (hr) 1 hora (hr) < > 60 minutos (min) 1 minuto (min) < > 60 segundos (s) 1 hora (hr) < > 3 600 segundos (s) 1 día < > 86 400 segundos (s) 1 año < > 31 557 600 segundos (s)

32. Incertidumbre de Mediciones Ninguna medición es exacta al 100% Precisión se refiere a la cercanía de una serie de medidas entre si. Exactitud se refiere a que tan cerca del valor real se encuentra el valor medido. Dicho de otra manera exactitud tiene que ver con el grado de coincidencia de las mediciones con el valor verdadero.

33. Precisión y Exactitud La precisión se refiere a cuánto concuerdan dos o más mediciones de una misma cantidad. Ej.Todos los lanzamientos de las flechas concuerdan en un punto que no es la posición exacta Hay precisión en los lanzamientos pero no exactitud. 1

34. Precisión y Exactitud La exactitud indica cuán cerca está una medición del valor real de la cantidad medida. Ej.Todas las flechas alcanzan el centro que es la posición exacta de los lanzamientos.. Hay exactitud y precisión en el lanzamiento 1

35. Precisión y Exactitud Vamos a ver un ejemplo para explicar estos conceptos: Supongase que solicitamos a tres estudiantes determinar la masa de un cilindro de aluminio cuya masa real es de 3.00 g. ( ver la gráfica siguiente)

36. Mediciones fundamentales ESTUDIANTE # 1 ESTUDIANTE # 2 ESTUDIANTE # 3 2.65 2.87 3.01 2.76 2.86 3.00 2.68 2.87 2.99

37. Precisión y Exactitud La tabla anterior muestra los resultados de los estudiantes Los resultados de la medición del estudiante #2 son más precisos que los del estudiante #1. Pero ningunos de los resultados del estudiante #1 y #2 es muy exacto. Los resultados del estudiante # 3 no sólo son precisos sino también son lo más exactos.

38. Cifras Significativas (Reglas) 1. Todos los enteros diferentes de cero son significativos. 2. Todos los ceros a la izquierda del (o que preceden al) primer dígito diferente de cero no son significativos. 0,00567 (3) 0,0089 (2) 3. Todos los ceros situados entre dígitos diferentes de cero son significativos. 207,08 (5) 0,0401 (3) 4. Todos los ceros al final de un número con punto decimal son significativos 34,070 (5) 0,0670 (3) 400,00 (3)

39. Ejemplo:Cálculos con cifras significativas En la multiplicación y división el número resultante no tiene más cifras significativas que el número menor de cifras significativas usadas en la operación. Ejemplo: ¿Cuál es el área de un rectángulo de 1,23 cm de ancho por 12,34 cm de largo?. La calculadora nos da 15,1783 cm 2 pero como el ancho sólo tiene tres cifras significativas escribiremos 15,2 cm 2 .