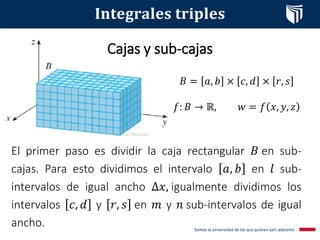
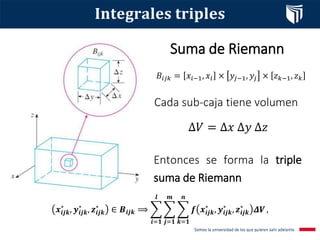
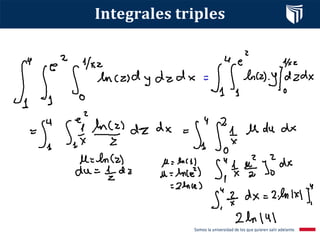
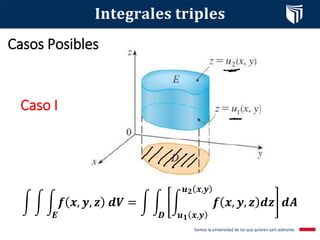
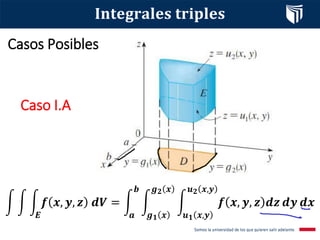
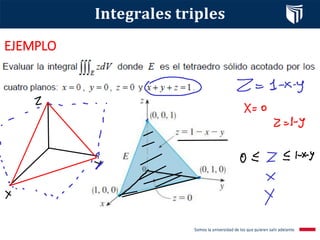
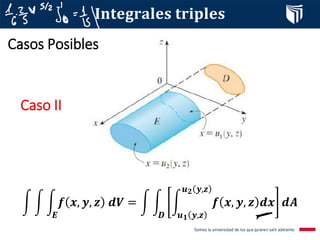
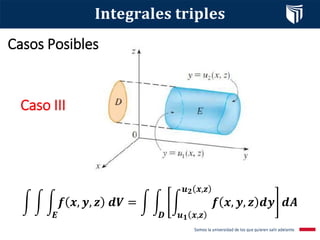
Este documento presenta el tema de integrales triples. Define las integrales triples como una extensión de las integrales dobles para funciones de tres variables, y explica cómo se calculan los volúmenes de sólidos utilizando esta herramienta. También cubre conceptos clave como la suma de Riemann, el teorema de Fubini y diferentes casos posibles para la evaluación de integrales triples. Finalmente, incluye un ejemplo resuelto.