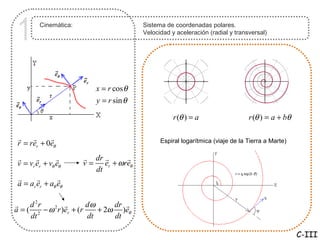
El documento describe los conceptos de cinemática en coordenadas polares, incluyendo velocidad, aceleración radial y transversal. Explica que la aceleración cuantifica la variación de la velocidad en la dirección radial o angular, y que la aceleración de Coriolis ocurre cuando hay variación en la velocidad angular. Finalmente, analiza casos particulares como movimiento circular uniforme, donde la aceleración tangencial es cero y la normal es la aceleración centrípeta.

1. 1 Cinemática: Sistema de coordenadas polares.
Velocidad y aceleración (radial y transversal)
x = r cos θ
y = r sin θ
r (θ ) = a r (θ ) = a + bθ
r r r Espiral logarítmica (viaje de la Tierra a Marte)
r = rer + 0eθ
r r r r dr r r
v = vr er + vθ eθ v = er + ω reθ
dt
r r r
a = ar er + aθ eθ
r d 2r r dω dr r
a = ( 2 − ω 2 r )er + (r + 2ω )eθ
dt dt dt
C-III

2. 2 Aceleración en coordenadas polares.
r
r dv
d 2r Cuantifica la variación de la a=
dt
dt 2 celeridad en la dirección radial
r r
der r deθ r
= ω eθ = −ω er
−ω 2 r Aceleración centrípeta dt dt
dω r d 2r r dω dr r
α= Aceleración angular. Cuantifica a = ( 2 − ω 2 r )er + (r + 2ω )eθ
dt la variación de la vel angular dt dt dt
dr
2ω = 2vω Aceleración de Coriolis
dt
C-III

3. 3 Casos particulares:
r dr r r
Movimiento en 1D
Movimiento circular
v = er + ω reθ r d 2r r dω dr r
dt a = ( 2 − ω 2 r )er + (r + 2ω )eθ
dt dt dt
dθ dθ
Movimiento en 1D ω= =0 Movimiento en 1D
ω= =0
dt dt
2
r dr r r d rr
v = er a = 2 er
dt dt
Movimiento circular r = cte Movimiento circular r = cte
r r dω r dω dv
r a = −ω 2 rer + r eθ aθ = at = r =
v = vθ = ω r dt dt dt
• Aceleración normal en la dir. radial
v2
an = − ar = ω r =
2
r
Movimiento circular uniforme r = cte ω = cte
r
• Aceleración tangencial = 0 a = a n = − ar
• Aceleración normal siempre ≠0
C-III

4. 4 Coordenadas polares (dirección radial y transversal)
Coordenadas respecto al movimiento (dirección tangencial y normal)
C-III

5. 3 Coordenadas polares (dirección radial y transversal)
Coordenadas respecto al movimiento (dirección tangencial y normal)

6. 3 Coordenadas polares (dirección radial y transversal)
Coordenadas respecto al movimiento (dirección tangencial y normal)