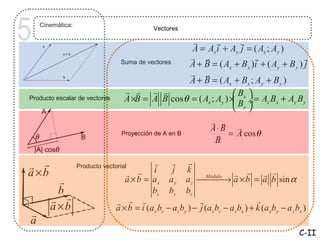
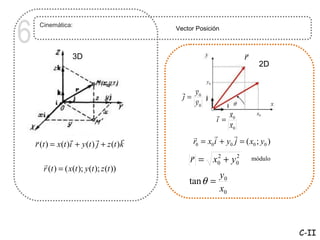
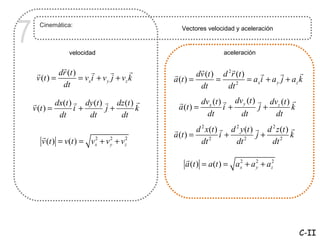
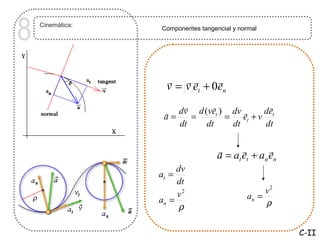
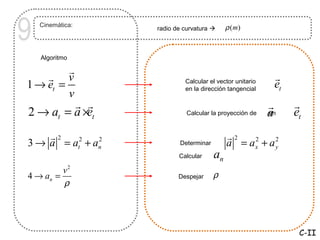
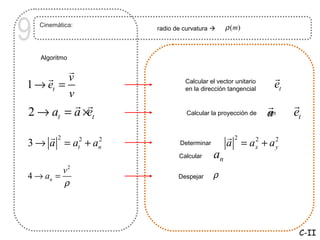
Este documento trata sobre cinemática, que estudia el movimiento de los cuerpos sin considerar las causas. Describe conceptos como sistema de referencia, posición, velocidad, aceleración, vectores y componentes tangenciales y normales. Explica cómo calcular la velocidad, aceleración y radio de curvatura usando derivadas, integrales y álgebra vectorial.

1. 1 Cinemática: Estudia el movimiento de los cuerpos sin tener en cuenta las causas que lo
provocan
Sistema de referencia: Punto material: Movimiento de un cuerpo como
el movimiento solo de un punto material
x0 = 0m x1 = 4m
t0 = 0 s t1 = 2s
x0 = 1m x2 = 9m
t0 = 1s t2 = 3s
Transformaciones de Galileo:
x ′ = x − Vx t
t′ = t
C-I

2. 2 Cinemática:
t
Derivada e integral  Interpretación gráfica
x(t ) = x0 + ∫ v (t )dt
t0
x(t + ∆t ) − x(t ) dx
v(t ) = lim =
∆t →0 ∆t dt
dx
vP = = tan α P
dt
v P > vM
αM αP
C-I

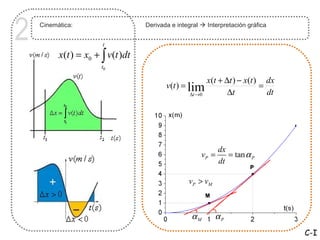
3. 3 Cinemática: Velocidad constante, aceleración constante y variable
Aceleración variable
t
x(t ) = x0 + ∫ v(t )dt
t0
t Unidades
v(t ) = v0 + ∫ a (t )dt
t0 x[m] v[m / s] a[m / s 2 ]
C-I

4. 4 Cinemática: Cinemática en 3D. Vectores posición, velocidad y
aceleración.
Cinemática en 1D. Cinemática en 3D.
r r 2r
dx dv d x 2
r dr r dv d r
v= a= = 2 v= a= = 2
dt dt dt dt dt dt
t t
r r r
x(t ) = x0 + ∫ v(t )dt r (t ) = r0 + ∫ v (t )dt
t0 t0
t t
r r r
v(t ) = v0 + ∫ a (t )dt v (t ) = v0 + ∫ a (t )dt
t0 t0
Unidades
r r r
r [m] v [m / s ] a[m / s 2 ]
C-II

5. 5 Cinemática:
Vectores
r r r
A = Ax i + Ay j = ( Ax ; Ay )
r r r r
Suma de vectores A + B = ( Ax + Bx )i + ( Ay + B y ) j
r r
A + B = ( Ax + Bx ; Ay + B y )
r r r r  Bx 
Producto escalar de vectores A ×B = A B cos θ = ( Ax ; Ay ) × ÷ = Ax Bx + Ay By
 By
 
r r
A⋅ B r
Proyección de A en B r = A cos θ
B
r r Producto vectorial r r r
a ×b r r i j k r r r r
r a × b = ax a y az  a × b = a b sin α
Módulo
→
b bx by bz
r r r r r r r
a ×b a × b = i (a y bz − az by ) − j (a xbz − a z bx ) + k (a xby − a ybx )
r
a
C-II

6. 6 Cinemática:
Vector Posición
r
3D r
2D
y0
r
r y0
j= r
y0
r x0r x0
i = r
x0
r r r r r r
r
r (t ) = x(t )i + y (t ) j + z (t ) k r0 = x0 i + y0 j = ( x0 ; y0 )
r
r r = x0 + y0
2 2 módulo
r (t ) = ( x(t ); y (t ); z (t ))
y0
tan θ =
x0
C-II

7. 7 Cinemática:
velocidad
Vectores velocidad y aceleración
aceleración
r r r r r r
r dr (t ) r dv (t ) d 2 r (t ) r r r
v (t ) = = vx i + v y j + vz k a (t ) = = = ax i + a y j + az k
dt dt dt 2
r dx(t ) r dy (t ) r dz (t ) r r dvx (t ) r dv y (t ) r dvz (t ) r
v (t ) = i+ j+ k a (t ) = i+ j+ k
dt dt dt dt dt dt
r d 2 x(t ) r d 2 y (t ) r d 2 z (t ) r
r a (t ) = i+ j+ k
v (t ) = v(t ) = vx + v y + vz2
2 2
dt 2 dt 2 dt 2
r
a (t ) = a(t ) = ax + a y + az2
2 2
C-II

8. 8 Cinemática:
Componentes tangencial y normal
r rr r
v = v et + 0en
r r r
r dv d (vet ) dv r det
a= = = et + v
dt dt dt dt
r r r
a = at et + an en
dv
at =
dt
v2 v2
ρ an = an =
ρ ρ
C-II

9. 9 Cinemática:
radio de curvatura  ρ ( m)
Algoritmo
r
r v r
1 → et = Calcular el vector unitario
en la dirección tangencial
et
v
r r r r
2 → at = a ×et Calcular la proyección de a
en et
r2 r2
3 → a = at2 + an
2
Determinar a = ax + a y
2 2
Calcular an
v2
4 → an = Despejar ρ
ρ
C-II

10. 9 Cinemática:
radio de curvatura  ρ ( m)
Algoritmo
r
r v r
1 → et = Calcular el vector unitario
en la dirección tangencial
et
v
r r r r
2 → at = a ×et Calcular la proyección de a
en et
r2 r2
3 → a = at2 + an
2
Determinar a = ax + a y
2 2
Calcular an
v2
4 → an = Despejar ρ
ρ
C-II