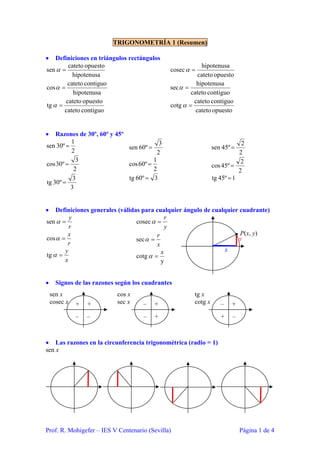
Este documento resume conceptos básicos de trigonometría. Define las funciones trigonométricas en triángulos rectángulos y para cualquier ángulo. Explica las razones trigonométricas para ángulos de 30°, 60° y 45°. Describe las relaciones entre las funciones para ángulos opuestos, suplementarios, complementarios y que difieren en 90° o 180°. Finalmente, presenta fórmulas para resolver triángulos no rectángulos como los teoremas de los senos y cosenos, y otras fórmulas útiles como los teore

1. TRIGONOMETRÍA 1 (Resumen)
• Definiciones en triángulos rectángulos
cateto opuesto hipotenusa
sen α = cosec α =
hipotenusa cateto opuesto
cateto contiguo hipotenusa
cos α = sec α =
hipotenusa cateto contiguo
cateto opuesto cateto contiguo
tg α = cotg α =
cateto contiguo cateto opuesto
• Razones de 30º, 60º y 45º
1 3 2
sen 30º = sen 60º = sen 45º =
2 2 2
3 1 2
cos 30º = cos 60º = cos 45º =
2 2 2
3 tg 60º = 3 tg 45º = 1
tg 30º =
3
• Definiciones generales (válidas para cualquier ángulo de cualquier cuadrante)
y r
sen α = cosec α =
r y
cos α =
x
sec α =
r
y
.
P(x, y)
r x
y x x
tg α = cotg α =
x y
• Signos de las razones según los cuadrantes
sen x cos x tg x
cosec x + + sec x – + cotg x – +
– – – + + –
• Las razones en la circunferencia trigonométrica (radio = 1)
sen x
Prof. R. Mohigefer – IES V Centenario (Sevilla) Página 1 de 4

2. cos x
tg x
• Recorrido
– 1 ≤ sen x ≤ 1 – 1 ≤ cos x ≤ 1 – ∞ < tg x < +∞, ∀x
• Fórmulas fundamentales
1 sen α
1) cotg α = 5) tg α =
tg α cos α
1 cos α
2) sec α = 6) cotg α =
cos α sen α
1 1
3) cosec α = 7) 1 + tg 2α =
sen α cos 2 α
4) sen α + cos 2 α = 1
2
8) 1 + cotg 2α =
1
sen 2α
• Relaciones entre razones de distintos ángulos
Ángulos opuestos: α y – α Ángulos suplementarios: α y 180º–α
α
180 – α α
sen (– α) = – sen α sen (180º – α) = sen α
cos (– α) = cos α cos (180º – α) = – cos α
tg (– α) = – tgα tg (180º – α) = – tgα
–α
Prof. R. Mohigefer – IES V Centenario (Sevilla) Página 2 de 4

3. Áng. que difieren en 180º: α y 180º+α Ángulos complementarios: α y 90º–α
α
α sen (180º +α) = – sen α
90 – α sen (90º – α) = cos α
cos (180º +α) = – cos α
cos (90º – α) = sen α
tg (180º +α) = tg α
tg (90º – α) = cotgα
180º + α
Áng. que difieren en 90º: α y α + 90º
90º+α
sen (90º + α) = cos α
α
cos (90º + α) = – sen α
tg (90º + α) = – cotg α
• Resolución de triángulos no rectángulos
Teorema de los senos
A
a b c
c b = =
sen A sen B sen C
B a C
Observaciones relativas al Teorema de los senos:
1) Sirve para resolver un triángulo conocidos dos ángulos y un lado o dos lados y el
ángulo opuesto a uno de ellos.
2) Cuando se calcula un ángulo hay, en principio, dos soluciones: α y 180º – α.
Hay que comprobar si ambas son válidas: La suma de los tres ángulos no puede
superar 180º, y un triángulo tiene, a lo sumo, un solo ángulo obtuso.
3) Si en un problema determinado podemos optar por aplicar el Teorema de los se-
nos o el Teorema del coseno, hay que elegir siempre el del coseno (porque el de
los senos puede aportar dos soluciones falsamente válidas en estos casos).
Teorema del coseno
A
c b a2 = b2 + c2 – 2 b c cos A
b2 = a2 + c2 – 2 a c cos B
C c2 = a2 + b2 – 2 a b cos C
B a
Observaciones relativas al Teorema del coseno:
1) Sirve para resolver un triángulo conocidos los tres lados o dos lados y el ángulo
comprendido entre ellos.
2) Si en un problema determinado podemos optar por aplicar el Teorema de los se-
nos o el Teorema del coseno, hay que elegir siempre el del coseno (porque el de
los senos puede aportar dos soluciones falsamente válidas en estos casos).
Prof. R. Mohigefer – IES V Centenario (Sevilla) Página 3 de 4

4. • Otras fórmulas útiles
Teorema de Pitágoras
a Sólo en triángulos rectángulos:
c a2 = b2 + c2
b
Teorema de la altura
h Sólo en triángulos rectángulos:
h2 = m·n
m n
Teorema del cateto
c b
Sólo en triángulos rectángulos:
c2 = m·a
m n b2 = n·a
a=m+n
Fórmula de Herón
Calcula el área de un triángulo cualquiera conocidos sus tres lados. Si llamamos p al
perímetro del triángulo, esto es: p = a + b + c, se tiene:
S = p ( p − a )( p − b)( p − c)
Prof. R. Mohigefer – IES V Centenario (Sevilla) Página 4 de 4