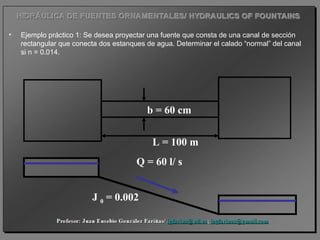
Este documento presenta conceptos clave sobre flujos con superficie libre, incluyendo: el número de Froude, la sección de control, la geometría de la sección transversal, el calado crítico y el calado normal. También define parámetros geométricos como el área mojada, el perímetro mojado y el radio hidráulico para diferentes tipos de secciones. Explica cómo calcular el calado crítico y normal y provee ejemplos numéricos.

1. • 5.1. Introducción.
• 5.2. Número de Froude.
• 5.3. Sección de control del flujo.
• 5.3 Geometría de la sección de una canalización.
• 5.5 Calado crítico.
• 5.6 Calado “normal”.
Tema 5 Fuentes con escorrentía superficial.

2. Caudal:
Q = ∆ V/ ∆ t; Q = [L3
/ T]
Ecuación de continuidad:
Q = A 1v1 = A 2v2 = .....= A nvn
5.1 INTRODUCCIÓN

3. CARACTERÍSTICAS GEOMÉTRICAS DE LA SECCIÓN
TRANSVERSAL DE UN FLUJO CON SUPERFICIE LIBRE
• -Área de la sección de flujo o “área
mojada”, A.
• -Perímetro “mojado”, P.
• -Radio hidráulico, R;
• R = A / P.
• -Ancho superficial, T.
• -Profundidad “hidráulica”, D; D = A/ T.
A
P
T

4. FACTORES DE SECCIÓN
• -Factor de sección “crítico” (Zc
):
• Zc
= (A3
/ T) 0.5
.
• -Factor de sección “normal” (Zn):
• Zn = A R 2/3
.

5. Tipo de
sección
Area,
A
Perímetro
mojado,
P
Radio hidráulico,
R
Ancho superficial,
T
Rectan-
gular
b y b + 2 y b y/ (b+2y) b
Trape-
cial
(b+zy)y b+
2y(1+z2
)0.5
(b+zy)y/
[b+2y(1+z2
)0.5
]
b + 2zy
Trian-
gular
Z y2
2y(1+z2
)0.5
zy/
2(1+z2
)0.5
2 z y
Circular
Parcialmente
llena
(1/8)(θ -
senθ)Do
2
(1/2θ) Do
2
¼(1 – senθ / θ)Do
2(y(Do
-y)0.5

6. Tipo de sección Profundidad
Hidráulica
D
Factor de sección crítico
Zc=A1.5
/ T0.5
Factor de sección normal
Zn=AR2/3
Rectangular y b y 1.5
(by)5/3
[1/(b+2y)]2/3
Trapecial (b+zy)y/
(b+2zy)
[(b+zy)y]1.5
/
(b+2zy)0.5
[(b+zy)y]5/3
/
[b+2y(1+z2
)0.5
]2/3
Triangular 1/2 y 0.7071 z y1.5
Z5/3
y8/3
/
[2(1+z2
) 0.5
]2/3
)
Circular
(Parcialmente
llena)
(1/8)[(θ - senθ)/
sen(1/2)θ] Do
0.0442[(θ – sen θ)1.5
/
(sen(1/2)θ)0.5
] Do
2.5
(1/2)13/3
(θ-sen θ)(1–
(senθ)/θ)2/3
Do
8/3

7. VARIACIÓN DE LAS CARACTERÍSTICAS GEOMÉTRICAS DE SECCIONES
CIRCULARES PARCIALMENTE LLENAS EN FUNCIÓN DE “y”.

8. Ecuación de Bernoulli en conducciones abiertas. Representación gráfica.
H1 = V1
2
/ 2g + y1 + z1 = V2
2
/ 2g + y2 + z2 + hf 1-2 = V3
2
/ 2g + y3 + z3 + hf 1-3
V1
2
/ 2g
y1
z1
1 2 3
V2
2
/ 2g
V3
2
/ 2g
y2
y3
z2
z3
hf 1-3

9. Uniforme (I)
(calado y velocidad constantes)
Clasificación
del flujo
Gradualmente variado (II)
Variado
(calado y
velocidad Rápidamente variado (III)
variables)
CLASIFICACIÓN DEL FLUJO LIBRE
(II)
(III)(I)

10. 5.2 Número de Froude
F = v/ (g*y) 0,5

11. Subcrítico o tranquilo
(F < 1)
Clasificación
del
flujo Supercrítico o rápido
(F > 1)
Crítico
(F = 1)

12. 5.3 SECCIÓN DE CONTROL DEL FLUJO
Es aquella sección en la que se conoce la relación entre el calado
del flujo, o de alguna variable que permite obtenerlo, y el caudal.
3
. cygq =
Sección de control en caída
yc
3
. cygq =
2
3
2. eHgmq =
Sección de control en vertedor
He
P

13. CARACTERÍSTICAS DE LA SECCIÓN DE CALADO CRÍTICO:
- dy / dx =
- F = 1
- El valor del calado crítico (yc) es independiente de la pendiente de fondo del canal. Es
decir, es una propiedad de la sección transversal, del caudal y de g.
Línea de calado crítico
0
0
5.5 CALADO CRÍTICO5.5 CALADO CRÍTICO

14. • Siendo:
De la definición geométrica de Zc:
1≈αRégimen
turbulento
El cálculo de yc se puede realizar resolviendo el sistema de ecuaciones 1 y 2
anteriores o, hallando la raíz “yc”de la ecuación 3:
g
Q
Zc =1
)(
3
c
c
c
c yf
T
A
Z ==
2
g
Q
T
A
yf
c
c
c −=
3
)(3

15. El cálculo del calado crítico para una sección
rectangular simple se reduce a:
3
2
3
2
2
* g
q
bg
Q
yc ==

16. EJEMPLO PRÁCTICO
• Determinar el calado “crítico” de un canal rectangular revestido con cemento
(“n” = 0.013), pendiente de fondo del 2% y 80 cm de ancho, para un caudal de
200 l/ s.
Considere α =1.
• Solución:
• Zc = by 3/2
= 0.8*y 3/2
...................................(1)
• Zc = Q/ g 1/2
= 0.2/ (9.8) 1/2
= 0.064..........(2)
• El valor del calado que satisface que (1) = (2) es:
yc = 18,5 cm

17. 5.6 CALADO NORMAL.

18. • Pendiente de la rasante de pérdidas de carga según Manning-Strickler:
3/42
22
RA
Qn
= 2
22
NZ
Qn
J1
J3
J2
J1 ≠ J2 ≠ J3 ≠ 0
Línea de calado normal
=fJ

19. Tipo de superficie Valores de “n”
Madera cepillada 0.012
Madera sin cepillar 0.013
Mortero de cemento 0.012 a 0.013
Hormigón 0.014 a 0.016
Piedra labrada 0.014 a 0.015
Ladrillo con mortero de cemento 0.013 a 0.016
Grava 0.029
Superficie de cascote 0.030 a 0.033
Superficie de cascote con cemento 0.020 a 0.025
Canalón semicircular metálico y liso 0.012 a 0.013
Canal excavado en roca, liso y uniforme 0.030 a 0.033
Idem, rugoso e irregular 0.040 a 0.045
Tubo de hierro fundido sin recubrir 0.013 a 0.015
Tubo de hierro fundido recubierto 0.012 a 0.013
Tubo de hierro negro, forjado 0.013 a 0.015
Tubo de hierro forjado, galvanizado 0.014 a 0.017
Tubo de acero en espiral 0.015 a 0.017
Tubo vitrificado para alcantarillas 0.013 a 0.017
Tierra 0.020 a 0.025
Tierra con piedras o hierbas 0.033 a 0.040
VALORES DEL COEFICIENTE DE RUGOSIDAD “n”
Ejemplo:
n = 0.014 a 0.016

20. Cálculo del calado
“normal”:
2
1
0
3
2
***
1
JRA
n
Q =
El cálculo de yn se puede realizar resolviendo el sistema de ecuaciones 1 y 2
anteriores o, hallando la raíz “yn”de la ecuación 3:
3
)(* 3
2
nn yfRAZ ==1
0
*
J
nQ
Zn =2
( ) 5.0
0
3
21
)( JAR
n
Qyf hn −=

21. • Ejemplo práctico 1: Se desea proyectar una fuente que consta de una canal de sección
rectangular que conecta dos estanques de agua. Determinar el calado “normal” del canal
si n = 0.014.
Q = 60 l/ s
J 0 = 0.002
b = 60 cm
L = 100 m

22. Respuesta: yn = 0.15 m.

24. Ejemplo práctico 2: Determine el calado normal de circulación en un canal trapezoidal para los
datos siguientes:
Q = 16 m3
/ s, b = 4. 5 m, z1 = 0.50, z2 = 0.70, J0 = 0.0030 y n = 0.030.
2
2
2
1 **5.0**5.0* nnn yzyzybA ++=
)1(*)1(*
2
2
2
1 zyzybP nn ++++=
P
A
R =
0*
)1(*)1(*
**5.0**5.0*
*)**(*
1
2
1
0
3
2
2
2
2
1
2
2
2
12
=
++++
++
+− J
zyzyb
yzyzyb
yzyb
n
Q
nn
nnn
nn
yn es la raíz de la ecuación:

25. 0*
)1(*)1(*
**5.0**5.0*
*)**(*
1
2
1
0
3
2
2
2
2
1
2
2
2
12
=
++++
++
+− J
zyzyb
yzyzyb
yzyb
n
Q
nn
nnn
nn
La raíz de la ecuación yn se puede obtener mediante una calculadora de mano,
hoja electrónica (Maple, Mathcad, etcétera), con una Hoja Excel o similar o
programas como HEC- RAS, FLOWMASTER, etcétera .
Respuesta: yn = 1. 57 m

26. Solución del ejemplo anterior con auxilio de una programación en Hoja Excel:
SECCIONES TRAPECIAL, TRIANGULAR Y RECTANGULAR
AUTOR: Juan E. González Fariñas (jgfarina@ull.es)©
INPUT DATA CELL
DATOS INICIALES: OUTPUT CELL
Q (m
3
/s) 16.00
b (m) 4.50
z1 (adim.) 0.50
z2 (adim.) 0.70
Jo (adim.) 0.0030
"n" Manning (s*pie
- 1/3
) 0.030
PARÁMETROS GEOMÉTRICOS
Z N 8.764 (m
8/3
) y "NORMAL" (m) 1.566 FUNCIÓN OBJETIVO: 0.00
Z c = Q/ g0,5
5.108 (m
2,5
) y "CRÍTICA" (m) 1.037 FUNCIÓN OBJETIVO: 0.00
PARÁMETROS FLUJO "NORMAL"
DN TN AN RHIDRÁULICO PN V"normal" 1.88 (m/s)
(m) (m) (m
2
) (m) (m) Froude 0.52 (adim.) SUBCRÍTICO
1.34 6.38 8.52 1.04 8.16
PARÁMETROS FLUJO "CRÍTICO"
Dc Tc Ac RHIDRÁULICO c Pc Jc F
(m) (m) (m
2
) (m) (m) (adim.) (adim.)
0.925 5.74 5.31 0.77 6.93 0.0116 1.00
Z1
Z2

27. Bibliografía básicaBibliografía básica
TEMA 5 FUENTES CON ESCORRENTÍA SUPERFICIALTEMA 5 FUENTES CON ESCORRENTÍA SUPERFICIAL
1. González, J. E. (2011): “Hidráulica de fuentes ornamentales e instalaciones
acuáticas”, ISBN: 978-84-614-7971-9. Depósito legal: 394- 2011. Lugar de
publicación: España. páginas 133 a 168.
2. González, J. E. (2010): “Selección de temas de Hidráulica”, 2da. Edición,
páginas 157- 195, Servicio de Publicaciones/ Universidad de La Laguna, S/ C
de Tenerife, I. Canarias, España.

28. PRÓXIMA ACTIVIDAD
En la próxima actividad se verán, dentro del tema 6 “Fuentes basadas en chorros
y láminas ”, los aspectos siguientes:
6.1 Generalidades.
6.2 Tipos y características técnicas de las boquillas.
6.3 Ejemplos prácticos.