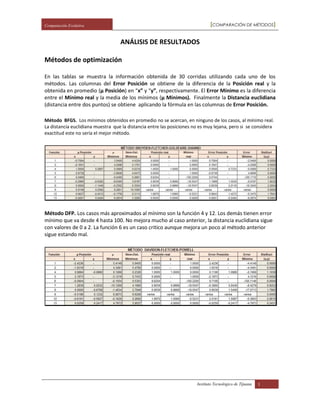
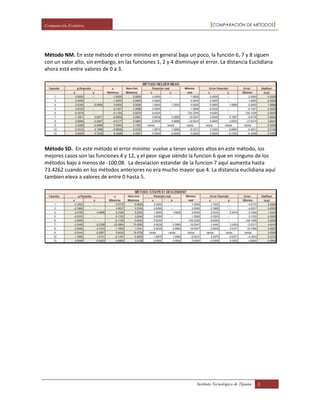
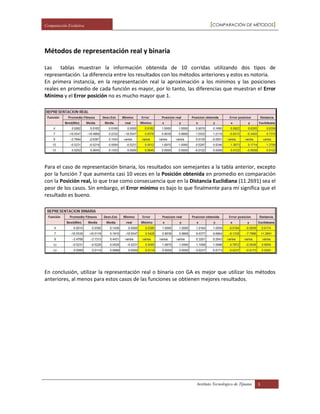
El documento analiza y compara los resultados de utilizar diferentes métodos de optimización (BFGS, DFP, NM y SD) y representaciones (real y binaria) para resolver funciones objetivo. Los métodos BFGS, DFP y SD no lograron aproximarse a los mínimos reales, mientras que el método NM tuvo un mejor desempeño. La representación real obtuvo mejores resultados que la binaria, con errores menores en la posición y aproximaciones más cercanas a los mínimos reales. En general, el documento concluye que utilizar algoritmos gen

1. ANÁLISIS DE RESULTADOS<br />Métodos de optimización<br />En las tablas se muestra la información obtenida de 30 corridas utilizando cada uno de los métodos. Las columnas del Error Posición se obtiene de la diferencia de la Posición real y la obtenida en promedio (µ Posición) en “x” y “y”, respectivamente. El Error Mínimo es la diferencia entre el Mínimo real y la media de los mínimos (µ Mínimos). Finalmente la Distancia euclidiana (distancia entre dos puntos) se obtiene aplicando la fórmula en las columnas de Error Posición.<br />Método BFGS. Los mínimos obtenidos en promedio no se acercan, en ninguno de los casos, al mínimo real. La distancia euclidiana muestra que la distancia entre las posiciones no es muy lejana, pero si se considera exactitud este no sería el mejor método.<br />Método DFP. Los casos más aproximados al mínimo son la función 4 y 12. Los demás tienen error mínimo que va desde 4 hasta 100. No mejora mucho al caso anterior, la distancia euclidiana sigue con valores de 0 a 2. La función 6 es un caso critico aunque mejora un poco al método anterior sigue estando mal.<br />Método NM. En este método el error mínimo en general baja un poco, la función 6, 7 y 8 siguen con un valor alto, sin embargo, en las funciones 1, 2 y 4 disminuye el error. La distancia Euclidiana ahora está entre valores de 0 a 3.<br />Método SD. En este método el error minimo vuelve a tener valores altos en este método, los mejores casos son las funciones 4 y 12, y el peor sigue siendo la funcion 6 que en ninguno de los métodos bajo a menos de -100.08. La desviacion estandar de la funcion 7 aquí aumenta hasta 73.4262 cuando en los métodos anteriores no era mucho mayor que 4. La distancia euclidiana aquí tambien eleva a valores de entre 0 hasta 5.<br />Métodos de representación real y binaria<br />Las tablas muestran la información obtenida de 10 corridas utilizando dos tipos de representación. La diferencia entre los resultados con los métodos anteriores y estos es notoria. <br />En primera instancia, en la representación real la aproximación a los mínimos y las posiciones reales en promedio de cada función es mayor, por lo tanto, las diferencias que muestran el Error Mínimo y el Error posición no es mucho mayor que 1.<br />Para el caso de representación binaria, los resultados son semejantes a la tabla anterior, excepto por la función 7 que aumenta casi 10 veces en la Posición obtenida en promedio en comparación con la Posición real, lo que trae como consecuencia que en la Distancia Euclidiana (11.2691) sea el peor de los casos. Sin embargo, el Error mínimo es bajo lo que finalmente para mí significa que el resultado es bueno. <br />En conclusión, utilizar la representación real o binaria con GA es mejor que utilizar los métodos anteriores, al menos para estos casos de las funciones se obtienen mejores resultados.<br />