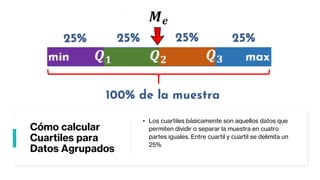
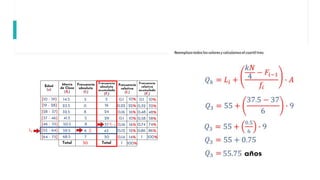
Este documento describe los cuartiles y cómo calcularlos. Explica que los cuartiles dividen una distribución de datos en cuatro partes iguales, con el primer cuartil (Q1) dejando el 25% de los datos por debajo y el tercer cuartil (Q3) dejando el 75% por debajo. Detalla la fórmula para calcular los cuartiles y aplica esta fórmula a un ejemplo numérico para ilustrar cómo encontrar Q3.

1. ESTADÍSTICA APLICADA
A LA EDUCACIÓN
CUARTILES
Carlos Massuh Villavicencio
Esta foto de Autor desconocido está bajo licencia CC BY-SA

2. La expresión resumida de la información
• El objetivo de describir el conjunto de datos se logrará indicando tres tipos
diferentes de medidas. En primer lugar, haremos referencia a las medidas de
posición. Estas medidas nos indicarán en torno a qué valores se distribuyen las
observaciones.
• Dentro de las medidas de posición, definiremos las medidas centrales, (también llamadas de
centralidad o de tendencia central), y no centrales o de orden.
• En segundo lugar, mencionaremos las medidas de dispersión (conocidas también como de
variabilidad), que mostrarán si los datos están concentrados alrededor de las medidas de
centralidad o si están dispersos, alejados de esas medidas centrales.
• En tercer lugar, nos detendremos en la forma que asume la distribución y allí, aunque hay
otras medidas, solo nos ocuparemos de describir la simetría o asimetría que manifiesta el
conjunto de datos.

3. Medidas de orden

4. Medidas no
centrales
• Si la variable tiene un nivel de medición
ordinal o superior, entonces podemos usar
el mismo razonamiento con el que
definimos la mediana para hacer cortes
más finos en una distribución de
frecuencia.
• Así, si la mediana nos indica el valor de la
variable que deja por debajo la mitad de los
casos, es lícito preguntar también por el
valor que deja por debajo un cuarto de los
casos, o también el que deja por debajo las
tres cuartas partes de las observaciones.

5. Medidas no
centrales
• Estos puntos de corte se denominan
respectivamente: primer cuartil y
tercer cuartil.
• El primer cuartil es el valor de la
variable que deja por debajo un
cuarto, o el 25% del total de
observaciones.
• El tercer cuartil es el valor que
deja por debajo las tres cuartas
partes o el 75% del total de
observaciones.

6. • El primer cuartil es el valor de la
variable que deja un cuarto (25%) de
los casos por debajo y tres cuartos
(75%) por encima. Se indica Q1.

7. • El tercer cuartil es el valor de la variable
que deja tres cuartos (75%) de los casos
por debajo y un cuarto (25%) por
encima. Se indica Q3.

8. Cómo calcular
Cuartiles para
Datos Agrupados
• Los cuartiles básicamente son aquellos datos que
permiten dividir o separar la muestra en cuatro
partes iguales. Entre cuartil y cuartil se delimita un
25%

9. • El segundo cuartil corresponde
al mismo valor de la mediana ya
que divide los datos en un 50%
a lado y lado.
• Para calcular cualquier cuartil
debemos identificar el intervalo de
trabajo. Para ello utilizamos la
siguiente expresión:

10. Vamos a calcular el Cuartil 3 (Q3)

11. • N es la cantidad de datos de la
muestra. En este caso N vale 50
porque estamos analizando las
edades de 50 personas.
• K corresponde al número del cuartil.
Si vamos a calcular el cuartil tres (Q3)
entonces K vale 3; s i vamos a
calcular el cuartil dos (Q2) entonces K
vale 2, y s i vamos a calcular el cuartil
uno (Q1) entonces K vale 1.

12. El cuartil debe estar ubicado en el dato número 37.5…
vamos a UBICAR en cuál intervalo tendríamos un
acumulado en el cuál cabrían 37.5 datos.
Revisemos la tabla de frecuencias:

13. • No sirve el intervalo [46 – 55) porque
el acumulado es 37… y necesitamos
que quepan hasta 37.5… por eso el
intervalo que nos SIRVE es el de [55 –
64) donde caben hasta 43
acumulados hasta él. Es fácil... en el
primer acumulado que quepa… ese es
el intervalo de trabajo.
• Ya tenemos el intervalo de trabajo,
ahora vamos a reemplazar los datos
en la fórmula de los cuartiles:

14. • N es la cantidad de datos de la muestra. En
este caso N vale 50
• K es el número del cuartil. En este caso K
vale 3
• Fi-1 es la frecuencia absoluta acumulada
ANTERIOR al intervalo de trabajo. En este
caso Fi-1 vale 37
• fi es la frecuencia absoluta del intervalo de
trabajo. En este caso fi vale 6
• Li es el límite inferior del intervalo de trabajo.
En este caso Li vale 55
• A es la amplitud del intervalo de trabajo. En
este caso A vale 9

16. • Analicemos el resultado: Para este
ejercicio tenemos que el sujeto de
menor edad tiene 10 años… y el de
mayor edad tiene 73 años. El
cuartil tres (Q3) vale 55.75 años…
eso significa que el 75% de la
muestra está entre 10 y 55.75
años… y el otro 25% de la muestra
tiene entre 55.75 y 73 años de
edad.

17. ¡Gracias!