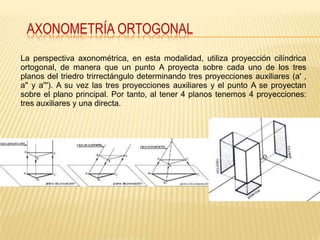
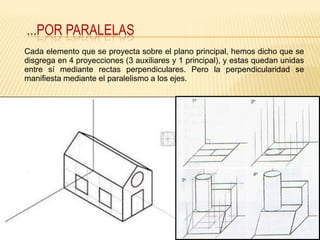
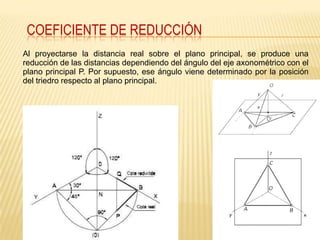
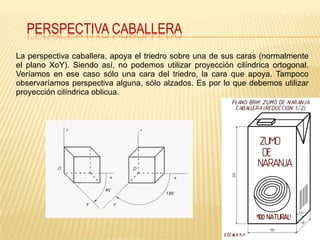
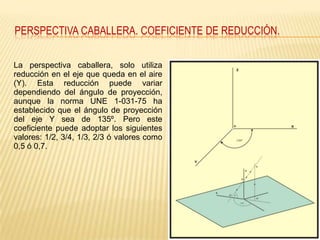
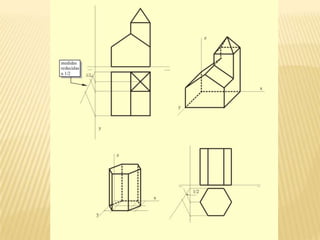
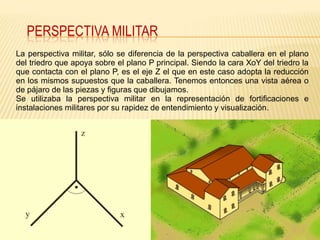
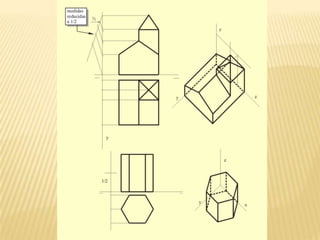
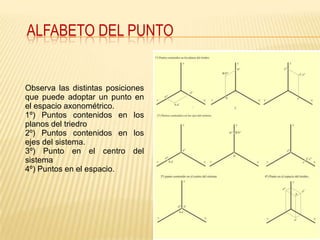
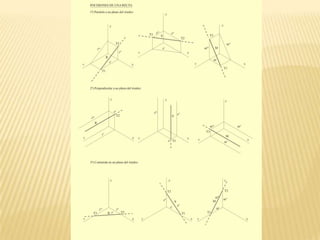
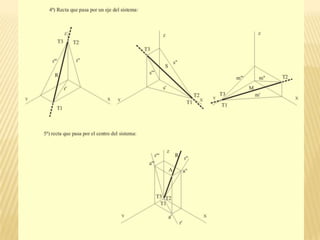
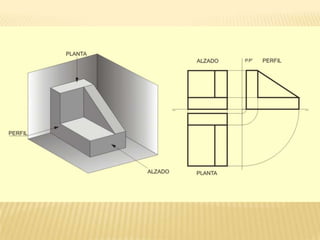
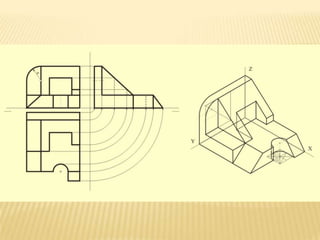
Este documento explica los principios básicos del sistema axonométrico de representación gráfica en 3D. Describe los cuatro planos de proyección utilizados (tres planos auxiliares y un plano principal), y cómo los objetos se proyectan en estos planos para crear una representación tridimensional. También cubre conceptos como la proyección cilíndrica ortogonal y oblicua, los coeficientes de reducción, y los diferentes tipos de axonométricas como isométrica, dimétrica y trimétrica.

1. EL SISTEMA AXONOMÉTRICO

2. QUÉ SABÍAS
La perspectiva axonométrica utiliza las tres direcciones
fundamentales del espacio, alto - ancho - profundo, para
desarrollar las distintas perspectivas que puede presentar este
sistema.

3. LA PROYECCIÓN DE LOS EJES
El triedro - trirrectángulo determina los tres ejes del sistema axonométrico (X, Y
y Z). El vértice del triedro es el centro del sistema. Los objetos se colocarán
sobre el triedro trirrectángulo y se proyectará todo sobre el plano principal.

4. AXONOMETRÍA ORTOGONAL
La perspectiva axonométrica, en esta modalidad, utiliza proyección cilíndrica
ortogonal, de manera que un punto A proyecta sobre cada uno de los tres
planos del triedro trirrectángulo determinando tres proyecciones auxiliares (a' ,
a'' y a'''). A su vez las tres proyecciones auxiliares y el punto A se proyectan
sobre el plano principal. Por tanto, al tener 4 planos tenemos 4 proyecciones:
tres auxiliares y una directa.

5. PRINCIPIOS BÁSICOS
En el sistema axonométrico intervienen 4 planos de proyección:
 3 planos auxiliares que forman un triedro - trirrectángulo, es decir, que
determinan tres ángulos rectos entre sí
 1 plano principal en el que se apoya el triedro. El triedro Puede adoptar
múltiples posiciones con respecto al plano principal:
 En las axonometrías ortogonales se apoyará el triedro sobre su vértice,
pudiendo adoptar cualquier
inclinación respecto al plano
principal.
 En las axonometrías oblicuas,
apoyará el triedro una de sus
caras sobre el plano principal
para obtener la perspectiva.

6. ...POR PARALELAS
Cada elemento que se proyecta sobre el plano principal, hemos dicho que se
disgrega en 4 proyecciones (3 auxiliares y 1 principal), y estas quedan unidas
entre sí mediante rectas perpendiculares. Pero la perpendicularidad se
manifiesta mediante el paralelismo a los ejes.

7. COEFICIENTE DE REDUCCIÓN
Al proyectarse la distancia real sobre el plano principal, se produce una
reducción de las distancias dependiendo del ángulo del eje axonométrico con el
plano principal P. Por supuesto, ese ángulo viene determinado por la posición
del triedro respecto al plano principal.

8. ISOMÉTRICO, DIMÉTRICO Y TRIMÉTRICO
Podemos deducir cómo se comporta el triedro cuando los ejes no adoptan
igual ángulo con respecto al plano principal. En esos casos, el coeficiente
de reducción varía para cada valor angular de cada eje.
 Por eso, en axonométrico isométrico (iso: igual - métrico: medida) los
tres ejes poseen igual coeficiente de reducción.
 En axonométrico dimétrico (dos medidas), dos ejes poseen igual
ángulo y uno varía su valor angular, por lo tanto, dos coeficientes.
 En axonométrico trimétrico (tres medidas), son tres los ejes que
desarrollan distinto coeficiente de reducción.

9. PERSPECTIVA CABALLERA
La perspectiva caballera, apoya el triedro sobre una de sus caras (normalmente
el plano XoY). Siendo así, no podemos utilizar proyección cilíndrica ortogonal.
Veríamos en ese caso sólo una cara del triedro, la cara que apoya. Tampoco
observaríamos perspectiva alguna, sólo alzados. Es por lo que debemos utilizar
proyección cilíndrica oblicua.

10. PERSPECTIVA CABALLERA. COEFICIENTE DE REDUCCIÓN.
La perspectiva caballera, solo utiliza
reducción en el eje que queda en el aire
(Y). Esta reducción puede variar
dependiendo del ángulo de proyección,
aunque la norma UNE 1-031-75 ha
establecido que el ángulo de proyección
del eje Y sea de 135º. Pero este
coeficiente puede adoptar los siguientes
valores: 1/2, 3/4, 1/3, 2/3 ó valores como
0,5 ó 0,7.

12. PERSPECTIVA MILITAR
La perspectiva militar, sólo se diferencia de la perspectiva caballera en el plano
del triedro que apoya sobre el plano P principal. Siendo la cara XoY del triedro la
que contacta con el plano P, es el eje Z el que en este caso adopta la reducción
en los mismos supuestos que la caballera. Tenemos entonces una vista aérea o
de pájaro de las piezas y figuras que dibujamos.
Se utilizaba la perspectiva militar en la representación de fortificaciones e
instalaciones militares por su rapidez de entendimiento y visualización.

14. ALFABETO DEL PUNTO
Observa las distintas posiciones
que puede adoptar un punto en
el espacio axonométrico.
1º) Puntos contenidos en los
planos del triedro
2º) Puntos contenidos en los
ejes del sistema.
3º) Punto en el centro del
sistema
4º) Puntos en el espacio.

15. ALFABETO DE LA RECTA
Uniendo dos puntos del espacio obtendremos una recta R que tendrá a su vez
cuatro proyecciones, una por cada plano. Siendo la proyección directa la que
surge al unir las proyecciones directas de dos puntos, y las demás proyecciones
de la recta con las proyecciones homólogas de los puntos (R, r', r'', r'''). También,
al igual que ocurría en sistema diédrico, las rectas poseen trazas con los planos
de proyección, es decir, los puntos donde interseccionan la recta con los planos
(T1, T2, T3).

18. ALFABETO DEL PLANO
El plano, al igual que en el sistema diédrico,
se representa mediante sus trazas (P', P'',
P'''). Observa las distintas posiciones que
puede adoptar un plano.

19. REPRESENTACIÓN DE CUERPOS SENCILLOS.
Para la representación de sólidos, es necesaria la
información que nos proporcionan sobre el sistema
diédrico, es decir, sobre la planta, alzado y perfil de la
pieza a representar. Debemos aprender a realizar el
paso de estos elementos de diédrico a axonométrico.

22. APRENDE CON ARTISTAS
Para aprender y disfrutar de las perspectivas y
sobre todo de mundos imposibles, quién mejor
que Escher. Maurits Cornelis Escher (1898-
1972) ha sido uno de los genios de la
interpretación de la geometría sobre el papel.
Sus perspectivas imposibles han hecho soñar e
imaginar a muchos otros mundos y otras
visiones de la realidad.
http://www.mcescher.com/