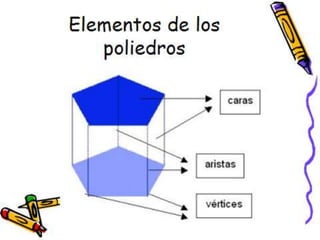
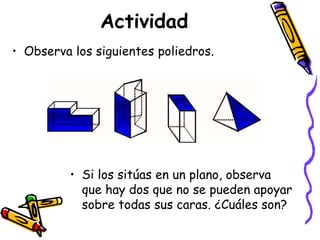
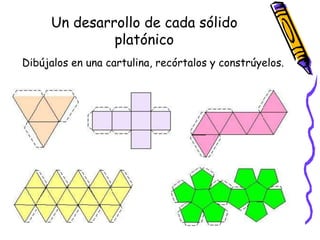
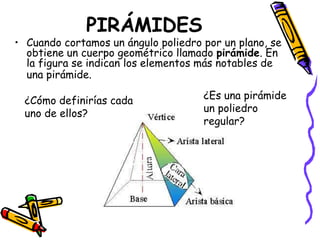
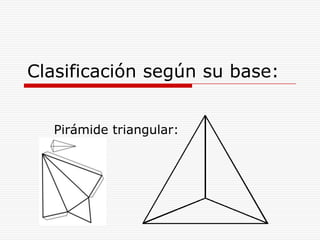
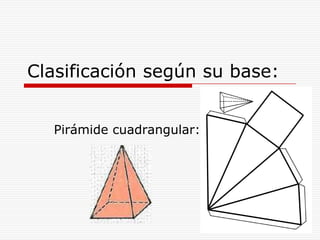
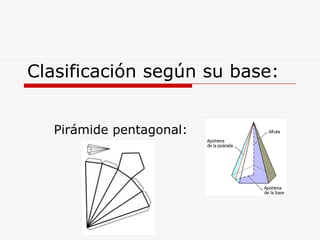
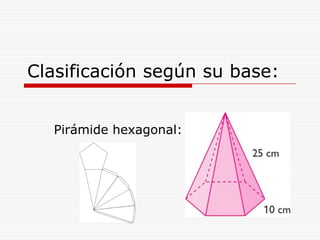
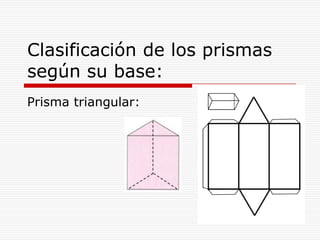
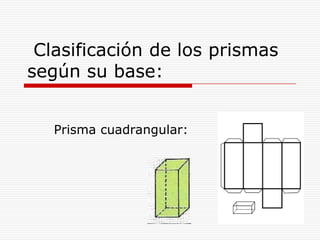
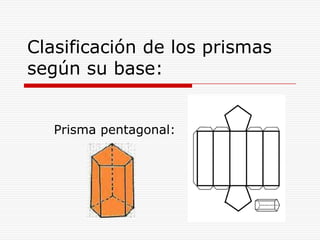
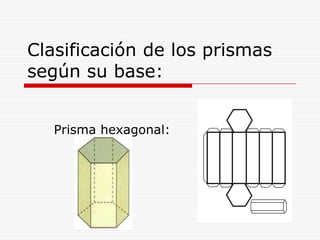
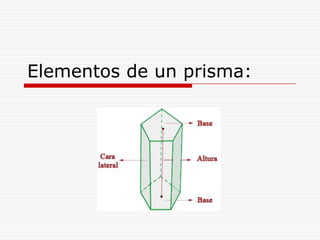
Este documento describe los diferentes tipos de cuerpos sólidos geométricos, incluyendo poliedros, pirámides, prismas y cuerpos redondos como conos, cilindros y esferas. Define cada forma geométrica y proporciona ejemplos de sus elementos. También incluye ejemplos de cómo estas formas aparecen en el entorno natural y construido.

1. CUERPOS SÓLIDOSUn cuerpo sólido es todo lo que ocupa lugar en el espacio.Los cuerpos geométricos pueden ser de dos clases: o formados por caras planas (poliedros), o teniendo alguna o todas sus caras curvas (cuerpos redondos).

2. DEFINICIÓNEstos cuerpos se llaman poliedros y podemos decir de forma simplificada que son sólidos limitados por caras en forma de polígonos.

4. DEFINICIÓNA los poliedros que tienen alguna cara sobre la que no se pueden apoyar, se les llama cóncavosy a los demás convexos. Nosotros vamos a trabajar siempre, salvo que se indique lo contrario, con poliedros convexos.

5. Actividad Observa los siguientes poliedros. Si los sitúas en un plano, observa que hay dos que no se pueden apoyar sobre todas sus caras. ¿Cuáles son?DEFINICIÓNUn poliedro es regular si todas sus caras son regulares e iguales.

6. TETRAEDRO REGULARFormado por tres triángulos equiláteros. Es el que tiene menor volumen de los cinco en comparación con su superficie. Representa el fuego. Está formado por 4 caras, 6 aristas y 4 vértices.FUEGO

7. OCTAEDRO REGULARFormado por ocho triángulos equiláteros. Gira libremente cuando se sujeta por vértices opuestos. Por ello, representa al aire en movimiento. Está formado por 8 caras, 12 aristas y 6 vértices.AIRE

8. ICOSAEDRO REGULARFormado por veinte triángulos equiláteros. Es el tiene mayor volumen en relación con su superficie y representa al agua. Tiene 20 caras, 30 aristas y 12 vértices.AGUA

9. HEXAEDRO REGULAR O CUBOFormado por seis cuadrados. Permanece estable sobre su base. Por eso representa la tierra. Está formado por 6 caras, 12 aristas y 8 vértices.TIERRA

10. DODECAEDRO REGULARFormado por doce pentágonos regulares. Corresponde al Universo, pues sus doce caras pueden albergar los doce signos del Zodiaco. Tiene 12 caras, 30 aristas y 20 vértices.EL UNIVERSO

11. DESARROLLO DE POLIEDROSSi en un poliedro cortamos por un número suficiente de aristas de forma que quede una sola pieza y la extendemos en el plano, obtenemos un desarrollo del poliedro.

12. Un desarrollo de cada sólido platónicoDibújalos en una cartulina, recórtalos y constrúyelos.

13. PIRÁMIDESCuando cortamos un ángulo poliedro por un plano, se obtiene un cuerpo geométrico llamado pirámide. En la figura se indican los elementos más notables de una pirámide.¿Es una pirámide un poliedro regular?¿Cómo definirías cada uno de ellos?

14. PIRÁMIDES Concepto:Es un cuerpo geométrico cuya base es un poígono cualquiera y cuyas caras laterales son triángulos que tienen un vértce común. Este vértice xomún se llama vértice o cúspide la pirámide.

15. Clasificación según su base:Pirámide triangular:

16. Clasificación según su base:Pirámide cuadrangular:

17. Clasificación según su base:Pirámide pentagonal:

18. Clasificación según su base:Pirámide hexagonal:

19. Elementos de una pirámide:- La base, que es un polígono cualquiera.- Las caras laterales, que son siempre triángulos.- Las aristas básicas, que son los lados del polígonos de la base.- Las aristas laterales, que son los lados delas caras laterales que sno son aristas básicas.- Los vértices de la base, que son los vértices del polígono de la base.- El vértice o cúspide, que es el punto en que se encuentran las aristas laterales.

20. Pirámides en el entorno:

21. Pirámides en el entorno:

22. TRONCO DE PIRÁMIDESi cortamos una pirámide por un plano, obtenemos un tronco de pirámide, que será recto u oblicuo, según que el plano sea o no paralelo a la base. Fíjate en que las caras laterales de un tronco de pirámide son trapecios y cuando éste es regular, entonces los trapecios son isósceles iguales y su altura coincide con la apotema del tronco de pirámide. Por otra parte, las bases son polígonos semejantes.FUENTE: http://www.juntadeandalucia.es/averroes/iesarroyo/matematicas/materiales/4eso/geometria/poliedros/poliedros.htm

23. PRISMA Concepto:Los prismas son poliedros que tienen dos caras paralelas que se llaman bases y el resto de caras son paralelogramos. Si estas caras son perpendiculares a las bases el prisma es recto, sino oblicuo.

24. Clasificación de los prismas según su base:Prisma triangular:

25. Clasificación de los prismas según su base:Prisma cuadrangular:

26. Clasificación de los prismas según su base:Prisma pentagonal:

27. Prisma hexagonal:Clasificación de los prismas según su base:

28. Elementos de un prisma:

29. Prismas en el entorno:

30. Prismas en el entorno:

31. Prismas en el entorno:

32. Concepto de cuerpos redondos:Los cuerpos redondos son el cono, cilindro y la esfera; se llaman tambien cuerpos de revolucion porque pueden obtenerse a partir de un rectángulo, de un triángulo rectángulo y de un semicírculo, respectivamente, haciendoles girar sobre su eje.

33. Concepto de cono:Es el cuerpo de revolución obtenido al hacer girar un triángulo rectángulo alrededor de uno de sus catetos.

34. Conos en el entorno:

35. Conos en el entorno:

36. Concepto de cilindro:El cilindro es un cuerpo de revolución generado por un rectángulo que gira alrededor de uno de sus lados.

37. Cilindros en el entorno:

38. Concepto de esfera:La esfera es un cuerpo de revolución generado por una circunferencia que gira alrededor de cualquiera de sus diámetros.

39. HemisferioEs cada una de las partes en que queda dividida la superficie esférica por un plano que pasa por el centro de la esfera, llamado plano diametral.

40. SemiesferaParte de una esfera comprendida entre dos planos que se cortan en el diámetro de aquella.

41. Esfera en el entorno:

42. Esfera en el entorno:

43. Esfera en el entorno:

44. ………………...Fín……………….