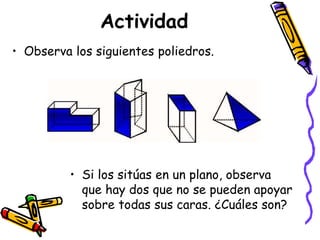
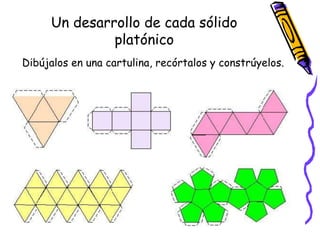
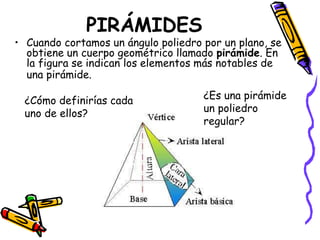
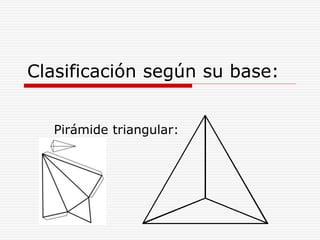
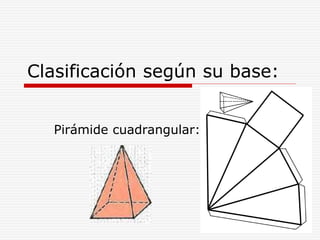
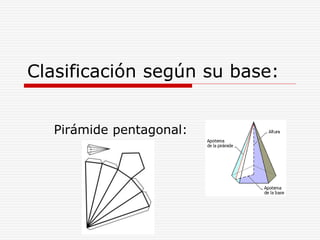
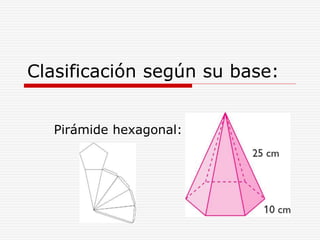
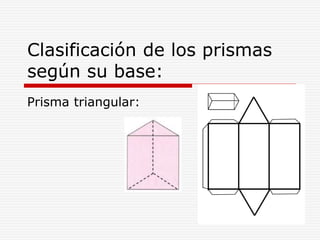
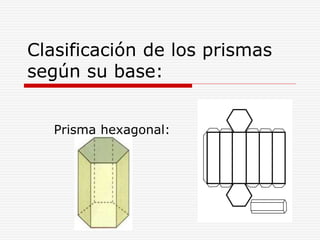
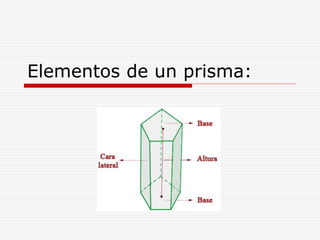
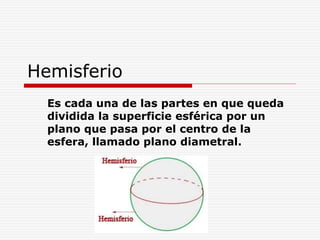
Este documento define y describe varios tipos de cuerpos sólidos, incluyendo poliedros, pirámides, prismas y cuerpos redondos. Explica que los poliedros están formados por caras planas, mientras que los cuerpos redondos como conos, cilindros y esferas se forman girando figuras alrededor de un eje. También proporciona ejemplos de cada forma geométrica y cómo se ven en el mundo real.

1. CUERPOS SÓLIDOS
• Un cuerpo sólido es todo lo que ocupa
lugar en el espacio.
• Los cuerpos geométricos pueden ser
de dos clases: o formados por caras
planas (poliedros), o teniendo alguna o
todas sus caras curvas (cuerpos
redondos).

2. DEFINICIÓN
• Estos cuerpos se llaman poliedros y
podemos decir de forma
simplificada que son sólidos
limitados por caras en forma de
polígonos.

4. DEFINICIÓN
• A los poliedros que tienen alguna cara
sobre la que no se pueden apoyar, se
les llama cóncavos y a los demás
convexos. Nosotros vamos a trabajar
siempre, salvo que se indique lo
contrario, con poliedros convexos.

5. Actividad
• Observa los siguientes poliedros.
• Si los sitúas en un plano, observa
que hay dos que no se pueden apoyar
sobre todas sus caras. ¿Cuáles son?

6. DEFINICIÓN
• Un poliedro es regular si todas sus
caras son regulares e iguales.

7. TETRAEDRO REGULAR
• Formado por tres triángulos equiláteros. Es el que
tiene menor volumen de los cinco en comparación
con su superficie. Representa el fuego. Está
formado por 4 caras, 6 aristas y 4 vértices.
FUEGO

8. OCTAEDRO REGULAR
• Formado por ocho triángulos equiláteros. Gira
libremente cuando se sujeta por vértices opuestos.
Por ello, representa al aire en movimiento. Está
formado por 8 caras, 12 aristas y 6 vértices.
AIRE

9. ICOSAEDRO REGULAR
• Formado por veinte triángulos equiláteros. Es el
tiene mayor volumen en relación con su superficie y
representa al agua. Tiene 20 caras, 30 aristas y 12
vértices.
AGUA

10. HEXAEDRO REGULAR O
CUBO
• Formado por seis cuadrados. Permanece estable
sobre su base. Por eso representa la tierra. Está
formado por 6 caras, 12 aristas y 8 vértices.
TIERRA

11. DODECAEDRO REGULAR
• Formado por doce pentágonos regulares.
Corresponde al Universo, pues sus doce caras
pueden albergar los doce signos del Zodiaco. Tiene
12 caras, 30 aristas y 20 vértices.
EL UNIVERSO

12. DESARROLLO DE
POLIEDROS
• Si en un poliedro cortamos por un
número suficiente de aristas de
forma que quede una sola pieza y la
extendemos en el plano, obtenemos
un desarrollo del poliedro.

13. Un desarrollo de cada sólido
platónico
Dibújalos en una cartulina, recórtalos y constrúyelos.

14. PIRÁMIDES
• Cuando cortamos un ángulo poliedro por un plano, se
obtiene un cuerpo geométrico llamado pirámide. En
la figura se indican los elementos más notables de
una pirámide.
¿Cómo definirías cada
uno de ellos?
¿Es una pirámide
un poliedro
regular?

15. PIRÁMIDES Concepto:
Es un cuerpo geométrico cuya base es un
poígono cualquiera y cuyas caras laterales son
triángulos que tienen un vértce común. Este
vértice xomún se llama vértice o cúspide la
pirámide.

16. Clasificación según su base:
Pirámide triangular:

17. Clasificación según su base:
Pirámide cuadrangular:

18. Clasificación según su base:
Pirámide pentagonal:

19. Clasificación según su base:
Pirámide hexagonal:

20. Elementos de una pirámide:
- La base, que es un polígono cualquiera.
- Las caras laterales, que son siempre triángulos.
- Las aristas básicas, que son los lados del polígonos de
la base.
- Las aristas laterales, que son los lados delas caras
laterales que sno son aristas básicas.
- Los vértices de la base, que son los vértices del
polígono de la base.
- El vértice o cúspide, que es el punto en que se
encuentran las aristas laterales.

21. Pirámides en el entorno:

22. Pirámides en el entorno:

23. TRONCO DE PIRÁMIDE
• Si cortamos una pirámide por un plano,
obtenemos un tronco de pirámide, que será
recto u oblicuo, según que el plano sea o no
paralelo a la base. Fíjate en que las caras
laterales de un tronco de pirámide son
trapecios y cuando éste es regular, entonces
los trapecios son isósceles iguales y su altura
coincide con la apotema del tronco de
pirámide. Por otra parte, las bases son
polígonos semejantes.
FUENTE: http://www.juntadeandalucia.es/averroes/iesarroyo/matematicas/materiales/4eso/geometria/poliedros/poliedros.htm

24. PRISMA Concepto:
Los prismas son poliedros que tienen dos
caras paralelas que se llaman bases y el
resto de caras son paralelogramos. Si
estas caras son perpendiculares a las
bases el prisma es recto, sino oblicuo.

25. Clasificación de los prismas
según su base:
Prisma triangular:

26. Clasificación de los prismas
según su base:
Prisma cuadrangular:

27. Clasificación de los prismas
según su base:
Prisma pentagonal:

28. Prisma hexagonal:
Clasificación de los prismas
según su base:

29. Elementos de un prisma:

30. Prismas en el entorno:

31. Prismas en el entorno:

32. Prismas en el entorno:

33. Concepto de cuerpos
redondos:
Los cuerpos redondos son el cono, cilindro y
la esfera; se llaman tambien cuerpos de
revolucion porque pueden obtenerse
a partir de un rectángulo, de un triángulo
rectángulo y de un semicírculo,
respectivamente, haciendoles girar sobre su
eje.

34. Concepto de cono:
Es el cuerpo de revolución obtenido al
hacer girar un triángulo rectángulo
alrededor de uno de sus catetos.

35. Conos en el entorno:

36. Conos en el entorno:

37. Concepto de cilindro:
El cilindro es un cuerpo de revolución
generado por un rectángulo que gira
alrededor de uno de sus lados.

38. Cilindros en el entorno:

39. Concepto de esfera:
La esfera es un cuerpo de revolución
generado por una circunferencia que
gira alrededor de cualquiera de sus
diámetros.

40. Hemisferio
Es cada una de las partes en que queda
dividida la superficie esférica por un
plano que pasa por el centro de la
esfera, llamado plano diametral.

41. Semiesfera
Parte de una esfera comprendida
entre dos planos que se cortan en
el diámetro de aquella.

42. Esfera en el entorno:

43. Esfera en el entorno:

44. Esfera en el entorno:

45. ………………...Fín……………….