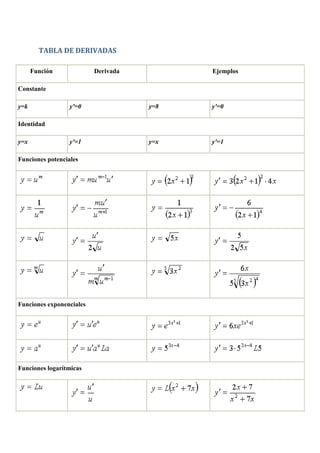
[1] Este documento presenta información sobre derivadas y problemas de derivadas. Incluye una tabla de derivadas comunes, reglas para derivar sumas, productos y funciones compuestas, y una colección de 20 ejercicios de derivadas resueltos. [2] También incluye un boletín de trabajo con 4 problemas de derivadas para que el estudiante resuelva. El documento proporciona información fundamental sobre el cálculo de derivadas a través de ejemplos y ejercicios resueltos.

1. Analysis
Derivadas. Problemas
OpenUepc.com 1.1.4.6.1 Ver 01:03/02/2010

3. NOTA
La clasificación decimal de todos los temas de este manual tienen
implícito el comienzo 1.1.4.6.1 correspondiente a
1 SCIENCE
1.1 MATHEMATICS
1.1.4 ANALYSIS
1.1.4.6 .1 DIFERENCIACION
COPYLEFT
Este material así como los applets, powerpoints, videos y archivos de
sonido asociados, puede ser distribuido bajo los términos y condiciones
definidos en Open Publication License versión 1.0 o posterior (La
versión más reciente está disponible en
http://www.opencontent.org/openpub/).
El contenido está sujeto a constantes cambios sin previo aviso. Su fin
es didáctico y solo pretende la universalización de la cultura. Está
escrito en base a la colaboración de las miles de personas que
componen nuestra comunidad OpenUepc. Se ha exigido a los autores
que referencien todas las fuentes utilizadas y figuran al final del texto.
Cualquier distribución del mismo debe mencionar a OpenUepc como
fuente.
Miguel Pérez Fontenla
miguelperez@edu.xunta.es
INDICE AUTORES
Iniciado por: Miguel Pérez Fontenla
22/01/2010

5. TABLA DE DERIVADAS
Función Derivada Ejemplos
Constante
y=k y'=0 y=8 y'=0
Identidad
y=x y'=1 y=x y'=1
Funciones potenciales
Funciones exponenciales
Funciones logarítmicas

6. Funciones trigonométricas
Derivadas de sumas, restas, productos y cocientes de funciones

7. Regla de la cadena
( g o f ) ( x) = { g [ f ( x)]} ' = g '[ f ( x)] ⋅ f '( x)
'

8. +
COLECCIÓN DE 20 EJERCICIOS
Presento a continuación una colección de 20 derivadas resueltas que de saberlas hacer todas,
es presumible que estas perfectamente preparado en lo que respecta al cálculo de derivadas.
1.- Calcular la derivada de la función f(x)= x – cos x
π
2.- Calcular la derivada de la función f ( x ) = x 4 − sin x − ln x en x=
2
+
3.- Calcular la derivada de la función f ( x) = x ln x x∈
2
4.- Calcular la derivada de la función f ( x) = x sin x
x sin x − 1
5.- Calcular la derivada de la función f ( x ) =
x3
x tan x − cos x
6.- Calcular la derivada de la función f ( x ) =
ln x
2
7.- Calcular la derivada de la función f ( x) = cos x
8.- Calcular la derivada de la función f ( x) = ln cos x
9.- Calcular la derivada de la función f ( x) = e x sin x
10.- Calcular la derivada de la función f ( x) = ln(ln x)
11.- Calcular la derivada de la función f ( x) = sen 2 ( x 2 )
12.- Calcular la derivada de la función f ( x ) = x 3 + lg 2 x 2
2
x −1 
13.- Calcular la derivada de la función f ( x ) = 3 
 
 x 
x
14.- Calcular la derivada de la función f ( x ) = arctan
x +1
ln x
15.- Calcular la derivada de la función f ( x ) = arc sec
x
16.- Calcular la derivada de la función f ( x) = x x
17.- Calcular la derivada de la función f ( x) = xl n x
18.- Calcular la derivada de la función f ( x) = x tan x
1 1− x
19.- Calcular la derivada de la función f ( x) = ln
2 1+ x
20.- Calcular la derivada de la función f ( x) = ln x + x 2 + 1
Ejercicios Propuestos
Calcular la derivada de la función f ( x) = ln x + x 2 − 1
1 1+ x
Calcular la derivada de la función f ( x) = ln
2 1− x
| COLECCIÓN DE 20 EJERCICIOS 1

9. +
Soluciones
1.- Calcular la derivada de la función f(x)= x – cos x
f '( x) = ( x − cos x ) ' = x '− cos' x = 1 − (− sin x) = 1 + sin x
π
2.- Calcular la derivada de la función f ( x ) = x 4 − sin x − ln x en x=
2
3
1 π  π  π 1 π3 2 π4 −4
f '( x) = ( x 4 − sin x − ln x ) = 4 x 3 − cos x − ; f '   = 4   − cos − =
'
− =
x 2 2 2 π 2 π 2π
2
+
3.- Calcular la derivada de la función f ( x ) = x ln x x ∈
Al estar definido x>0 ya no tenemos problemas con la definición de la función, pues sólo
tendríamos problemas si apareciesen neperianos de números negativos
1
f '( x) = ( x ln x ) ' = x 'ln x + x ( ln x ) ' = 1⋅ ln x + x   = ln x + 1
 x
4.- Calcular la derivada de la función f ( x) = x 2 sin x
f '( x ) = ( x 2 sin x ) ' = ( x 2 ) 'sin x + x 2 ( sin x ) ' = 2 x ⋅ sin x + x 2 cos x
x sin x − 1
5.- Calcular la derivada de la función f ( x ) =
x3
 x 'sin x + x ( sin x ) '− 0  x − ( x sin x − 1) x
 3 ( sin x + x cos x ) x 3 − x 4 sin x + x3
' 3
 x sin x − 1  
f '( x ) =   = = = ...
 x3  x6 x6
sin x + x cos x − x sin x + 1
... =
x3
x tan x − cos x
6.- Calcular la derivada de la función f ( x ) =
ln x
 x tan x − cos x 
'
 x ' tan x + x ( tan x ) '− ( cos x ) ' ln x − ( x tan x − cos x )( ln x ) '
 
f '( x ) =   = = ...
 ln x  ln 2 x
1
( tan x + x tan 2
x + sin x ) ln x − ( x tan x − cos x )
x
... =
ln 2 x
7.- Calcular la derivada de la función f ( x) = cos x 2
f '( x) = ( cos x 2 ) = − sin x 2 ( 2 x ) = −2 x sin x 2
'
8.- Calcular la derivada de la función f ( x) = ln cos x
1
f '( x ) = ( ln cos x ) =
'
( − sin x ) = − tan x
cos x
| COLECCIÓN DE 20 EJERCICIOS 2

10. +
9.- Calcular la derivada de la función f ( x) = e x sin x
f '( x) = ( 3x cos x ) = 3x cos x ln 3 ( x cos x ) ' = 3x cos x ln 3 ( cos x − x sin x )
'
10.- Calcular la derivada de la función f ( x) = ln(ln x)
1 1 1
f '( x ) = ( ln(ln x ) ) =
'
⋅ =
ln x x x ln x
11.- Calcular la derivada de la función f ( x) = sen 2 ( x 2 )
f '( x) = ( sin 2 ( x 2 ) ) = 2 ( sin x 2 )( cos x 2 ) ( 2 x )
'
12.- Calcular la derivada de la función f ( x ) = x 3 + lg 2 x 2
( )
1  2 1
'

f '( x ) = x 3 + lg 2 x 2 = 3 x + 2 lg 2 e ⋅ 2 x 
2 
2 x + lg 2 x 
3 x 
2
x −1 
13.- Calcular la derivada de la función f ( x ) = 
  3
 x 
' 2 −1
  x − 1 2  2  x − 1  3 −1 x − ( x − 1) 2  x − 1  3 1 2 x
f '( x ) =  3    =   2
=   2
= 2 3
  3 x  3 x  x 3x x −1
 
x  x

x
14.- Calcular la derivada de la función f ( x ) = arctan
x +1
( x + 1)  1 
2
 x 
'
1  ( x + 1) − x  1
f '( x ) =  arctan  =
 =  =
 ( x + 1)2  x 2 + ( x + 1) 2  x + 1 2  2x + x +1
 x + 1   x 2   ( ) 
2
  +1  
 x +1
ln x
15.- Calcular la derivada de la función f ( x ) = arc sec
x
'
 ln x  1 − ln x
ln x 
'  
  x  x2
f '( x) =  arc sec  = =
 x  ln x  ln x  2 ln x  ln x 
2
  −1   −1
x  x  x  x 
16.- Calcular la derivada de la función f ( x) = x x
Este tipo de derivadas en las que aparecen variables en la base y en el exponente se resuelven
tomando previamente logaritmos neperianos en la expresión a derivar, para posteriormente
aplicar la Regla de la Cadena de la siguiente forma
1 1
f ( x ) = x x ⇔ ln f ( x ) = x ln x ⇒ ( ln f ( x ) ) ' = ( x ln x ) ' ⇒ f '( x ) = 1ln x + x ⇒ f '( x ) = x x ( ln x + 1)
f ( x) x
17.- Calcular la derivada de la función f ( x) = xl n x
| COLECCIÓN DE 20 EJERCICIOS 3

11. +
1 2 ln x  2 ln x 
f ( x) = x ln x ⇔ ln f ( x) = ln x ⋅ ln x = ln 2 x ⇒ f '( x) = ⇒ f '( x) = x ln x  
f ( x) x  x 
18.- Calcular la derivada de la función f ( x) = x tan x
1 1 1  ln x tan x 
f ( x) = x tan x ⇔ ln f ( x) = tan x ln x ⇒ f '( x) = 2
ln x + tan x ⇒ f '( x) = x tan x  2
+ 
f ( x) cos x x  cos x x 
1 1− x
19.- Calcular la derivada de la función f ( x) = ln
2 1+ x
1 1 −1(1 + x ) − (1 − x ) 1 1 + x − 2 − x + x 1 1
f '( x) = = = =
2 1− x (1 + x )
2
2 1 − x (1 + x ) 2 (1 − x )(1 + x ) 1 − x 2
1+ x
20.- Calcular la derivada de la función f ( x ) = ln x + x 2 + 1
1 2x 1 x2 + 1 + x 1
f '( x) = 1+ = =
x + x2 + 1 2 x2 + 1 x + x2 + 1 x2 + 1 x2 + 1
Ejercicios Propuestos
Calcular la derivada de la función f ( x ) = ln x + x 2 − 1
1 1+ x
Calcular la derivada de la función f ( x) = ln
2 1− x
| COLECCIÓN DE 20 EJERCICIOS 4

12. +
BOLETÍN DE TRABAJO nº 1
Calcula las derivadas de las siguientes funciones
1. f ( x )= 3 x 5 − 2 x 4 + 5 x 3 − 3 x − 1
2. f ( x )= ( −2 x 3 )( 4 x 2 )
3x 2
3. f ( x)= 3
2x
4. f ( x )= (−2 x 3 )( 2 x )
x +1
5. f ( x )=
x −1
lg x
6. f ( x)= 2
ln x
cos x
7. f ( x )=
senx
3x
8. f ( x)= 3
x
1
9. f ( x )= 3
x
1
10. f ( x )=
ln x
| BOLETÍN DE TRABAJO nº 1 5

13. +
BOLETÍN DE TRABAJO nº 2
Calcula las derivadas de las siguientes funciones
1. f ( x )= x
2. f ( x )= x −2
x −2
3. f ( x)=
x3
4. f ( x )= 2 x 3 − 3 x −2
1
5. f ( x )= − 2
x
1
6. f ( x )=
senx + cos x
senx − cos x
7. f ( x )=
senx + cos x
1 − ln x
8. f ( x )=
1 + ln x
1− x2
9. f ( x)=
1 − x −2
x − 2x
10. f ( x)=
1+ 2x
| BOLETÍN DE TRABAJO nº 2 6

14. +
BOLETÍN DE TRABAJO nº 3
Calcula las derivadas de las siguientes funciones
e −1
1. f ( x )=
ln e
2. f ( x)= xe x − x ln x
3. f ( x)= e x ⋅ ln x
ex
4. f ( x)=
ln x
1− ex
5. f ( x)=
1 + ln x
6. f ( x)= (1 − ln x)( x + e x )
7. f ( x)= x e
8. f ( x)= x e ⋅ e x
1+ ex
9. f ( x)=
1− ex
ln x − e x
10. f ( x)=
ln x + e x
| BOLETÍN DE TRABAJO nº 3 7

15. +
BOLETÍN DE TRABAJO nº 4
Calcula las derivadas de las siguientes funciones
1. f ( x)= x 3 ⋅ 3 x
3x
2. f ( x)=
lg 3 x
3 x + lg 3 x
3. f ( x)=
3 x − lg 3 x
4. f ( x)= senx ⋅ tgx
senx
5. f ( x)=
tgx
x − senx
6. f ( x )=
x + cos x
cos x − senx
7. f ( x)=
tgx + cos x
cos x ⋅ senx
8. f ( x)=
tgx ⋅ cos x
cos x − 1
9. f ( x)=
tgx + x
x − senx
10. f ( x )=
x + cos x
| BOLETÍN DE TRABAJO nº 4 8

16. +
BOLETÍN DE TRABAJO nº 5
Calcula las derivadas de las siguientes funciones
1. f ( x)= x 3 − 3 x − 3 x
2. f ( x)= ( x )(3 )
3 x
lg 3 x
3. f ( x)=
3x
ln x
4. f ( x )= 3
3
x3 − 3x
5. f ( x)=
(lg 3 x )3 x
1 − x3
6. f ( x)=
1 + 3x
1 − ln x
7. f ( x)=
1 + lg 3 x
8. f ( x )= x 3 − 3 x( )(
3
x )
x + ln x
9. f ( x )= 3
x − lg 3 x
10. f ( x)= 3 3 x
| BOLETÍN DE TRABAJO nº 5 9

17. +
BOLETÍN DE TRABAJO nº 6
Calcula las derivadas de las siguientes funciones
1. f ( x)= 3 x 5
2. f ( x)= x 15 − x
1
3. f ( x )= 2
x
x3
4. f ( x)= 5
x
x −1
5. f ( x )= 5
x
6. f ( x)= 5 x 4
7. f ( x)= 4 x 5
1
8. f ( x)=
4
x5
1
9. f ( x)=
5
x4
x
10. f ( x)=
x
| BOLETÍN DE TRABAJO nº 6 10

18. +
BOLETÍN DE TRABAJO nº 7
Calcula las derivadas de las siguientes funciones
1. f ( x)= x x
2. f ( x )= x 5 x
x
3. f ( x)= 5
x
x5
4. f ( x)=
x
1
5. f ( x)=
x3 x
x
6. f ( x)=
x3 x
7. f ( x)= x 3 3 x 2
x3 3 x2
8. f ( x)=
x3
4
x5
9. f ( x)=
5
x4
x3 4 x5
10. f ( x)=
x5 5 x4
| BOLETÍN DE TRABAJO nº 7 11

19. +
BOLETÍN DE TRABAJO nº 8
Calcula las derivadas de las siguientes funciones
1
1. f ( x )= 3 x 5 − 5 x 3 −
x4
2. f ( x)= ( x )( x )
3 5 5 3
3
x5
3. f ( x)=
5
x3
x5
4. f ( x)= 3
5
x3
3
x5 − 5 x3
5. f ( x)=
3
x5 + 5 x3
1 − 3 x5
6. f ( x)=
1 + 5 x3
5
x3
7. f ( x)=
1
x4
1
8. f ( x)=
5
x3
1
9. f ( x)=
3
x5
x4
10. f ( x)=
5
x3
| BOLETÍN DE TRABAJO nº 8 12

20. +
BOLETÍN DE TRABAJO nº 9
Calcula las derivadas de las siguientes funciones
x4
1. f ( x)= 3
5
x3
5
 1 
2. f ( x)= 3 
5 3


 x 
3. f ( x)= 3 (x) 5 3
5
4. f ( x)= 5 5
x3
x3
5. f ( x)= 5
x
1− x
6. f ( x)= 3
1+ x
7. f ( x )= e
3
3
x5
8. f ( x)= e
9. f ( x)= 3 5 x
3
3 x5
10. f ( x)= 5
| BOLETÍN DE TRABAJO nº 9 13

21. +
BOLETÍN DE TRABAJO nº 10
Calcula las derivadas de las siguientes funciones
1. f ( x)= ln 3 x
2. f ( x)= lg 3 3 x
3. f ( x )= lg 3 x 3
4. f ( x)= lg 3 3 x
5. f ( x)= 3 lg3 x
3
6. f ( x )= 3 x
7. f ( x )= lg 3 3 3 x
3
3x
8. f ( x)= 3lg3
9. f ( x)= 3 lg 3 3 x
10. f ( x)= 3 ln x 3
| BOLETÍN DE TRABAJO nº 10 14

22. +
BOLETÍN DE TRABAJO nº 11
Calcula las derivadas de las siguientes funciones
1. f ( x)= ln x − e x − 3 x 2
2. ( )
f ( x)= (ln x )(− e x ) 3 x 2
ln x
3. f ( x )= x
e
ln( − x )
4. f ( x)=
3
x2
x −e − e x
5. f ( x)=
(ln x )3 x 2
1− ex
6. f ( x)=
1+ ex
1 − ln x
7. f ( x)=
1 + ln x 2
8. f ( x)=
( )
(3 x ) 3 x 2
ln x
1 + ln x
9. f ( x)= 3
1 − ln x
10. f ( x)= 3 e x( ) 2
| BOLETÍN DE TRABAJO nº 11 15

23. +
BOLETÍN DE TRABAJO nº 12
Calcula las derivadas de las siguientes funciones
f ( x)= 3 (ln e x )
2
1.
2. f ( x)= 3 e ln x
3. f ( x)= ln 3 x 2
3 2
4. f ( x )= ln e x
5. f ( x)= ln 3 e x
ln e x
6. f ( x)= 3
ex
1− x
7. f ( x)= 3
x
3 x
8. f ( x)= e e
9. f ( x)= e ln x
3
x2
10. f ( x)= e ln
| BOLETÍN DE TRABAJO nº 12 16

24. +
BOLETÍN DE TRABAJO (Ana Fraga) (no soluciones)
Deriva:
1− x2 
1. y = arcsen  2
 x 

 
π 
2. y = e − x · sen  − log x 
4 
tg x
2
3. y =  
x
 2 5−3 x 
 cos x 
4. y = ln  
 
tg 2 x 3
5. y =
e sen x
6. y = 3 x · arccos x
4
 π
7. y = 10 cos 8  7 x − 
 2
(
8. y = ln 2 2 π−3 )
1− x
9. y =
e + e−x
x
10. y = arctg 1 − x
| BOLETÍN DE TRABAJO (Ana Fraga) (no soluciones) 17

25. +
EJERCICIOS VARIOS
Fuente Ana Fraga Vila
1) Deriva las siguientes funciones:
sen x
y= 2
y = ln (3x2 − 5x) y = e−2x · cos x
x
 1+ x  sen x
y = cos3 x · cos x2 y = ln   y= 2
1− x  x
y = arcsen x y = ( tg x) x y = sen 3 x · sen x 3
 1 − 2x  x
2
y = cos   y= 3 y = xsen x
 1 + 2x  x
y = x2 · e−3x y = ln (sen 2 x) y = e−x · sen3 x
cos x 2  9x 2 − 3 
y=x y = tg x  x3 
y = ln  
 
9x 2 − 3
y= y = xsen x y = ln (ex + cos x)
x3
x2 − 3
y= 3− 5 x 2
y = (3 x 2 ) tg x y = log ( cos x + 1 − 3x 2 )
5
 1 − 2x  3 π
y=L sen ( 7 x − x 2 ) 3 y = cos   y = tg  
 1 + 2x  x
x -x
+
y = arctg (1 − x 2 ) y = e x e- x y = cos (sen x 3 )
e -e
y = x3 x y= sen 2 x + ( x 2 − 1) 3 y = arctg 6 x 3
x  1 
y= y = ln  + tg x  y = e 2 − sen 3 ( x 2 )
1 + 4x 2
 cos x 
| EJERCICIOS VARIOS 18

26. +
2 x
y = arctg x y = (e x − 1) 3 x y= 2
+ 2
( x − 1) x −4
y = ln ( x) 31
y = 2 tg   y = e − x − (cos x + sen x)
 x
y = tg2 (6x)
2) Interpretación geométrica de la derivada de una función en un punto. Determina los
puntos de la
curva y = x3 en los que la recta tangente es paralela a la recta y = 3x + 14
1
3) Halla la ecuación de la tangente a la hipérbola y = en el punto x = 3.
x
4) Halla la ecuación de la tangente a la curva y = 2x3 − 6x2 + 4 en su punto de inflexión.
5) Halla la ecuación de la tangente a la curva y = 2 x + 1 en el punto de abscisa 12.
9 2
6) )En qué puntos de la curva y = x 3 − x + 6 x + 1 la recta tangente es paralela al eje OX?
2
8
7) Calcula a y b para que y = ax + b + tenga en el punto (−2, −8) una tangente horizontal.
x
8) Halla p y q sabiendo que la función f (x) = x3 + px2 + q tiene un mínimo relativo en el
punto (2, 3).
9) Halla la ecuación de las tangentes a la curva y = x4 − 6x2 en sus puntos de inflexión.
10) Halla la ecuación de la recta tangente a la curva y = 2x3 − 6x2 + 4 en su punto de
inflexión.
| EJERCICIOS VARIOS 19

27. +
11) Dada la parábola y = x2 − x
a) Calcula la ecuación de la recta tangente en el punto de abscisa x0 = 1.
b) ¿En qué punto de la parábola la recta tangente es paralela a la recta y = −x + 3?
2x 3
12) Halla las asíntotas de la función y = 2
x −4
2
− 3x + 2
13) Asíntotas de la curva y = x2
x − 5x + 4
x2 − x − 5
14) Halla las asíntotas de f ( x) =
x
x
15) Halla los puntos de corte con los ejes y las asíntotas de y = 2
x −1
x
16) Calcula los máximos, mínimos y puntos de inflexión, si existen de la función y = 2
x −1
x3
17) Calcula las asíntotas de la función y =
( x − 4) 2
x
18) Halla las asíntotas de la curva de ecuación y = 2
x − 10 x + 9
x + x +1
2
19) Estudia el crecimiento, decrecimiento, máximos y mínimos de la función: y =
x +1
20) Intervalos de crecimiento y decrecimiento, concavidad y convexidad de la función y =
x2(3 − 2x).
21) Estudia el crecimiento, decrecimiento, extremos relativos, curvatura y puntos de inflexión
de
f ( x) = x 3 − 3 x 2 + 1 . Representarla gráficamente.
| EJERCICIOS VARIOS 20

28. +
2
+1
22) Representa gráficamente la función y = x 2
x −1
Calculando el dominio de definición, puntos de corte con los ejes, asíntotas,
intervalos de
crecimiento y decrecimiento, máximos y mínimos.
23) Esboza la gráfica de y = 3 x 2 − 6 x
24) Dada la función f ( x) = x 3 − 3 x + 7.
a) Calcula máximos, mínimos y puntos de inflexión
b) Esboza su gráfica
c) Escribe la ecuación de la recta tangente en su punto de inflexión.
1 3
25) Representa gráficamente f ( x) = − x + x 2 , hallando: puntos de corte con los ejes,
6
monotonía
(crecimiento y decrecimiento), máximos, mínimos, curvatura y puntos de inflexión.
x2
26) Estudia y representa gráficamente y = 2
x +1
27) Halla b, c y d para que la función f ( x) = x 3 + bx 2 + cx + d tenga un punto de inflexión
en x = 3,
pase por el punto (1, 0) y tenga un extremo en x = 5.
28) Representa gráficamente la función y = (2 − x)2 calculando previamente:
a) Dominio de definición.
b) Puntos de corte con los ejes.
c) Intervalos de crecimiento y decrecimiento. Máximos y mínimos.
| EJERCICIOS VARIOS 21

29. +
x
29) Dada la función f ( x ) =
1+ x2
a) Calcula: Intervalos de crecimiento y decrecimiento. Máximos y mínimos.
b) Halla sus asíntotas.
c) Esboza su gráfica
| 22

30. +
| 23

31. +
Fuente: IES Rego da auga
| 24

32. +
SOLUCIONES BOLETIN 1
1. f ( x)= 3 x 5 − 2 x 4 + 5 x 3 − 3 x − 1 → f ' ( x) = 15 x 4 − 8 x 3 + 15 x 2 − 3
2. ( )
f ( x)= (−2 x 3 )(4 x 2 ) → f ' ( x) = − 6 x 2 (4 x 2 ) + (−2 x 3 )(8 x) = −24 x 4 − 16 x 4 = −40 x 4
3. f ( x)=
3x 2
→ f ' ( x) =
(6 x )(2 x ) − (3x )(6 x ) = 12 x − 18 x
3 2 2 4 4
=
− 6x 4 −3
= 2
2x3 (2 x )
3 2 4x 6
4x 6
2x
4. f ( x)= (−2 x 3 )(2 x ) → f ' ( x) = (−6 x 2 )(2 x ) + ( −2 x 3 )(2 x ln 2)
x +1 1( x − 1) − ( x + 1)1 −2
5. f ( x)= → f ' ( x) = =
x −1 (x − 1) 2
(x − 1)2
1  1
 lg 2 e (ln x ) − (lg 2 x ) 
lg x
f ( x)= 2 → f ' ( x) =    x
x
6.
ln x (ln x ) 2
cos x −1 − senx ⋅ cos x − cos x ⋅ cos x − sen 2 x − cos 2 x
7. f ( x)= = ctgx → f ' ( x) = ⇔ f ' ( x) = =
senx sen 2 x sen 2 x sen 2 x
3x 3 x ln 3 ⋅ x 3 − 3 x 3 x 2 3 x x 2 (ln 3 ⋅ x − 3 x +1 ) 3 x (ln 3 ⋅ x − 3 x +1 )
8. f ( x)= 3 → f ' ( x)= = =
x (x 3 )2 x6 x4
1 −3
9. f ( x )= 3 = x −3 → f ' ( x ) = −3 x − 4 = 4
x x
1
0 ⋅ ln x − 1
10. f ( x)=
1
→ f ' ( x) = x = −1
2
ln x ln x x ln 2 x
| 25

33. +
SOLUCIONES BOLETIN 2
1 1 −1
1 2 −1 1 2 1 1
1. f ( x)= x = x 2 → f ' ( x) = x = x = 1 =
2 2 2 x
2x 2
−2
2. f ( x )= x − 2 → f ' ( x ) = −2 x − 2 −1 = −2 x −3 = 3
x
−2
x −5
3. f ( x)= 3 = x −5 → f ' ( x) = −5 x −5−1 = −5 x −6 = 6
x x
3 −2 −3
4. f ( x)= 2 x − 3 x → f ' ( x) = 6 x + 6 x
1
5. f ( x )= − 2 = x 2 → f ' ( x ) = 2 x
x
1 0(senx + cos x ) − 1(cos x − senx ) − (cos x − senx )
6. f ( x)= → f ' ( x) = =
senx + cos x (senx + cos x )2 (senx + cos x )2
7. f ( x)=
senx − cos x
→ f ' ( x) =
(cos x + senx )(senx + cos x ) − (senx − cos x )(cos x − senx )
senx + cos x (senx + cos x )2
−1
1 − ln x
(1 + ln x ) − (1 − ln x ) 1 −2
8. f ( x)= → f ' ( x) = x x =
1 + ln x (1 + ln x ) 2
x(1 + ln x )
2
9. f ( x)=
1− x2
→ f ' ( x) =
( ) ( )(
(− 2 x ) 1 − x −2 − 1 − x 2 2 x −3 )
1 − x −2 (
1 − x −2
2
)
10. f ( x)=
x−2 x
→ f ' ( x)=
(1 − 2 x
ln 2)(1 + 2 ) − (x − 2 )(2
x x x
ln 2)
1+ 2 x
(1 + 2 )
x 2
| 26

34. +
SOLUCIONES BOLETIN 3
e −1 0 ⋅ ln e − (e − 1) ⋅ 0
1. f ( x)= → f ' ( x) = =0
ln e (ln e )2
1
2. f ( x )= xe x − x ln x → f ' ( x ) = 1 ⋅ e x + xe x − 1 ln x − x = e x + xe x − ln x − 1
x
1
3. f ( x )= e x ⋅ ln x → f ' ( x ) = e x ⋅ ln x + e x ⋅
x
1
x e x ⋅ ln x − e x ⋅
e x
4. f ( x)= → f ' ( x) =
ln x ln 2 x
1− e x
(− e )(1 + ln x ) − (1 − e ) 1 
x
 
x
5. f ( x)= → f ' ( x) =
x  
1 + ln x (1 + ln x ) 2
1
6. f ( x )= (1 − ln x )( x + e x ) → f ' ( x ) = (− )( x + e x ) + (1 − ln x )(1 + e x )
x
e −1
7. f ( x)= x → f ' ( x) = ex
e
8. f ( x)= x e ⋅ e x → f ' ( x) = ex e −1 ⋅ e x + x e ⋅ e x
9. f ( x)=
1+ ex
→ f ' ( x) =
(e x )(1 − e x ) − (1 + e x )(− e x )
1− ex (1 − e x )2
1 x 1
ln x − e x
x  x
( x
 − e  ln x + e − ln x − e  + e  ) ( )
→ f ' ( x) =   x 
x
10. f ( x)=
ln x + e x
ln x + e x 2
( )
| 27

35. +
SOLUCIONES BOLETIN 4
1. f ( x)= x 3 ⋅ 3 x → f ' ( x) = 3 x 2 ⋅ 3 x + x 3 ⋅ 3 x ln 3
1 
3 x ln 3(lg 3 x ) − 3 x  lg 3 e 
3 x
x 
2. f ( x)= → f ' ( x) =
lg 3 x (lg 3 x ) 2
 x 1  x  x 1 
3 + lg 3 x
x ( ) ( )
 3 ln 3 + lg 3 e  3 − lg 3 x − 3 + lg 3 x  3 ln 3 − lg 3 e 
x
→ f ' ( x) =    
x x
3. f ( x)= x
3 − lg 3 x 3 − lg 3 x
x 2
( )
4. f ( x)= senx ⋅ tgx → f ' ( x) = cos x ⋅ tgx + senx ⋅ (1 + tg 2 x)
2
5. f ( x)=
senx
(= cos x ) → f ' ( x) = cos x ⋅ tgx − senx ⋅ (1 + tg x) = .... = − senx
tgx tg 2 x
6. f ( x)=
x − senx
→ f ' ( x) =
(1 − cos x )(x + cos x ) − (x − senx )(1 − senx )
x + cos x (x + cos x )2
7. f ( x)=
cos x − senx
→ f ' ( x) =
(
(− senx − cos x )(tgx + cos x ) − (cos x − senx ) (1 + tg 2 x) − senx )
tgx + cos x (tgx + cos x )2
 1
cos x ⋅ senx
(− sen 2
)
x + cos 2 x (tgx ⋅ cos x ) − (cos x ⋅ senx ) 2
⋅ cos x + tg 2 x ⋅ (− senx
8. f ( x)= → f ' ( x) =  cos x
tgx ⋅ cos x (tgx ⋅ cos x ) 2
9. f ( x)=
cos x − 1
→ f ' ( x) =
(
(− senx − 1)(tgx + x ) − (cos x − 1) 1 + tg 2 x + 1 )
tgx + x (tgx + x )2
10. f ( x)=
x − senx
→ f ' ( x) =
(1 − cos x )(x + cos x ) − (x − senx )(1 − senx )
x + cos x (x + cos x )2
| 28

36. +
SOLUCIONES BOLETIN 5
1
1. f ( x)= x 3 − 3 x − 3 x → f ' ( X ) = 3 x 2 − 3 x ln 3 −
3⋅ 3 x2
2. f ( x)= ( x )(3 ) → f ' ( x) = 
3 x
3


 x 3
2 
1
 3 + x 3 x ln 3 ( ) ( )( )
 3⋅ x 
1
 lg 3 e (3 ) − (lg 3 x )(3 ln 3)
 x x
lg x
f ( x)= 3x → f ' ( x) =  
x
3.
3 (3 x )2
ln x 1
4. f ( x)= 3 → f ' ( x ) = 3
3 3 ⋅x
 1  1 
(3x 2
)( ) ( ) 
− 3 x ln 3 (lg 3 x )3 x − x 3 − 3 x   lg 3 e 3 x + (lg 3 x )
 x  3 2


x3 − 3x    3⋅ x 
5. f ( x)= → f ' ( x) =
(lg 3 x )3 x ((lg 3 x )3 x )
2
6. f ( x)=
1 − x3
→ f ' ( x) =
(3x 2 )(1 + 3 x ) − (1 − x 3 )(3 x ln 3)
1 + 3x (1 + 3 x )2
1 1 
 (1 + lg 3 x ) − (1 − ln x ) lg 3 e 
1 − ln x
→ f ' ( x) =   x 
x
7. f ( x)=
1 + lg 3 x (1 + lg 3 x ) 2
 1 
8. ( ) ( ) ( )
f ( x)= x 3 (− 3 x ) 3 x → f ' ( x) = (3x 2 )(− 3 x ) 3 x + (x 3 )(− 3 x ln 3) 3 x + (x 3 )(− 3 x )
 3 2

 3⋅ x 
 1  1 
 1 + (x − lg 3 x ) − ( x + ln x )1 − lg 3 e  
x + ln x 1  x  x 
9. f ( x)= 3 → f ' ( x) =
2  
x − lg 3 x  x + ln x   (x − lg 3 x ) 2

 x − lg x  
33   
 3 
x
 3x

3
 3 ln 3  ⋅ 1
10. f ( x)= 3 = 3 → f ' ( x) = 
x 3
 3
 
| 29

37. +
SOLUCIONES BOLETIN 6
1. f ( x)= 3 x 5 → f ' ( x) = 15 x 4
2. f ( x)= x 15 − x → f ' ( x) = 15 x14 − 1
1 −2
3. f ( x )= 2 = x − 2 → f ' ( x ) = −2 x −3 = 3
x x
3
x −2
4. f ( x)= 5 = x −2 → f ' ( x) = −2 x −3 = 3
x x
x −1 −4 5
5. f ( x )= 5 = x − 4 − x −5 → f ' ( x ) = −4 x −5 + 5 x −6 = 5 + 6
x x x
1
4 4 − 5
6. f ( x)= 5 x 4 = x 5 → f ' ( x) = x 5 = 5
5 5 x
5 1
4 5 5 54 x
7. f ( x)= x = x → f ' ( x) = x 4 =
4
4 4
−5 −9
1 −5 4 −5
8. f ( x)= = x 4 → f ' ( x) = x =
4
x 5 4 4 x9
4
−4 −9
1 −4 5 −4
9. f ( x)= =x 5
→ f ' ( x) = x =
5
x4 5 55 x 9
1 1
x 1− 1
10. f ( x)= =x 2
= x 2 → f ' ( x) =
x 2 x
| 30

38. +
SOLUCIONES BOLETIN 7
1 3 3 1
1+ 3 2 −1 3 2 3
1. f ( x)= x x = x 2
= x 2 → f ' ( x) =
x = x = x
2 2 2
1 11 11 9
5
5+ 11 2 −1 11 2 11 9
2. f ( x)= x x = x 2
= x → f ' ( x) = x
2
= x = x
2 2 2
1 −9 −9 −11
x −5 − 9 2 −1 − 9 2 −9
3. f ( x)= 5 = x 2 = x 2 → f ' ( x) = x = x =
x 2 2 2 x 11
1 9 9 7
x5 5− 9 −1 9 9 7
4. f ( x)= =x 2
= x → f ' ( x) = x 2 = x 2 =
2
x
x 2 2 2
1 −4 −4 −7
1 −1− − 4 3 −1 − 4 −4
5. f ( x)= =x 3
=x 3
→ f ' ( x) = x = x 3
=
x x 3
3 3 3 x73
1 −5 −5 −7
x 1− 3− − 5 2 −1 − 5 −5
6. f ( x)= =x 2
= x 2 → f ' ( x) = x = x 2
=
x 3
x 2 2 22 x 7
2 11 11 8
33 2
3+ 11 −1 11 11
7. f ( x)= x x =x 3
=x 3
→ f ' ( x) = x 3 = x 3 = 3 x 8
3 3 3
2 3 22−9 13 13 7
x3 3 x 2 3+ − 13 −1 13 −56 7
8. f ( x)= =x 3 2
=x 6
=x 6
→ f ' ( x) = x 6 = x 6 = x
x3 6 6 2
5 4 25−16 9 9 −11
4
x5 − 9 20 −1 9 20 9
9. f ( x)= =x 4 5
=x 20
=x 20
→ f ' ( x) = x = x =
5
x4 20 20 20 11
20 x
5 4 25−16 −39 −39 −59
x3 4 x5 3+ −5− −2+ − 39 20 −1 − 39 20 − 39
10. f ( x)= =x 4 5
=x 20
=x 20
→ f ' ( x) = x = x =
x5 5 x 4 20 20 2020 x 59
| 31

39. +
SOLUCIONES BOLETIN 8
5 3 2 −2
3 1 5 −45 5 3 3 5
3 −5 52 x 3 3 4
1. f ( x)= x − x − 4 = x − x − x → f ' ( x) = x − x + 4 x =
3 5
− + 5
x 3 5 3 5
5 x 2 x
( x )( )  5  5 
3 34 19
34 15 3415 x 34
2. f ( x)= 3 5 5
x =  x  x  = x → f ' ( x) = x =
3

3 

15
   15 15
5
3 5 16 1
x x 3
16 15 1615 x
3. f ( x)= = 3
=x 15
→ f ' ( x) = x =
5
x3 5
15 15
x
1
1 1
 5
5  3  5− 3  3  22  3 22 7 15 7
f ( x)= 3
x x
= 3
  x 5  =  x 5  = x 15 → f ' ( x) = 22 x 15 = 22 x
4.
5 3
 5 =
    15 15
x
x     
3
 52 x 3

 3
−
3 3 5 5 3
55 x 2 
 2 3
 x + x − 3 x5 − 5 x3  5 x + 3
 3 55 x 2
( )( ) 


x5 − 5 x3
5. f ( x)= → f ' ( x) =    
3
x5 + 5 x3 3
x5 + 5 x3
2
( )

−
3
 5 2

( )(
 52 x 3
 1 + 5 x3 − 1 − 5 x3 
  3
) 


1 − 3 x5  5 x   −
6. f ( x)= → f ' ( x) =
1 + 5 x3 (1 + x ) 5 3
2
3 23 18
5
x3 23 5 235 x18
7. f ( x)= = x 4 x 5 = x 5 → f ' ( x) = x =
1 5 5
4
x
−3 −8
1 −3 5 −3
8. f ( x)= = x → f ' ( x) =
5
x =
5
x3 5 55 x 8
−5 −8
1 −5 3 −5
9. f ( x)= = x 3 → f ' ( x) = x =
3
x5 3 3 x8
3
3 17 12
x4 4− 17 5 175 x12
10. f ( x)= =x 5
= x 5 → f ' ( x) = x =
5
x3 5 5
| 32

40. +
SOLUCIONES BOLETIN 9
1
1 1
4  4  3  4− 3  3  17  3 17 2
x x  17 1715 x 2
1. f ( x)= 3 = 3  =  x 5  =  x 5  = x 15 → f ' ( x) = x 15 =
   
5
x 3
 5      15 15
x 
1
 1 
5  5 3 1
 1  −1
2. f ( x)= 3  
5 3  =  3  = x −3 ( ) 3 = x −1 → f ' ( x) = − x − 2 =
 x   5 ⋅5  x2
x 
1
(x)
5
 3
( )
5
3. f ( x)= 3 5 3
=  x3

5
 = x → f ' ( x) = 1

 
1
− 22
 5 5
3 3
4. f ( x )= 5 5 3
 x  = x 25 → f ' ( x ) = 3 x 25 =
x = 
3
  25 25 22
25 x
1
1
 3
5  5 5
3 1

x x 1
5. f ( x)= 5  =  x 2  = x 2 = x → f ' ( x) =
= 1  
 x  2   2 x
 x
1− x
−2  − 1 


1 1− x  3  2 x  
 1 
 1+ x − 1− x 
 
 ( ) ( )
6. f ( x)= 3 → f ' ( x) =    2 x 
1+ x 3 1+ x   1+ x
2
( )
7. f ( x)= 3 e → f ' ( x) = 0
3
x5
3
x5 53 2
8. f ( x )= e → f ' ( x) = e x
3
x x
1
9. f ( x)= 3 5 x = 5 3 → f ' ( x) = 5 3 ⋅ ln 5 ⋅
3
1
9
−4 x5
 3 3
5 5 5
3 3 5 5 5 ⋅ ln 5 ⋅ 5
= 5x  = 5 x → f ' ( x) = 5 x ln 5 ⋅ x 9 =
9 9
10. f ( x)= 5 x
 
  9 99 x 5
| 33

41. +
SOLUCIONES BOLETIN 10
1  1
1. f ( x)= 3 lg 3 3 x → f ' ( x) =
 x
(
 x lg 3 e  ⋅ 3 ln 3 )
(
33 lg 3 3 )
x 2 3 
1  1  2
2. f ( x)= 3 ln x 3 → f ' ( x) =  3  3x ( )
3
3 ln x ( )
3 2 x 
 1  1 
3. f ( x)= lg 3 3 x → f ' ( x) =  3 lg 3 e 
  3 2  
 x  3 ⋅ x 
 1 
4. f ( x)= lg 3 3 x → f ' ( x) =  x lg 3 e (3 x ln 3)
3 
 1 
5. f ( x)= ln 3 x → f ' ( x) =  x (3 x ln 3)
3 
 1 
6. f ( x)= lg 3 x 3 → f ' ( x) =  3 lg 3 e (3 x 2 )
x 
7. f ( x)= lg 3 3 3 x → f ' ( x) = 
 1
3 x
 1
lg 3 e  3 3 x ln 3  
 3
( )
 3 
1
( )
8. f ( x)= 3 lg3 x → f ' ( x) = 3lg3 x ln 3  lg 3 e 

x 
3
(3
9. f ( x)= 3 x → f ' ( x) = 3 x ln 3 
 1 
 3 2 ) 
 3⋅ x 
3 x
( 3 x
10. f ( x)= 3lg3 3 → f ' ( x) = 3lg3 3 ln 3 
 1
3 x ) 1
lg 3 e  3 3 x ln 3  
 3
( )
 3 
| 34

42. +
SOLUCIONES BOLETIN 11
1 2
1. f ( x)= ln x − e x − 3 x 2 → f ' ( x) = − ex − 3
x 3 x
2. f ( x)= (ln x ) − e x ( )(
3
x2 ) 1
 x
( ) ( ) 2 
→ f ' ( x) =  (− e x ) 3 x 2 + (ln x )(− e x ) 3 x 2 + (ln x )(− e x ) 3  →
 
3 x 
1 x
e − ln x ⋅ e x
ln x
3. f ( x)= x → f ' ( x) = x
e ex
2
( )
ln(− x)
 1

−x


( )  2 
(−1)  3 x 2 + (ln(− x) ) 3 
 
3 x 
4. f ( x)= → f ' ( x) =
3
x2 (x) 3 2
2
− e )((ln x )( x )) − (x − e ) ( x ) + ln x
1  2 
(− ex − e −1 x 3
x
2 −e
 

x 3 2
x −e
−e x
  3 x 
3
5. f ( x)= → f ' ( x) =
(ln x )3 x2 ((ln x) x ) 3 2
2
1− ex − e x (1 + e x ) − (1 − e x )(e x )
6. f ( x)= → f ' ( x)=
1+ ex (1 + e x )2
1  1
1 − ln x
( 
  1 + ln x − (1 − ln x ) 2 2 x 
2
)
→ f ' ( x)=   x 
x
7. f ( x)=
1 + ln x 2
1 + ln x 2 2
( )
(3 )( x 3 2
)
 x
 3 ln 3( )( 3
)  2 
 ( )
x 2 + 3 x  3  (ln x ) − 3 x

 3 x 
(( )( x )) 1 
3 2
x
→ f ' ( x)= 
x
8. f ( x)=
ln x (ln x )2
1 + ln x 1  1 + ln x 
−2
 1 1 
 
 x 2 x 
(  ) (
 −1 1  
 1 − ln x − 1 + ln x  
 )
9. f ( x)= 3 → f ' ( x)=  
3
 x 2 x 
1 − ln x 3  1 − ln x 
 



1 − ln x
2
( 


)
 
2x 2x
2
10. f ( x)= 3
(e ) x 2
=e 3
→ f ' ( x) = e 3
⋅
3
| 35

43. +
SOLUCIONES BOLETIN 12
[( ) ] [2(ln e ) ]e1 e ] [2(ln e ) ]
−2 −4
(
f ( x)= 3 ln e x )
2
→ f ' ( x) =
1
3
ln e x
2 3 x 1
x
x
=
1
3
[
ln e x 3 x 1
1. 2 −1
2 3 2
(
f ( x)= 3 ln e x )
2
= 3 (x ) = x 3 → f ' ( x) =
2
3
x = 3
3 x
1 ln x −32 ln x 1
2. f ( x)= 3 e ln x → f ' ( x) =
3
e e ( )x
−1
1 2 3 2 2 2
3. f ( x)= ln 3 x 2 → f ' ( x) = ⋅ x = = =
3
x2 3 33 x 2 3 x 33 x 3 3x
−1
3 2
1 2 3 2
4. f ( x)= ln e → f ' ( x) = 3 2 e ⋅ x 3
x x
e x 3
1 3 x 1
5. f ( x)= ln 3 e x → f ' ( x) = e ⋅
3
ex 3
−2  1  −2
 ⋅ e ⋅ e − ln e ⋅ e
x x x x

ln e x 1  ln e x  3  e x = 1  ln e x  3  1 − ln e x 
6. f ( x)= 3 x → f ' ( x) =  x     
e 3 e  
   (e x )2  3  ex



 ex




 
−2
1− x 1  1 − x  3  − x − (1 − x ) 
7. f ( x )= 3 → f ' ( x) =    
x 3 x   x2 
3 x 3 x 1
8. f ( x )= e e → f ' ( x ) = e e 3 e x ⋅
3
1
9. f ( x )= e ln x → f ' ( x ) = e ln x ⋅
x
−1
3
ln x 2
3
ln x 2 1 2 3
10. f ( x)= e → f ' ( x) = e ⋅ ⋅ x
3
x2 3
| 36

44. +
SOLUCION PROBLEMAS ANA FRAGA
2) (1, 1) , (−1, −1)
1 1
3) y− = − (x − 3)
3 9
4) y = −6(x − 1)
1
5) y−5= (x − 12)
5
6) (1, 3,5) , (2, 3)
7) a = 2, b = 0
8) p =−3; q = 7
9) y + 5 = 8(x + 1), y + 5 = −8(x − 1)
10) y = −6(x − 1)
11) a) y = x − 1 b) (0, 0)
12) x = 2, x = −2, y = 2x
13) x = 4, y=1
14) x = 0, y=x−1
15) (0, 0), x = −1, x = 1, y=0
16) Punto de inflexión (0, 0)
17) x = 4, y = x + 8
18) x = 1, x = 9, y=0
19) Creciente en ]−∞, −2[ ∪ ]0, +∞[. Decreciente en ]−2,−1[ ∪ ]−1, 0[. Mínimo (0, 1).
Máximo (−2,−3)
20) Creciente en ]0, 1[. Decreciente en ]−∞, 0[ ∪ ]1, +∞[.
Convexa en ]−∞, 1 / 2 [. Cóncava ] 1 / 2 , +∞ [
| 37

45. +
21) Creciente en ]−∞,0[ ∪ ]2,+ ∞ [. Decreciente en ]0, 2[. Mínimo (2, −3). Máximo (0, 1)
Convexa en ]1, +∞[. Cóncava ]−∞, 1[. Punto de inflexión (1, −1)
22) 24)
24) a) Mínimo (1, 5). Máximo (−1, 9). Punto de inflexión (0, 7)
b)
c) y − 7 = −3x
25) 26)
27) b = −9, c = 15, d = −7
| 38

46. +
28) a) D = R; b) (0, 4) (2, 0) c) Decreciente en ]− ∞, 2[ ; Creciente en ]2, +∞[.
Mínimo (2, 0)
29) a) Creciente en ]−1, 1[. Decreciente en ]−∞, 1[ ∪ ]1, +∞[. Máximo (1, 1 / 2 ), mínimo
(−1, − 1 / 2 )
b) y = 0
| 39

47. +
U⌀ℕℤℚ∊ℝℂℙℐΩ⇐⇒⇔⇏∊∉∈∅⇾≈≔⇎⇝≡ℤ≤≥≲≳≴≵≮≯∀⇒∊≠∅⊂⟇·∃
A⨯Bεαβηθλµξσφφδεε
·∅U∩∪∼∿⊂⊃⊆⊇⊄⋂⋃⊅∧∨U⤳≮≠|∂∆√±∞ǀǁƟƩǃξχ∘6⊕⊗⊛⋅♫♯
⨁⨂✘✔×
| 40