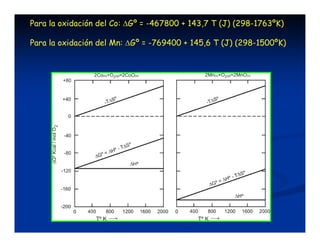
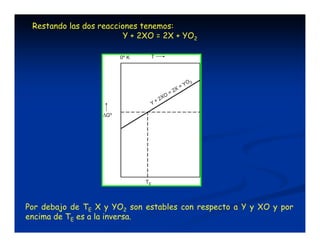
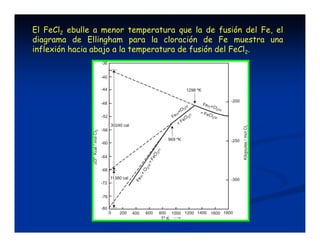
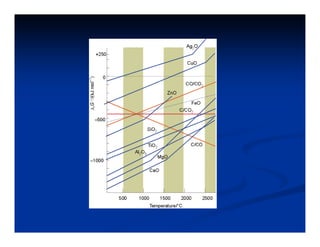
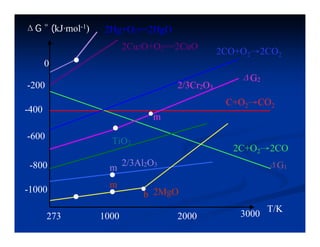
El documento describe los diagramas de Ellingham, que muestran la relación entre la variación de la energía libre estándar (ΔG°) de reacciones de oxidación y la temperatura. Ellingham observó que estas relaciones se aproximaban a rectas en rangos de temperatura donde no ocurrían cambios de fase. Los diagramas permiten predecir la estabilidad termodinámica relativa de óxidos a diferentes temperaturas.

1. Diagramas de Ellingham

2. Diagramas de Ellingham
Ellingham graficó las relaciones ΔΔV-T determinadas
experimentalmente para la oxidación y sulfuración de una serie de
metales y encontró que estas en forma general se aproximaban a
rectas en un rango de temperaturas en el cual no se producían
cambios de estado.
y = m ⋅ x +
b
G S T H
Δ = −Δ ⋅ + Δ

3. La figura es el diagrama de Ellingham para la reacción de oxidación
4 Ag(s) + O2(g) = 2Ag2O (s)
ΔHº es la intersección de la línea con el eje T=0 y ΔSº es la pendiente de la
línea cambiada de signo. Como ΔSº es una cantidad negativa la línea tiene
pendiente positiva.

4. A la temperatura de 462ºK el ΔGº de la reacción es cero, o sea
que a esa temperatura Ag sólida pura y oxígeno gas a 1 atm están
en equilibrio óxido de Ag puro y p O2(eq,T) =1.
A T1 el ΔGº para la reacción es negativo y el óxido es más estable, a T2
el ΔGº para la oxidación es positivo y por lo tanto son más estables la
Ag y el oxígeno.

5. Para la oxidación del Co: ΔGº = -467800 + 143,7 T (J) (298-1763ºK)
Para la oxidación del Mn: ΔGº = -769400 + 145,6 T (J) (298-1500ºK)

6. Consideremos dos reacciones de oxidación:
2X + O2 = 2XO (1) y Y + O2 = YO2 (2)
En la figura se puede apreciar que ΔHº (2) es más negativa que ΔHº
(1) y que ΔSº (2) es más negativa que ΔSº (1) .

7. Restando las dos reacciones tenemos:
Y + 2XO = 2X + YO2
Por debajo de TE X y YO2 son estables con respecto a Y y XO y por
encima de TE es a la inversa.

8. Richardson añadió otra escala a los diagramas de Ellingham.
A cualquier temperatura la variación en energía libre estándar
está dada por:
( ., )
º
2 ln O eq T ΔG = −RT p
pero
G = Gº + RT ln P
por lo tanto ΔGº puede ser vista como el descenso en la energía libre
de un mol de oxígeno(g) cuando su presión decrece de 1 atm a P O2 (eq,T)
atm a la temperatura T.
Para una disminución de presión de un mol de un gas ideal ΔG es
una función lineal de la temperatura y la pendiente de la recta es
R ln P, por lo tanto ΔG se volverá más negativo con la
temperatura si P<1 y más positivo si P>1. Todas las líneas partiran
de ΔG= 0 y T= 0.

9. ( ., )
º
2 ln O eq T ΔG = −RT p

10. A T1 ΔGº = ab la disminución en energía libre a T1 cuando pO2 disminuye de 1
a 10-20 y por lo tanto la presión de oxígeno en el equilibrio será = 10 -20
A T3 ΔGº = 0, que corresponde al estado en el que no hay cambio en la
presión, la presión de oxígeno en el equilibrio sera = 1
2X + O2 = 2XO (1)
Y + O2 = YO2 (2)
A cualquier temperatura menor
que TE (T1) por ejemplo
O2 (eq., reac.2, T1 ) O2 (eq,reac.1,T1 ) p < p
Ambos metales en un sistema
cerrado en una atmósfera de
O a 1 atm de presión se
oxidarán espontáneamente.

11. EFECTO DE LA TRANSFORMACIÓN DE FASES
En el rango de temperatura en el cual no ocurren cambios de fases en
ninguno de los reactantes o productos, la relación ΔGº versus T para la
reacción se puede representar aproximadamente por una línea recta.
Sin embargo, cuando la entalpía de una fase de alta temperatura
excede la de la fase de baja temperatura en una cantidad igual al
calor latente del cambio de fase y similar para la entropía que
difieren en la entropía de cambio de fase, la línea de Ellingham
presenta una inflexión.
Consideremos la reacción
X (s) + O 2(g) = XO 2(s)
para la cual el cambio en entalpía estándar es ΔHº y el cambio en
entropía estándar es ΔSº.

12. A la temperatura de fusión de X, Tm,x, se produce la reacción
X (sólido) = X (líquido)
El cambio en entalpía estándar (calor latente de fusión) es ΔHºm,x y el
correspondiente cambio en entropía es ΔSºm,x=ΔHºm,x/Tm,x.

13. La línea de Ellingham para la oxidación de X líquida a XO2 sólido tiene mayor
pendiente que la correspondiente a la oxidación de X sólido.
A Tm,x la línea presenta una inflexión hacia arriba.
No hay discontinuidad ya que a Tm,x Gºx(s) = Gºx(l).

14. La siguiente figura muestra la forma de las líneas de Ellingham
(a) Tm,x, < Tm,xO2 y (b) Tm,x, > Tm,xO2

15. El Cobre es un metal que funde a menor temperatura que su óxido de
menor punto de fusión Cu2O. Mediciones de presiones de oxígeno en
equilibrio con Cu (s) y Cu2O (s) en el rango de temperaturas de
estabilidad del Cu (s) , y en equilibrio con Cu (l) y Cu2O (s) en el rango
de estabilidad de Cu (l) se tiene:
ΔGº = -338900-14,2T lnT+247.T (J) (1)
para 4Cu (s) + O 2(g) = 2Cu2O (s) en el rango 298 – Tm,Cu
ΔGº = -390800-14,2T lnT+285,3.T (J) (2)
para 4Cu (l) + O 2(g) = 2Cu2O (s) en el rango Tm,Cu – 1503ºK

16. Esas dos líneas se intersectan a 1356ºK que corresponde al punto de
fusión del cobre (Tm,Cu).

17. El FeCl2 ebulle a menor temperatura que la de fusión del Fe, el
diagrama de Ellingham para la cloración de Fe muestra una
inflexión hacia abajo a la temperatura de fusión del FeCl2.

18. OXIDOS DE CARBONO
Existen dos formas gaseosas de óxidos de carbono:
C (gr) +O 2(g) = CO 2(g) (1) ΔGº(1)=-394100-0,84T
2 C(gr)+O 2(g) = 2CO (g) (2) ΔGº(2)=-223400-175,3T
Combinando (1) y (2)
2CO (g) +O 2(g) = 2CO 2(g) (3) ΔGº(3)=-564800+173,62T

19. 2CO+O2→2CO2
1000 2000 T (ºK)
-200
-400
-600
C+O2→CO2
2C+O2→2CO
ΔG º (kJ·mol-1)

21. Diagrama
de
Ellingham

22. ΔG º (kJ·mol-1) 2Hg+O2==2HgO
0
-200
-400
-600
-800
-1000
2Cu2O+O2==2CuO 2CO+O2→2CO2
ΔG2
2/3Cr2O3
m
C+O2→CO2
2C+O2→2CO
●
●
TiO2
2/3Al2O3
b 2MgO
●
m
●
m
●
●
●
ΔG1
273 1000 2000 3000 T/K

23. Oxidación：un elemento reacciona con el oxígeno para
producir un óxido.
Zn(g) + ½ O2(g) ZnO(s)
Reducción：un óxido se transforma en metal
MgO(s) + C (s) Mg(s) + CO(g)
Los metales se obtienen a partir de menas minerales usando
reductores (reactivos químicos) a altas temperaturas y
también por electrólisis.

24. Aspectos termodinámicos de la extracción
ΔG 0= -RT lnK
ΔG 0< 0 y K > 1
Reacción “ favorable”
(a) C (s) + ½ O2 (g) → CO (g) ΔG0
(C, CO)
(b) ½ C (S) + ½ O2 (g) → ½CO2 (g) ΔG0
(C, CO2)
(c) CO (g) + ½ O2 (g) → CO2 (g) ΔG0
(CO, CO2)
(d) xM ( sólido o líquido) + ½ O2 (g) → MxO (s) ΔG0
(M, MxO)

25. (a-d) MxO (s) + C (s) → xM (sólido o líquido) + CO(g)
ΔG0
(C, CO) - ΔG0
(M, MxO)
(b-d) MxO (s) + ½ C (s) → xM (sólido o líquido) + ½ CO2 (g)
ΔG0
(C, CO2) - ΔG0
(M, MxO)
(c-d) MxO (s) + CO (g) → xM (sólido o líquido) + ½ CO2 (g)
ΔG0
(CO, CO2) - ΔG0
(M, MxO)

26. MxO (s) + C (s) → xM (sólido o líquido) + CO(g)
ΔG0
(C, CO) - ΔG0
(M, MxO) <0 Reacción espontánea