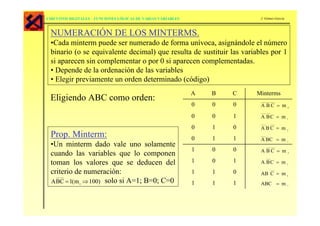
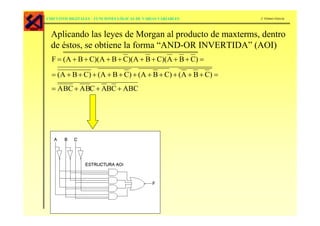
La función lógica puede expresarse de varias formas como tabla de verdad, expresión algebraica booleana, suma de productos o producto de sumas. Cualquier función lógica se puede implementar mediante circuitos de dos niveles utilizando puertas AND-OR, OR-AND, NAND-NAND, NOR-NOR o AOI. Las puertas NAND y NOR son conjuntos autosuficientes para implementar cualquier función lógica.

1. CIRCUITOS DIGITALES – FUNCIONES LÓGICAS DE VARIAS VARIABLES J. Gómez-García
Tema 3:
Funciones Lógicas

2. CIRCUITOS DIGITALES – FUNCIONES LÓGICAS DE VARIAS VARIABLES J. Gómez-García
FORMAS DE EXPRESAR UNA FUNCIÓN LÓGICA:
• Tabla de verdad forma única
• Expresión algebraica (Booleana) múltiples expresiones
equivalentes.
• Necesidad de encontrar un fórmula de paso de una a otra forma.
Teoremas:
• Toda función lógica puede expresarse como suma de productos
de las variables de las que depende (o de sus conjugados).
• Toda función lógica puede expresarse como producto de sumas
de las variables de las que depende (o de sus conjugados).
Ejemplo:
f (A, B, C, D) = (A + BC)(B + CD) = AB + ACD + BCB + BCCD = AB + ACD + BC
Suma de Productos
f (A, B, C, D) = (A + BC)(B + CD) = (A + B)(A + C)(B + C)(B + D)
Producto de sumas

3. CIRCUITOS DIGITALES – FUNCIONES LÓGICAS DE VARIAS VARIABLES J. Gómez-García
Ampliación de los teoremas:
• Toda función lógica puede expresarse como suma de productos
de todas las variables de las que depende (o de sus conjugados)
• Toda función lógica puede expresarse como producto de sumas
de todas las variables de las que depende (o de sus conjugados)
Ejemplos:
f (A, B, C, D) = AB + A CD + BC = AB(C + C) + A CD(B + B) + BC(A + A) =
= ABC( D + D) + ABC(D + D) + ABCD + A BCD + ABC(D + D) + ABC(D + D) =
= ... = ABCD + ABCD + ABCD + ABCD + A BCD + ABCD + ABCD;
Suma de productos completos o suma de minterms
f (A, B, C, D) = (A + B)(A + C)(B + C)(B + D) =
= (A + B + CC)(A + BB + C)(A A + B + C)(A A + B + D) =
= (A + B + C + DD)(A + B + C + DD)(A + B + C + DD)(A + B + C + DD)
(A + B + C + DD)(A + B + C + DD)(A + CC + B + D)(A + CC + B + D) =
= (A + B + C + D)(A + B + C + D)(A + B + C + D)(A + B + C + D)
(A + B + C + D)(A + B + C + D)(A + B + C + D)(A + B + C + D)
( A + B + C + D)
Producto de sumas completas o maxterms

4. CIRCUITOS DIGITALES – FUNCIONES LÓGICAS DE VARIAS VARIABLES J. Gómez-García
NUMERACIÓN DE LOS MINTERMS.
•Cada minterm puede ser numerado de forma unívoca, asignándole el número
binario (o se equivalente decimal) que resulta de sustituir las variables por 1
si aparecen sin complementar o por 0 si aparecen complementadas.
• Depende de la ordenación de las variables
• Elegir previamente un orden determinado (código)
A B C Minterms
Eligiendo ABC como orden:
0 0 0 A BC = m 0
0 0 1 A BC = m 1
0 1 0 ABC = m 2
Prop. Minterm: 0 1 1 A BC = m 3
•Un minterm dado vale uno solamente
1 0 0 A BC = m
cuando las variables que lo componen 4
toman los valores que se deducen del 1 0 1 A BC = m 5
criterio de numeración: 1 1 0 AB C = m 6
A BC = 1(m ⇒ 100) solo si A=1; B=0; C=0
4 1 1 1 ABC = m 7

5. CIRCUITOS DIGITALES – FUNCIONES LÓGICAS DE VARIAS VARIABLES J. Gómez-García
Expresión de una función lógica como suma de Minterms:
• Toda función lógica puede expresarse como suma de minterms a partir de su
tabla de verdad sin más que incluir en su desarrollo todos los minterms para
los cuales la función vale 1.
011 100 101 110
A B C Minterms F = ABC + A BC + A BC + ABC
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 0 F(A, B, C) = ∑ m(3,4,5,6) =
= m3 + m 4 + m5 + m6 =
= ABC + A BC + A BC + ABC

6. CIRCUITOS DIGITALES – FUNCIONES LÓGICAS DE VARIAS VARIABLES J. Gómez-García
NUMERACIÓN DE LOS MAXTERMS.
• Cada maxterm puede ser numerado de forma unívoca, asignándole el
número binario (o se equivalente decimal) que resulta de sustituir las
variables por 0 si aparecen sin complementar o por 1 si aparecen
complementadas.
•Depende de la ordenación de las variables
•Elegir previamente un orden determinado (código)
Eligiendo ABC como orden: A B C Maxterms
0 0 0 A + B+ C = M 0
0 0 1 A + B+ C = M
Prop. Maxterm: 1
•Un maxterm dado vale cero solamente 0 1 0 A + B+ C = M 2
cuando las variables que lo componen 0 1 1 A + B+ C = M 3
toman los valores que se deducen del 1 0 0 A + B+ C = M 4
criterio de numeración: 1 0 1 A + B+ C = M
A + B + C = 0( M ⇒ 011) sólo si A=0; B=1;
5
A + B+ C = M
3
1 1 0
C=1 6
1 1 1 A + B+ C = M 7

7. CIRCUITOS DIGITALES – FUNCIONES LÓGICAS DE VARIAS VARIABLES J. Gómez-García
Expresión de una función lógica como producto de Maxterms:
•Toda función lógica puede expresarse como producto de maxterms a partir de
su tabla de verdad sin más que incluir en su desarrollo todos los maxterms
para los cuales la función vale 0.
000 001 010 111
F = (A + B + C) ·(A + B + C) ·(A + B + C) ·(A + B + C)
A B C Maxterms
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 0
F ( A , B , C ) = Π M ( 0 ,1, 2 , 7 ) = M 0 · M 1 ·M 2 ·M 7 =
= ( A + B + C )( A + B + C )( A + B + C )( A + B + C )

8. CIRCUITOS DIGITALES – FUNCIONES LÓGICAS DE VARIAS VARIABLES J. Gómez-García
Propiedades de los desarrollos:
•Los minterms que aparecen en el desarrollo como suma de productos no aparecen
como maxterms en el desarrollo como producto de sumas (y viceversa).
•Los minterms (maxterms) que aparecen en el desarrollo de una función como suma
de productos (producto de sumas) no aparecen en el desarrollo de su complementaria.
Conversión de minterms a maxterms:
-Reemplazar el símbolo de minterm por el de maxterm.
-Reemplazar los índices de los minterm por los índices no usados.
F( A, B, C) = Σm(3,4,5,6) = ΠM (0,1,2,7)
Conversión de maxterms a minterms:
-Reemplazar el símbolo de maxterm por el de minterm.
-Reemplazar los índices de los maxterm por los índices no usados.
F( A, B, C) = ΠM (0,1,2,7) = Σm(3,4,5,6)
Desarrollo de F a partir del desarrollo de F :
-Emplear para F los minterms (o maxterms) no usados en F
F( A, B, C) = Σm(3,4,5,6) = F(A, B, C) = Σm(0,1,2,7) =
Π M (0,1,2,7) ΠM (3,4,5,6)

9. CIRCUITOS DIGITALES – FUNCIONES LÓGICAS DE VARIAS VARIABLES J. Gómez-García
Estructuras de dos niveles:
El desarrollo de una función como suma de minterms o producto
de maxterm conduce en ambos casos a una estructura de puertas
de dos niveles: AND-OR u OR-AND, respectivamente.
F = ABC + A BC + A BC + ABC F = (A + B + C)(A + B + C)(A + B + C)(A + B + C)

10. CIRCUITOS DIGITALES – FUNCIONES LÓGICAS DE VARIAS VARIABLES J. Gómez-García
Aplicando las leyes de Morgan a la suma de minterms y al
producto de maxterms.
F = (A + B + C)(A + B + C)(A + B + C)(A + B + C) =
F = ABC + A BC + A BC + ABC =
= ( A + B + C ) + ( A + B + C ) + ( A + B + C) + ( A + B + C )
= (ABC)·(A BC)·(A BC)·(ABC)

11. CIRCUITOS DIGITALES – FUNCIONES LÓGICAS DE VARIAS VARIABLES J. Gómez-García
Aplicando las leyes de Morgan al producto de maxterms, dentro
de éstos, se obtiene la forma “AND-OR INVERTIDA” (AOI)
F = (A + B + C)(A + B + C)(A + B + C)(A + B + C) =
= ( A + B + C) + ( A + B + C ) + ( A + B + C ) + ( A + B + C ) =
= A BC + A BC + ABC + ABC

12. CIRCUITOS DIGITALES – FUNCIONES LÓGICAS DE VARIAS VARIABLES J. Gómez-García
RESUMEN:
Toda función lógica se puede realizar mediante estructuras de
puertas de dos niveles:
•AND – OR
•OR – AND
•NAND – NAND
•NOR – NOR
•AOI
Destacando las puertas NAND y NOR que son conjuntos
autosuficientes.