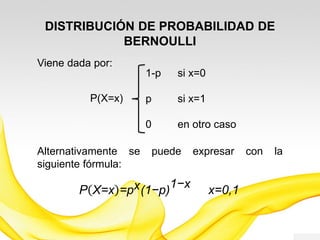
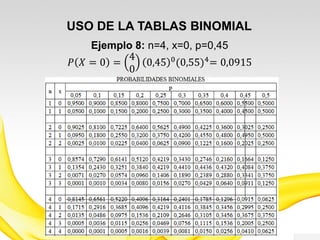
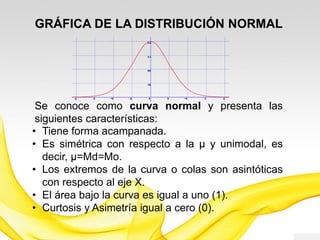
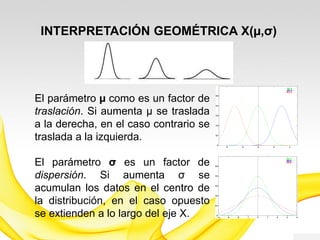
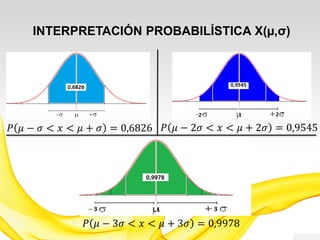
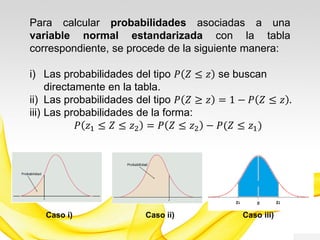
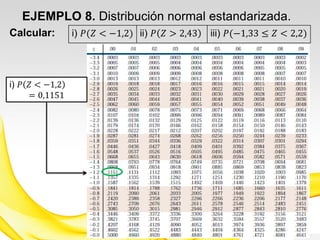
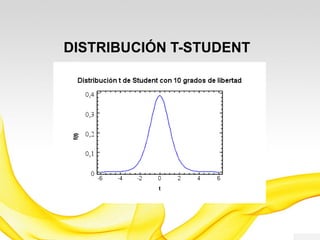
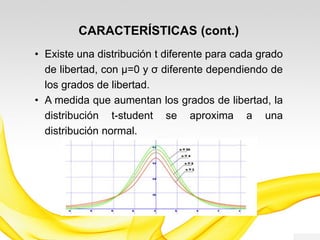
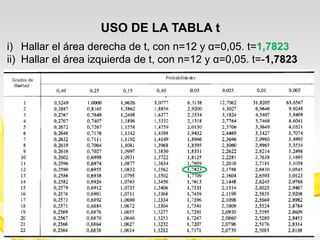
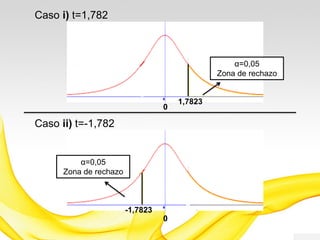
Este documento presenta una introducción a los modelos de probabilidad y distribuciones de probabilidad, incluyendo distribuciones discretas como la de Bernoulli y binomial, y distribuciones continuas como la normal. Explica conceptos clave como experimentos aleatorios, variables aleatorias, parámetros de distribución, y cómo los modelos de probabilidad permiten representar fenómenos reales de manera simplificada mediante afirmaciones probabilísticas. También incluye ejemplos para ilustrar diferentes tipos de experimentos y distribuciones.