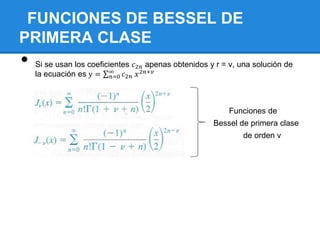
Este documento describe las ecuaciones de Bessel, sus aplicaciones (propagación de ondas, potenciales estáticos, etc.), y cómo resolverlas. Presenta las funciones de Bessel de primera y segunda clase, y explica que la solución general de la ecuación de Bessel depende de si el orden v es un entero o no. También cubre ecuaciones relacionadas como la paramétrica y modificada de Bessel, y cómo ciertas ecuaciones diferenciales pueden expresarse en términos de Bessel.

1. ECUACIÓN DE
BESSEL
Juan Camilo Sacanamboy

2. APLICACIONES
• Propagación de ondas.
• Potenciales estáticos.
• Conducción del calor en objetos cilíndricos.
• Difusión de una red.
• Procesamiento de señales.

3. INTRODUCCIÓN
• Ecuación de Bessel de orden v
• Cuando se resuelve la ecuación se supone
que 𝑣 ≥ 0

4. SOLUCIÓN
x=0 es un punto no singular regular de la ecuación de Bessel, se sabe que
existe al menos una solución de la forma y = ∞ 𝑐 𝑛 𝑥 𝑛+𝑟 (T. Frobenius)
𝑛=0
• Ecuación indicial: 𝑟 2 − 𝑣 2 = 0
o Raíces indiciales: 𝑟1 = 𝑣 y 𝑟2 = −𝑣

5. SOLUCIÓN
• 𝑟1 = v
Entonces,

6. SOLUCIÓN
• La elección c1 = 0 implica que c3=c5=c7=...=0, por lo que para k=0,2,4,...
se encuentra, después de establecer k+2=2n, n=1,2,3,..., que
• Con esto se tiene que,

7. SOLUCIÓN
En la práctica se acostumbra a elegir a 𝑐0 como
Reescribiendo,

8. FUNCIONES DE BESSEL DE
PRIMERA CLASE
• Si se usan los coeficientes 𝑐2𝑛 apenas obtenidos y r = v, una solución de
la ecuación es y = ∞ 𝑐2𝑛 𝑥 2𝑛+𝑣
𝑛=0
Funciones de
Bessel de primera clase
de orden v

9. SOLUCIÓN GENERAL
• v = 0 : ambas soluciones son la misma (Problema!)
• v > 0 y 𝑟1 − 𝑟2 = 𝑣 − −𝑣 = 2𝑣 no es un entero positivo
o Caso I-Sección 6.2: 𝐽 𝑣 𝑥 y 𝐽−𝑣 𝑥 son li
 𝑦 = 𝑐1 𝐽 𝑣 𝑥 + 𝑐2 𝐽−𝑣 𝑥 . (Bien!)
• v > 0 y 𝑟1 − 𝑟2 = 𝑣 − −𝑣 = 2𝑣 es un entero positivo
o Dos posibilidades
 v=m=entero positivo: 𝐽−𝑚 (𝑥)y 𝐽 𝑚 (𝑥) no son li (Propiedad (i) )
(Problema!)
 v es la mitad de un entero positivo impar: 𝐽−𝑣 (𝑥)y 𝐽 𝑣 (𝑥) son li (Bien!)
• La solución general en (0, ∞) es
 𝒚 = 𝒄 𝟏 𝑱 𝒗 𝒙 + 𝒄 𝟐 𝑱−𝒗 (𝒙), 𝒗 ≠ 𝒆𝒏𝒕𝒆𝒓𝒐.

10. ECUACIÓN DE BESSEL DE
SEGUNDA CLASE
• Para cualquier valor de v la solución general
en 0, ∞ se puede escribir como:
• 𝒚 = 𝒄 𝟏 𝑱 𝒗 𝒙 + 𝒄 𝟐 𝒀 𝒗 (𝒙), donde
𝑐𝑜𝑠𝑣𝜋 𝐽 𝑣 𝑥 −𝐽−𝑣 (𝑥)
𝑌𝑣 𝑥 =
𝑠𝑒𝑛𝑣𝜋
Función de Bessel de segunda clase de orden v

11. ED RESOLUBLES EN TÉRMINOS
DE BESSEL
• Algunas veces es posible convertir a una ED
de Bessel con un cambio de variable
o 𝒙 𝟐 𝒚′′ + 𝒙𝒚′ + ∝ 𝟐 𝒙 𝟐 − 𝒗 𝟐 𝒚 = 𝟎 : Ecuación
paramétrica de Bessel de orden v
o 𝒙 𝟐 𝒚′′ + 𝒙𝒚′ + 𝒙 𝟐 + 𝒗 𝟐 𝒚 = 𝟎 : Ecuación modificada
de Bessel de orden v
𝟏−𝟐𝒂 𝒂 𝟐 −𝒑 𝟐 𝒄 𝟐
o 𝒚′′ + 𝒚′ + 𝒃𝟐 𝒄𝟐 𝒙 𝟐𝒄−𝟐 + 𝒚 = 𝟎, 𝒑 ≥ 𝟎:
𝒙 𝒙𝟐
Ecuación especial

12. ECUACIÓN PARAMÉTRICA DE
BESSEL DE ORDEN V
• Problemas con valores en la frontera relacionados con ED parciales
(coordenadas cilíndricas)
𝒙 𝟐 𝒚′′ + 𝒙𝒚′ + ∝ 𝟐 𝒙 𝟐 − 𝒗 𝟐 𝒚 = 𝟎
𝑡 =∝ 𝑥, ∝> 0
Forma Bessel
Solución:

13. ECUACIÓN MODIFICADA DE
BESSEL DE ORDEN V
• 𝒙 𝟐 𝒚′′ + 𝒙𝒚′ + 𝒙 𝟐 + 𝒗 𝟐 𝒚 = 𝟎
𝑡 = 𝑖𝑥 , 𝑖 2 = −1
Reemplazando,
Forma de Bessel
Solución para todo v
Donde, 𝐼𝑣 𝑥 𝑦 𝐾𝑣 𝑥 𝑠𝑜𝑛 𝑙𝑖

14. ECUACIÓN ESPECIAL
• 𝒚′′ +
𝟏−𝟐𝒂
𝒙
𝒚′ + 𝒃 𝟐 𝒄 𝟐 𝒙 𝟐𝒄−𝟐 +
𝒂 𝟐 −𝒑 𝟐 𝒄 𝟐
𝒙𝟐
𝒚 = 𝟎,
𝒑 ≥ 𝟎:
Muchas ED se ajustan a su forma mediante
elecciones apropiadas de los parámetros
Solución: 𝒚 = 𝒙 𝒂 [𝒄 𝟏 𝑱 𝒑 𝒃𝒙 𝒄 + 𝒄 𝟐 𝒀 𝒑 (𝒃𝒙 𝒄 )

15. TABLA
• Bessel General:
• Bessel Paramétrica
 , 𝑡 =∝ 𝑥 ∝≥ 0
• Bessel modificada: