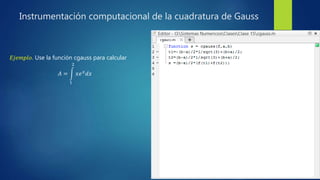
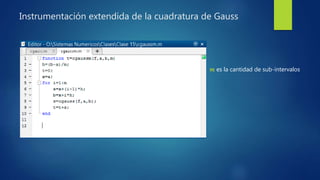
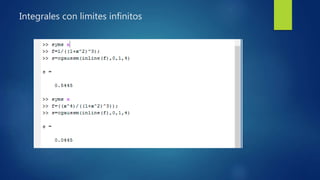
Este documento describe el método de los coeficientes indeterminados para obtener fórmulas de integración numérica. Se usa este método para derivar la fórmula de Simpson de tres puntos y la fórmula de Gauss para dos puntos, las cuales son exactas para polinomios de cierto grado. Se resuelven sistemas de ecuaciones no lineales para determinar los coeficientes y puntos de integración en cada caso.

1. Cuadratura de Gauss
CLASE 14
23-JULIO-2014

2. Obtención de fórmulas de integración numérica con el
método de coeficientes indeterminados
 Describiremos una técnica denominada de los Coeficientes
indeterminados para obtener fórmulas de integración numérica.
 El procedimiento consiste en proponer una fórmula conteniendo algunas
incógnitas. Esta formula es aplicada a casos conocidos con el propósito de
obtener ecuaciones, de las cuales se determinan los valores para las
incógnitas.

3. Obtención de fórmulas de integración numérica con el
método de coeficientes indeterminados
 Describiremos una técnica denominada de los Coeficientes
indeterminados para obtener fórmulas de integración numérica.
 Como ejemplo se usa este método para obtener una fórmula de tres
puntos espaciados en h:
𝑓 0 𝑓 ℎ 𝑓 2ℎ
0 ℎ 2ℎ

4. Obtención de fórmulas de integración numérica con el
método de coeficientes indeterminados
 Formula propuesta
 𝐴 = 0
2ℎ
𝑓 𝑥 𝑑𝑥 = 𝑐0 𝑓 0 + 𝑐1 𝑓 ℎ + 𝑐2 𝑓(2ℎ)
 Deben determinarse los coeficientes 𝑐0, 𝑐1, 𝑐2. Para obtenerlos, se usaran
tres casos con polinomios de grado 0, 1 y 2 con los cuales que se cumpla
la formula. Es suficiente considerar la forma mas simple del caso:

5. Obtención de fórmulas de integración numérica con el
método de coeficientes indeterminados
1. 𝑓 𝑥 = 1,
𝐴 =
0
2ℎ
1 𝑑𝑥 = 2ℎ = 𝑐0 𝑓 0 + 𝑐1 𝑓 ℎ + 𝑐2 𝑓 2ℎ = 𝑐0 1 + 𝑐1 1 + 𝑐2 1 ⟹ 𝑐0 + 𝑐1 + 𝑐2 = 2ℎ
2. 𝑓 𝑥 = 𝑥,
𝐴 =
0
2ℎ
𝑥𝑑𝑥 = 2ℎ2
= 𝑐0 𝑓 0 + 𝑐1 𝑓 ℎ + 𝑐2 𝑓 2ℎ = 𝑐0 0 + 𝑐1 ℎ + 𝑐2 2ℎ ⟹ 𝑐1 + 2𝑐2 = 2ℎ

6. Obtención de fórmulas de integración numérica con el
método de coeficientes indeterminados
3. 𝑓 𝑥 = 𝑥2
,
𝐴 =
0
2ℎ
𝑥2
𝑑𝑥 =
8ℎ3
3
= 𝑐0 𝑓 0 + 𝑐1 𝑓 ℎ + 𝑐2 𝑓 2ℎ = 𝑐0 0 + 𝑐1 ℎ2
+ 𝑐2 4ℎ2
⟹ 𝑐1 + 4𝑐2 =
8
3
ℎ
Resolviendo las tres ecuaciones resultantes se obtienen:
𝒄 𝟎 =
𝒉
𝟑
, 𝒄 𝟏 =
𝟒𝒉
𝟑
, 𝒄 𝟐 =
𝒉
𝟑

7. Obtención de fórmulas de integración numérica con el
método de coeficientes indeterminados
 Reemplazando en la formula propuesta se llega a la conocida formula de Simpson
 𝑨 =
𝒉
𝟑
𝒇 𝟎 + 𝟒𝒇 𝒉 + 𝒇(𝟐𝒉)
 La obtención de la implica que es exacta si 𝑓 es un polinomio de grado menor o igual a dos.
Para otra 𝑓, será una aproximación equivalente a sustituir 𝑓 por un polinomio de grado dos.

8. Cuadratura de Gauss
 La formulas de Newton-Cotes estudiadas utilizan polinomios de
interpolación construidos con puntos fijos equidistantes. Estas formulas
son exactas si la función es un polinomio de grado menor o igual al
polinomio de interpolación respectivo.
 Si se elimina la restricción de que los puntos sean fijos y equidistantes,
entonces las formulas de integración contendrán incógnitas adicionales.

9. Cuadratura de Gauss
 La cuadratura de Gauss propone una formula general en la que los puntos
incluidos no son fijos como en las formulas de Newton-Cotes:
 𝑨 = 𝒂
𝒃
𝒇 𝒙 𝒅𝒙 = 𝒄 𝒐 𝒇 𝒕 𝟎 + 𝒄 𝟏 𝒇 𝒕 𝟏 + ⋯ + 𝒄 𝒎 𝒇 𝒕 𝒎
 Los puntos 𝑡0, 𝑡1, … , 𝑡 𝑚 son desconocidos. Adicionalmente también deben
determinarse los coeficientes 𝑐0, 𝑐1, … , 𝑐 𝑚
 El caso simple es la formula de dos puntos. Se usa el método de los
coeficientes indeterminados para determinar la cuatro incognitas.

10. Fórmula de la Cuadratura de Gauss con dos puntos
 Formula propuesta
 𝐴 = 𝑎
𝑏
𝑓 𝑥 𝑑𝑥 = 𝑐0 𝑓 𝑡0 + 𝑐1 𝑓(𝑡1)
 Por simplicidad se usará el intervalo −1, 1 para integrar. Mediante una
sustitución al caso general:
 𝐴 = −1
1
𝑓 𝑡 𝑑𝑡 = 𝑐 𝑜 𝑓 𝑡0 + 𝑐1 𝑓(𝑡1)
 Habiendo cuatro incógnitas se tomarán cuatro casos en los que la fórmula sea
exacta. Se usarán polinomios de grado 0, 1 , 2 𝑦 3. Es suficiente considerarlos en
su forma más simple:

11. Fórmula de la Cuadratura de Gauss con dos puntos
1. 𝑓 𝑡 = 1, 𝐴 = −1
1
1 𝑑𝑡 = 2 = 𝑐0 𝑓 𝑡0 + 𝑐1 𝑓 𝑡1 = 𝑐0 1 + 𝑐1 1 ⟹ 2 = 𝑐0 + 𝑐1
2. 𝑓 𝑡 = 𝑡, 𝐴 = −1
1
𝑡𝑑𝑡 = 0 = 𝑐0 𝑓 𝑡0 + 𝑐1 𝑓 𝑡1 = 𝑐0 𝑡0 + 𝑐1 𝑡1 ⟹ 0 = 𝑐0 𝑡0 + 𝑐1 𝑡1
3. 𝑓 𝑡 = 𝑡2
, 𝐴 = −1
1
𝑡2
𝑑𝑡 =
2
3
= 𝑐0 𝑓 𝑡0 + 𝑐1 𝑓 𝑡1 = 𝑐0 𝑡0
2
+ 𝑐1 𝑡1
2
⟹
2
3
= 𝑐0 𝑡0
2
+ 𝑐1 𝑡1
2
4. 𝑓 𝑡 = 𝑡3
, 𝐴 = −1
1
𝑡3
𝑑𝑡 = 0 = 𝑐0 𝑓 𝑡0 + 𝑐1 𝑓 𝑡1 = 𝑐0 𝑡0
3
+ 𝑐1 𝑡1
3
⟹ 0 = 𝑐0 𝑡0
3
+ 𝑐1 𝑡1
3

12. Fórmula de la Cuadratura de Gauss con dos puntos
 Se genera un sistema de cuatro ecuaciones no lineales. Una solución para
este sistema se obtiene con facilidad mediante una simple sustitución:
 Los valores 𝑐0 = 𝑐1 = 1 satisface a la ecuación (1)
 De la ecuación (2) se tiene 𝑡0 = −𝑡1. Esto satisface también a la ecuación
(4)

13. Fórmula de la Cuadratura de Gauss con dos puntos
 Finalmente sustituyendo 𝑡0 = −𝑡1 en la ecuación (3):

2
3
= 1 −𝑡1
2 + (1) 𝑡1
2 se obtiene:
 𝑡1 =
1
3
, entonces, 𝑡0 = −
1
3
y se reemplazan en la formula propuesta.

14. Fórmula de la Cuadratura de Gauss con dos puntos
 Definición: Fórmula de cuadratura de Gauss con dos puntos
 𝐴 = −1
1
𝑓 𝑡 𝑑𝑡 = 𝑐0 𝑓 𝑡0 + 𝑐1 𝑓 𝑡1 = 𝑓 −
1
3
+ 𝑓
1
3
 Esta simple fórmula es exacta si 𝑓 es un polinomio de grado menor o igual
a tres. Para otra 𝑓 es una aproximación equivalente a sustituir 𝑓 con un
polinomio de grado tres.

15. Fórmula de la Cuadratura de Gauss con dos puntos
 Ejemplo. Calcule 𝐴 = −1
1
2𝑡3
+ 𝑡2
− 1 𝑑𝑡
 𝐴 = −1
1
𝑓 𝑡 𝑑𝑡 = 𝑓 −
1
3
+ 𝑓
1
3
=
 2 −
1
3
3
+ −
1
3
3
− 1 + 2
1
3
3
+
1
3
3
− 1 = −
4
3
 La respuesta es exacta pues 𝑓 es un polinomio de grado 3.

16. Fórmula de la Cuadratura de Gauss con dos puntos
 Mediante un cambio de variable se extiende la fórmula al caso general:
 𝐴 = 𝑎
𝑏
𝑓 𝑡 𝑑𝑡 = 𝑐0 𝑓 𝑡0 + 𝑐1 𝑓 𝑡1
 Sea 𝑥 =
𝑏−𝑎
2
𝑡 +
𝑏+𝑎
2
 Se tiene que 𝑡 = 1 ⟹ 𝑥 = 𝑏, 𝑡 = −1 ⟹ 𝑥 = 𝑎, 𝑑𝑥 =
𝑏−𝑎
2
𝑑𝑡
 Sustituyendo se tiene

17. Fórmula de la Cuadratura de Gauss con dos puntos
 Definición: Formula de Cuadratura de Gauss para dos puntos
 𝐴 = 𝑎
𝑏
𝑓 𝑥 𝑑𝑥 =
𝑏−𝑎
2 −1
1
𝑓
𝑏−𝑎
2
𝑡 +
𝑏+𝑎
2
𝑑𝑡 =
𝑏−𝑎
2
𝑓 −
1
3
+ 𝑓
1
3
 Esta simple fórmula es exacta si 𝑓 es un polinomio de grado menor o igual
a tres. Para otra 𝑓 es una aproximación equivalente a sustituir 𝑓 con un
polinomio de grado tres.

18. Fórmula de la Cuadratura de Gauss con dos puntos
 Ejemplo
 Calcule 𝐴 = −1
1
2𝑡3 + 𝑡2 − 1 𝑑𝑡

19. Fórmula de la Cuadratura de Gauss con dos puntos
 Solución Analítica
 𝐴 = −1
1
𝑓 𝑡 𝑑𝑡 = 𝑓 −
1
3
+ 𝑓
1
3
⟹
 = 2 −
1
3
2
+ −
1
3
2
− 1 + 2
1
3
2
+
1
3
2
− 1 = −
4
3
 La respuesta es exacta pues 𝑓 es un polinomio de grado 3.

20. Fórmula de la Cuadratura de Gauss con dos puntos
 Mediante un cambio de variable se extiende la formula al caso general:
 𝐴 = 𝑎
𝑏
𝑓 𝑥 𝑑𝑥 = 𝑐0 𝑓 𝑡0 + 𝑐1 𝑓 𝑡1
 Sea 𝑥 =
𝑏−𝑎
2
𝑡 +
𝑏+𝑎
2
 Se tiene que 𝑡 = 1 ⟹ 𝑥 = 𝑏, 𝑡 = −1 ⟹ 𝑥 = 𝑎, 𝑑𝑥 =
𝑏−𝑎
2
𝑑𝑡
 Sustituyendo se tiene

21. Fórmula de la Cuadratura de Gauss con dos puntos
 Definición: Fórmula general de Cuadratura de Gauss para dos puntos:
 𝐴 = 𝑎
𝑏
𝑓 𝑥 𝑑𝑥 =
𝑏−𝑎
2 −1
1
𝑓
𝑏−𝑎
2
𝑡 +
𝑏+𝑎
2
𝑑𝑡 =
𝑏−𝑎
2
𝑓 −
1
3
+ 𝑓
1
3

22. Fórmula de la Cuadratura de Gauss con dos puntos
 Ejemplo: Calcule 𝐴 = 1
2
𝑥𝑒 𝑥
𝑑𝑥 con la fórmula de la cuadratura de Gauss
con dos puntos

23. Fórmula de la Cuadratura de Gauss con dos puntos
 Solución Analítica
 𝑥 =
𝑏−𝑎
2
𝑡 +
𝑏+𝑎
2
=
2−1
2
𝑡 +
2+1
2
=
1
2
𝑡 +
3
2
 𝐴 = 𝑎
𝑏
𝑓 𝑥 𝑑𝑥 =
𝑏−𝑎
2 −1
1
𝑓
𝑏−𝑎
2
𝑡 +
𝑏+𝑎
2
𝑑𝑡
 =
1
2 −1
1
𝑓
1
2
𝑡 +
3
2
𝑑𝑡 =
1
2 −1
1 1
2
𝑡 +
3
2
𝑒
1
2
𝑡+
3
2 𝑑𝑡
 =
1
2
𝑓 −
1
3
+ 𝑓
1
3

24. Fórmula de la Cuadratura de Gauss con dos puntos
 Solución Analítica
 =
1
2
−
1
2 3
+
3
2
𝑒
−
1
2 3
+
3
2 +
1
2 3
+
3
2
𝑒
1
2 3
+
3
2 = 7.3832
 La respuesta exacta con seis decimales es 7.389056

25. Instrumentación computacional de la cuadratura de Gauss
𝐸𝑗𝑒𝑚𝑝𝑙𝑜. Use la función cgauss para calcular
𝐴 =
1
2
𝑥𝑒 𝑥
𝑑𝑥

26. Instrumentación computacional de la cuadratura de Gauss

27. Instrumentación computacional de la cuadratura de Gauss
 Para mejorar la precisión de esta formula se le puede aplicar mas de una
vez dividiendo el intervalo de integración en sub-intervalos

28. Instrumentación computacional de la cuadratura de Gauss
 Ejemplo. Aplique dos veces la cuadratura de Gauss en el ejemplo anterior
 𝐴 = 1
2
𝑥𝑒 𝑥 𝑑𝑥 = 𝐴1 + 𝐴2 = 1
1.5
𝑥𝑒 𝑥 𝑑𝑥 + 1.5
2
𝑥𝑒 𝑥 𝑑𝑥
 Posteriormente corremos la función gauss en Matlab y aparecerá lo
siguiente

29. Instrumentación computacional de la cuadratura de Gauss

30. Instrumentación computacional de la cuadratura de Gauss
 Se puede dividir el intervalo en mas sub-intervalos para obtener mayor
precisión. Conviene definir una función en MATLAB para determinar la
precisión del resultado, comparando valores consecutivos, en base a la
convergencia de la integral.

31. Instrumentación extendida de la cuadratura de Gauss
𝑚 es la cantidad de sub-intervalos

32. Instrumentación extendida de la cuadratura de Gauss
 Ejemplo. Aplicar sucesivamente la Cuadratura de Gauss incrementando el
número de sub-intervalos hasta que la respuesta tenga cuatro decimales.

33. Instrumentación extendida de la cuadratura de Gauss

34. Instrumentación extendida de la cuadratura de Gauss
 En el ultimo se han usado 4 sub-intervalos. El valor obtenido tiene cuatro
decimales fijos.
 Para obtener formulas de cuadratura de Gauss con mas puntos no es
practico usar el método de coeficientes indeterminados. Se puede usar un
procedimiento general basado en la teoría de polinomios ortogonales.

35. Integrales con limites infinitos
 Estas integrales se denominan integrales impropias del primer tipo.
 Ocasionalmente pueden ser de interés calcular integrales cuyos limites no
se pueden evaluar en las formulas. Mediante alguna sustitución deben
reducirse a una forma simple eliminando estos limites impropios.

36. Integrales con limites infinitos
 Ejemplo. Calcule 𝐴 = 0
∞ 𝑑𝑥
1+𝑥2 3 con la cuadratura de Gauss
 𝑚 = 1,2,4

37. Integrales con limites infinitos
 Solución
 Antes de la sustitución conviene separar la integral en dos sub-intervalos
 𝐴 = 0
∞ 𝑑𝑥
1+𝑥2 3 = 0
1 𝑑𝑥
1+𝑥2 3 + 1
∞ 𝑑𝑥
1+𝑥2 3 = 𝐴1 + 𝐴2
 𝐴1 se puede calcular inmediatamente con la cuadratura de Gauss
 Para 𝐴2 se hace la sustitución
 𝑥 = 1/𝑡

38. Integrales con limites infinitos
 Solución
 𝑥 → ∞ ⟹ 𝑡 ⟶ 0, 𝑥 = 1 ⟹ 𝑡 = 1, 𝑑𝑥 = −1/𝑡2 𝑑𝑡
 𝐴 = 0
∞ 𝑑𝑥
1+𝑥2 3 = 1
0 1
1+1/𝑡2 3 −
𝑑𝑡
𝑡2 = 0
1 𝑡4
1+𝑡2 3 𝑑𝑡
 Ahora se puede aplicar la cuadratura de Gauss

39. Integrales con limites infinitos

40. Integrales con limites infinitos

41. Integrales con limites infinitos
 Resultados calculados:
 𝑚 = 1; 𝐴 = 𝐴1 + 𝐴2 = 0.6019
 𝑚 = 2; 𝐴 = 𝐴1 + 𝐴2 = 0.5891
 𝑚 = 4; 𝐴 = 𝐴1 + 𝐴2 = 0.5890
 El ultimo resultado tiene un error en el orden de 0.0001

42. Integrales con limites infinitos