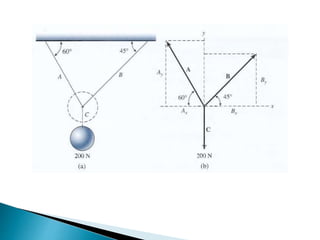
Una pelota de 200 N cuelga de una cuerda unida a otras dos cuerdas. Se aplica el equilibrio de fuerzas para encontrar las tensiones desconocidas en las cuerdas A, B y C. Se construye un diagrama de cuerpo libre y se escriben ecuaciones para las fuerzas a lo largo de los ejes x y y. Se resuelven las ecuaciones simultáneamente para encontrar que la tensión en A es 147 N, en B es 104 N, y en C es 200 N, igual al peso de la pelota.

1. Módulo: Interpretación de fenómenos
físicos de la materia
Docente: Pablo Prieto Gutiérrez
Semestre 11415

2.  Una pelota de 200 N cuelga de una cuerda
unida a otras dos cuerdas, como se observa
en la figura 4.10. Encuentre las tensiones en
las cuerdas A, B y C.

3.  Primero trazaremos un diagrama de cuerpo
libre y luego aplicaremos la primera
condición de equilibrio a fin de hallar las
tensiones desconocidas de las cuerdas.

4. Con base en el bosquejo proporcionado se construye
el diagrama de cuerpo libre (figura 4.10b). Las
componentes x y y, calculadas a partir de la figura,
se presentan en la tabla 4.2.
Al sumar las fuerzas a lo largo del eje x se obtiene:

7. 5 . Finalmente, se resuelve para las fuerzas
desconocidas. A partir de la ecuación (4.4) y como
sen 60° = 0.866, entonces
0.866A = 100 N

8. que puede simplificarse por sustitución de funciones
trigonométricas conocidas; o sea:
-0.5A + 0.7075 - 0

9. Se necesita más información para resolver esta
ecuación. Obtenemos una segunda ecuación
sumando las fuerzas a lo largo del eje y, lo que
resulta
0.866A + 0.707B = 200 N

10. Ahora se resuelven simultáneamente las ecuaciones
para A y B mediante el proceso de sustitución. Si se
despeja A de la ecuación se obtiene
Ahora se sustituye esta igualdad en la ecuación
(4.6) y se obtiene
0.866 (1.4145) + 0.7075 = 200 N

11. que se utiliza para despejar 5 como sigue:
Se puede calcular la tensión A sustituyendo 5 = 104 N
en la ecuación:
A = 1.4145 = 1.414(104 N) o A = 147 N
Desde luego, la tensión en la cuerda C es 200 N, ya
que debe ser igual al peso.

12. Bibliografía:
 Tippens, P. Física conceptos y aplicaciones;
Mc. Graw Hill, séptima edición
 http://conaeropago.blogspot.mx/
Docente: Pablo Prieto Gutiérrez