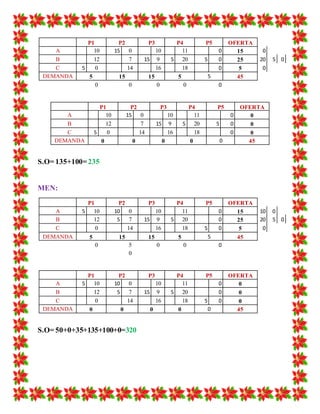
Este documento presenta dos ejercicios que involucran el método de asignación húngaro. El primero asigna cuatro vicepresidentes a inspeccionar cuatro plantas teniendo en cuenta su experiencia. El segundo asigna tres equipos de mantenimiento a realizar mantenimiento en tres máquinas. Ambos ejercicios utilizan matrices de asignación y reducción para encontrar la asignación óptima que minimice los costos totales.

1. EJERCICIOS DE ESQUINA DEL NOR-OESTRE
1.- La cervecería nacional tiene 3 plantas distribuidoras en la ciudad de Riobamba con ofertas de
500, 700, y 800 jabas respectivamente que deben ser distribuidas a 4 lugares cuyas demandas son
400, 900, 200, 500 jabas respectivamente.
¿Minimice el costo total del transporte si los costos unitarios se presentan en la siguiente tabla?
DISTRIBUIDORAS 1 2 3 4
OFERTA
A 12 13 4 6
500
B 6 4 10 11
700
C 10 9 12 4
800
DEMANDA 400 900 200 500 2000
DISTRIBUIDORAS 1 2 3 4 OFERTA
A 400 12 100 13 4 6 0
B 6 700 4 10 11 0
C 10 100 9 200 12 500 4 0
DEMANDA 0 0 0 0 2000
S.O: 4800+1300+2800+900+ 2400+ 2000=14200

2. EJERCICIOS MÉTODO DE DISTRIBUCIÓN MODIFICADA
(DIMO)
Ejercicio 1
1 2 3 4 OFERTA
1 12 13 4 6 500
2 6 4 10 11 700
3 10 9 12 4 800
DEMANDA 400 900 200 500 2000
Soluciónbásica factible obtenida aplicando el método de la Esquina Noroeste.
V
U
RUTA EN
USO
COSTO ECUACIÓN
11 12 U1+V1=12
12 13 U1+V2=13
22 4 U2+V2=4
32 9 U3+V2=9
33 12 U3+V3=12
34 4 U3+V4=4
1 2 3 4 OFERTA
1 400 12 100 13 4 6 500
2 6 700 4 10 11 700
3 10 100 9 200 12 500 4 800
DEMANDA 400 900 200 500 2000
LLENAS
U1=0
U2=-9
U3=-4
V1=12
V2=13
V3=16
V4=8
VACÍAS
e13=4-(0+16)=-12
e14=6-(0+8)=-2
e21=6-(-9+12)=3
e23=10-(-9+16)=3
e24=11-(-9+8)=12
e31=10-(-4+12)=2

3. NUEVA TABLA
V
U
NUEVA TABLA
ECUACIÓN
U1+V1=12
U1+V3=4
U2+V2=4
U3+V1=10
U3+V2=9
U3+V4=4
SO=12000
Ejercicio 2
C1 C2 C3 C4 OFERTA
D1 25 600 700 700 0 25
D2 5 320 35 300 350 0 40
D3 500 0 480 25 450 25 0 50
DEMANDA 30 35 25 25 115
1 2 3 4 OFERTA
1 400 12 13 100 4 6 500
2 6 700 4 10 11 700
3 10 200 9 100 12 500 4 800
DEMANDA 400 900 200 500 2000
LLENAS
U1=0
U2=3
U3=8
V1=12
V2=-1
V3=4
V4=-4
ECUACION
U1+V1=12
U1+V3=4
U2+V2=4
U3+V2=9
U3+V3=12
U3+V4=4
VACÍAS
e14=13-(0+1)=-12
e14=6-(0+4)=10
e21=6-(3+12)=9
e24=10-(1-4)=3
e24=11-(3+4)=12
e31=10-(8+12)=12
V
1 2 3 4 OFERTA
U
1 300 12 13 200 4 6 500
2 6 700 4 10 11 700
3 100 10 200 9 12 500 4 800
DEMANDA 400 900 200 500 2000
LLENAS
U1=12
U2=5
U3=10
V1=0
V2=-1
V3=-8
V4=-6
VACÍAS
e12=13-(12-1)=2
e14=6-(12-6)=0
e21=6-(5-0)=1
e23=10-(5-8)=13
e24=11-(5-6)=12
e31=12-(10-8)=10

4. S.O= 15000+1600+10500+11250+0=38.350
ECUACIÓN
U1+V1=600
U2+V1=320
U2+V2=35
U3+V2=480
U3+V3=450
U3+V4=0
NUEVA TABLA
C1 C2 C3 C4 OFERTA
D1 0 600 700 700 25 0 25
D2 30 320 10 300 350 0 40
D3 500 25 480 25 450 0 0 50
DEMANDA 30 35 25 25 115
SO=35.850
ECUACIÓN
U1+V1=600
U1+V4=0
U2+V1=320
U2+V2=300
U3+V2=480
U3+V3=450
U3+V4=0
LLENAS
U1=0
U2=-280
U3=-100
V1=600
V2=-580
V3=-550
V4=-100
VACÍAS
e12=13-(12-1)=2
e13=700-(0+550)=150
e14=0-(0+100)=-100
e23=350-(280+550)=80
e24=0-(-280+100)=180
e31=500-(-100+600)=0
LLENAS
U1=0
U2=-320
U3=-500
V1=600
V2=-20
V3=-50
V4=-500
VACÍAS
e12=700-(0-20)=720
e13=700-(0+50)=750
e23=350-(320+50)=-80
e24=0-(320+500)=180

5. EJERCICIOS MÉTODO DE APROXIMACIÓN DE VOGEL
(MAV)
Ejercicio 1
PLANTAS
PUERTOS 1 2 3 4 OFERTA
1 12 13 4 6 500
2 6 4 10 11 700
3 10 9 12 4 800
DEMANDA 400 900 200 500 2000
PLANTAS PENALI.
PUERTOS 1 2 3 4 OFERTA 2
1 12 13 200 4 6 300 2
2 6 4 10 11 700 5
3 10 9 12 4 800
DEMANDA 400 900 0 500 2000
PENALI. 4 5 6 2
PLANTAS
PUERTOS 1 2 3 4 OFERTA PENALI
1 12 13 200 4 300 6 0 6
2 6 4 10 11 700 2
3 10 9 12 4 800 5
DEMANDA 400 900 0 200 2000

6. PLANTAS
PUERTOS 1 2 3 4 OFERTA PENALI
1 12 13 200 4 300 6 0
2 6 4 10 11 700 2
3 10 9 12 200 4 600 6
DEMANDA 400 900 0 0 2000
PENALI 4 5 7
PLANTAS
PUERTOS 1 2 3 4 OFERTA PENALI
1 12 13 200 4 300 6 0
2 6 700 4 10 11 0 2
3 10 9 12 200 4 600 1
DEMANDA 400 200 0 0 2000
PENALI 4 5
PLANTAS
PUERTOS 1 2 3 4 OFERTA
1 12 13 200 4 300 6 0
2 6 700 4 10 11 0
3 400 10 200 9 12 200 4 0
DEMANDA 0 0 0 0 2000
F.O= 200(4)+300(6)+700(4)+400(10)+200(9)+200(4)= 12.000
Ejercicio 2
PLANTAS
PUERTOS 1 2 3 4 OFERTA
1 6 7 2 4 200
2 2 5 13 12 800
3 7 3 4 5 1400
DEMANDA 200 400 600 1200 2400

7. PLANTAS
PUERTOS 1 2 3 4 OFERTA PENALI
1 6 7 2 4 200 2
2 200 2 5 13 12 600 3
3 7 3 4 5 1400 1
DEMANDA 0 400 600 1200 2200
PENALI 4 2 2 1
PLANTAS
PUERTOS 1 2 3 4 OFERTA PENALI
1 6 7 2 4 200 2
2 200 2 400 5 13 12 200 7
3 7 3 4 5 1400 1
DEMANDA 0 0 600 1200 1800
PENALI 2 2 1
PLANTAS
PUERTOS 1 2 3 4 OFERTA PENALI
1 6 7 200 2 4 0 2
2 200 2 400 5 13 12 200 1
3 7 3 4 5 1400 1
DEMANDA 0 0 400 1200 1600
PENALI 2 1
PLANTAS
PUERTOS 1 2 3 4 OFERTA PENALI
1 6 7 200 2 4 0
2 200 2 400 5 13 12 200 1
3 7 3 400 4 5 1000 1
DEMANDA 0 0 0 1200 1200
PENALI 9 7

8. PLANTAS
PUERTOS 1 2 3 4 OFERTA
1 6 7 200 2 4 0
2 200 2 400 5 13 200 12 0
3 7 3 400 4 1000 5 0
DEMANDA 0 0 0 0 0
F.0= 200(2)+200(2)+400(5)+200(12)+400(4)+1000(5)=11.800
EJERCICIOS MÉTODO DE ASIGNACIÓN O HÚNGARO
Ejercicio 1
La gerencia general de RPG con sede en Bruselas, este ano, como parte de su auditoria anual,
decidió que cada uno de sus cuatro vicepresidentes visite e inspeccione cada una de sus plantas de
ensamblaje durante las primeras dos semanas de junio. Las plantas están ubicadas en Leipzig
(Alemania), Nancy (Francia), Lieja (Bélgica), y Tilburgo (Holanda).
Para decidir a qué vicepresidente enviar a una planta determinada se asignaran puntos (costos) a
cada uno de ellos de acuerdo a su experiencia.
MATRIZ DE ASIGNACIÓN
Leipzig Nancy Lieja Tilburgo
Finanzas (F)(1) 24 10 21 11
Mercadotecnia (M)(2) 14 22 10 15
Operaciones (O)(3) 15 17 20 19
Personal (P)(4) 11 19 14 13
REDUCCIÓN DE FILAS
Leipzig Nancy Lieja Tilburgo
Finanzas (F)(1) 14 0 11 1
Mercadotecnia (M)(2) 4 12 0 5
Operaciones (O)(3) 0 2 5 4
Personal (P)(4) 0 8 3 2
REDUCCIÓN COLUMNAS

9. Leipzig Nancy Lieja Tilburgo
Finanzas (F)(1) 14 0 11 0
Mercadotecnia (M)(2) 4 12 0 4
Operaciones (O)(3) 0 2 5 3
Personal (P)(4) 0 8 3 1
MATRIZ REDUCIDA
Leipzig Nancy Lieja Tilburgo
Finanzas (F)(1) 15 0 12 0
Mercadotecnia (M)(2) 4 11 0 3
Operaciones (O)(3) 0 1 5 2
Personal (P)(4) 0 7 3 0
ASIGNACIÓN
Leipzig Nancy Lieja Tilburgo
Finanzas (F)(1) 15 0 12 0
Mercadotecnia (M)(2) 4 11 0 3
Operaciones (O)(3) 0 1 5 2
Personal (P)(4) 0 7 3 0
10+10+15+13=48
Ejercicio 2
La compañía de manufactura “Jiménez y Asociados” desea realizar una jornada de
mantenimiento preventiva a sus tres máquinas principales A B y C. El tiempo que demando
realizar el mantenimiento de cada máquina es de 1 día teniendo en cuenta que la compañía
cuenta con tres proveedores de servicios de mantenimiento debe de asignarse un equipo de
mantenimiento a cada máquina para poder cambiar.
MATRIZ DE ASIGNACIÓN

10. Maquina
1
Maquina
2
Maquina
3
Eq. Mantenimiento 1 10 9 5
Eq. Mantenimiento 2 9 8 3
Eq. Mantenimiento 3 6 4 7
REDUCCIÓN COLUMNAS
Maquina
1
Maquina
2
Maquina
3
Eq. Mantenimiento 1 4 5 2
Eq. Mantenimiento 2 3 4 0
Eq. Mantenimiento 3 0 0 4
REDUCCIÓN FILAS
Maquina
1
Maquina
2
Maquina
3
Eq. Mantenimiento 1 2 3 0
Eq. Mantenimiento 2 3 4 0
Eq. Mantenimiento 3 0 0 4
MATRIZ REDUCIDA
Maquina
1
Maquina
2
Maquina
3
Eq. Mantenimiento 1 0 1 0
Eq. Mantenimiento 2 1 2 0
Eq. Mantenimiento 3 0 0 6
ASIGNACIÓN
Maquina
1
Maquina
2
Maquina
3
Eq. Mantenimiento 1 0 1 0
Eq. Mantenimiento 2 1 2 0

11. Eq. Mantenimiento 3 0 0 6
10+3+4= 17
Ejercicio 3
MATRIZ DE ASIGNACIÓN
M1 M2 M3 M4
E1 10 9 5 4
E2 9 8 3 6
E3 6 4 7 9
E4 0 0 0 0
REDUCCIÓN FILAS
M1 M2 M3 M4
E1 6 5 1 0
E2 6 5 0 3
E3 2 0 3 5
E4 0 0 0 0
4+3+4+0=11
Ejercicio 4
Ejercicio de maximización:
Una organización de recolección de café cuenta con tres equipos de siembra y cosecha del mismo
(equipo 1,2,3). Estos equipos de trabajo se encuentran entrenados para trabajar en condiciones
particulares del proceso, condiciones como lo son el tipo de suelo, las condiciones del clima y el
tipo de grano.
La organización cuenta con 4 terrenos disponibles para efectuar el proceso de siembra y cosecha
(terreno A.B.C.D), estos terrenos tienen condiciones particulares de suelo, clima, y tipo de grano.
Cada equipo cuenta con la capacidad de efectuar el proceso con solo uno de los terrenos
disponibles, salvo el equipo 2 que cuenta con una serie de herramientas tecnológicas que le
permiten realizar la siembra y cosecha del grano en dos de los terrenos disponibles. Se ha

12. contratado a un ingeniero industrial con el objetivo de realizar las asignaciones precisas que
maximicen la cantidad de sacos de café cosechados en total. El siguiente tabulado muestra la
capacidad (en cientos de sacos) de cosecha de café e cada uno de los equipos dependiendo de cada
uno de los terrenos.
MATRIZ DE ASIGNACIÓN
MAXIMIZACIÓN
A B C D
E1 2 8 3 3
E2 5 2 0 8
E3 5 2 0 8
E4 2 5 7 8
REDUCCIÓN FILAS
A B C D
E1 0 6 1 1
E2 5 2 0 8
E3 5 2 0 8
E4 0 3 5 6
REDUCCIÓN COLUMNAS
A B C D
E1 0 4 1 0
E2 5 0 0 7
E3 5 0 0 7
E4 0 1 5 5
A B C D
E1 13 7 12 12
E2 10 13 15 7
E3 10 13 15 7
E4 13 10 8 7
COSTO MAS
ALTO

13. 12+13+15+13=53

14. EJERCICIOS MÉTODO DE COSTO MÍNIMO
Ejercicio 1
PUERTOS 1 2 3 4 OFERTA
1 12 13 4 6 500
2 6 4 10 11 700
3 10 9 12 4 800
DEMANDA 400 900 200 500 2000
PUERTOS 1 2 3 4 OFERTA
1 300 12 13 200 4 6 500 300 0
2 6 700 4 10 11 700 0
3 100 10 200 9 12 500 4 800
DEMANDA 400 900 200 500 2000 300 100 0
300 200 0 0
0 0
PUERTOS 1 2 3 4 OFERTA
1 300 12 13 200 4 6 0
2 6 700 4 10 11 0
3 100 10 200 9 12 500 4 0
DEMANDA 0 0 0 0 2000
S.O= 3600+800+2800++1000+1300+200= 12000
Ejercicio 2
La empresa INFORMATECH, está desarrollando cuatro proyectos de redes, y busca los mejores
costos de envió para las cajas de red
MCM:

15. P1 P2 P3 P4 P5 OFERTA
A 10 15 0 10 11 0 15 0
B 12 7 15 9 5 20 5 0 25 20 5 0
C 5 0 14 16 18 0 5 0
DEMANDA 5 15 15 5 5 45
0 0 0 0 0
P1 P2 P3 P4 P5 OFERTA
A 10 15 0 10 11 0 0
B 12 7 15 9 5 20 5 0 0
C 5 0 14 16 18 0 0
DEMANDA 0 0 0 0 0 45
S.O= 135+100=235
MEN:
P1 P2 P3 P4 P5 OFERTA
A 5 10 10 0 10 11 0 15 10 0
B 12 5 7 15 9 5 20 0 25 20 5 0
C 0 14 16 18 5 0 5 0
DEMANDA 5 15 15 5 5 45
0 5 0 0 0
0
P1 P2 P3 P4 P5 OFERTA
A 5 10 10 0 10 11 0 0
B 12 5 7 15 9 5 20 0 0
C 0 14 16 18 5 0 0
DEMANDA 0 0 0 0 0 45
S.O= 50+0+35+135+100+0=320

16. EJERCICIOS MÉTODO DE PASOS SECUENCIALES
Ejercicio 1
1 2 3 4 OFERTA
1 12 13 4 6 500
2 6 4 10 11 700
3 10 9 12 4 800
DEMANDA 400 900 200 500 2000
Soluciónbásica factible obtenida aplicando el método de la Esquina Noroeste.
1 2 3 4 OFERTA
1 400 12 100 - 13 + 4 6 0
2 6 700 4 10 11 0
3 10 100 + 9 200 - 12 500 4 0
DEMANDA 0 0 0 0 2000
S.O= 400(12)+100(13)+700(4)+100(9)+200(12)+500(4)=14.200
Costos de las Trayectorias

17. +(4)-(13)+(9)-(12)= -12 +(6)-(13)+(9)-(4) = -2
+(6)-(4)+(13)-(12)= 3 +(10)-(4)+(9)-(12) = 3
+(11)-(4)+(9)-(4) = 12 +(10)-(9)+(13)-(12)= 2
NUEVA TABLA
1 2 3 4 OFERTA
1 400 12 + 13 -100 4 6 0
2 6 -700 4 + 10 11 0
3 10 - 200+ 9 +100- 12 500 4 0
DEMANDA 0 0 0 0 0
4800+400+2800+1800+1200+2000=13000