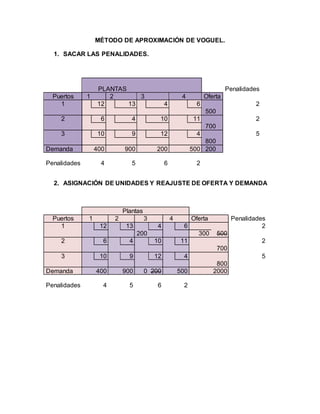
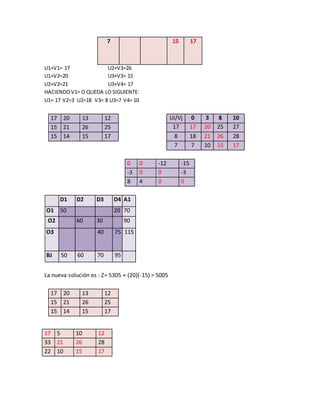
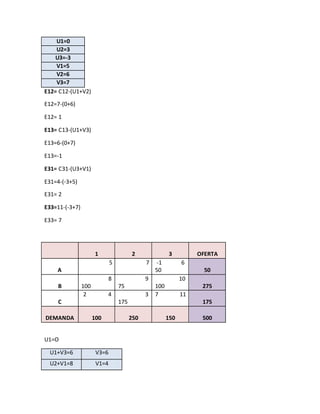
El documento describe varios métodos para resolver problemas de asignación y transporte, incluyendo el método de la esquina noroeste, el método del costo mínimo, el método de aproximación de Voguel y el método de pasos secuenciales. Estos métodos utilizan modelos matemáticos para asignar recursos de manera óptima minimizando costos sujeto a restricciones. El documento también incluye ejemplos numéricos ilustrativos de cada método.

1. INVESTIGACIÓN DE OPERACIONES.
La aplicación del Método científico para resolver problemas dando soluciones
óptimas.
1. El problema
2. Posibles soluciones.
3. Construir el modelo matemático.
4. Implantar el modelo matemático.
5. Validar el modelo matemático.
6. Solución (sino hay solución regresamos al segundo paso).
UN MODELO MATEMÁTICO.
1.- Función objetivo (maximizar, minimizar).
2.- Restricciones
3.- Limitaciones.
4.- Condiciones matemáticas.
EJEMPLOS:
1.- La cervecería Nacional tiene tres plantas distribuidoras en la Ciudad de
Riobamba con ofertas de 500, 700 y 800 javas respectivamente que deben ser
distribuidas a 4 lugares cuyas demandas son 400, 900, 200 y 500 javas
respectivamente. Minimice el costo total de transporte. Si los costos unitarios se
presentan en la siguiente tabla.
MÉTODO DE LA ESQUINA DEL NOROESTE
DISTRIBUIDO 1 2 3 4 OFERTA
12 13 4 6
1 400 100 500
6 4 10 11
2 700 700
10 9 12 4
3 100 200 500 800
DEMANDA 400 900 200 500 2000
SOLUCIÓN: 14200

2. METODO DEL COSTO MINIMO
Cantidad de unidades a una ruta disponible del costo mínimo.
EJEMPLOS:
1.- Dado:
A B C D OFERTA
D1
2 3 4 6
5 50 45 100
D2
1 5 8 3
120 120
8 5 1 4
D3 80 80
D4
4 5 6 3
5 90 95
DEMANDA 125 50 130 90 395
SOLUCIÓN
BASICA
FACTIBLE.
COSTO
MÍNIMO= 840

3. 2.- DADO:
MÉTODO DEL COSTO MÍNIMO
1 2 3 4 OFERTA
A
10 15 20 9
300 300
B
6 7 10 15
100 300 400
C
15 20 25 30
300 300 100 700
DEMANDA 100 600 300 400 1400
MÉTODO DE APROXIMACIÓN DE VOGUEL
Usa información de costos mediante el concepto de costo de oportunidad para
determinar una solución inicial factible.
Seleccionar en una fila la ruta más barata y la que le sigue. Hacer su diferencia
(penalidad que es el costo adicional por enviar una unidad desde el origen actual.
Lo anterior se repite para cada fila y cada columna esto es determinar todas las
penalidades.
Los pasos interactivos del Método de Voguel son los siguientes:
1. Identificar la fila o la columna con la máxima penalidad.
2. Colocar la máxima asignación posible a la ruta no usada que tenga menor
costo en la fila o la columna seleccionada en el punto uno (los empates se
resuelven arbitrariamente)
3. Reajustar la oferta y demanda en vista de esta asignación.
4. Eliminar la columna en la que haya quedado una demanda 0 (o la fila con
oferta 0), de consideraciones posteriores.
5. Calcular los nuevos costos de penalidad.

4. MÉTODO DE APROXIMACIÓN DE VOGUEL.
1. SACAR LAS PENALIDADES.
PLANTAS Penalidades
Puertos 1 2 3 4 Oferta
1 12 13 4 6 2
500
2 6 4 10 11 2
700
3 10 9 12 4 5
800
Demanda 400 900 200 500 200
Penalidades 4 5 6 2
2. ASIGNACIÓN DE UNIDADES Y REAJUSTE DE OFERTA Y DEMANDA
Plantas
Puertos 1 2 3 4 Oferta Penalidades
1 12 13 4 6 2
200 300 500
2 6 4 10 11 2
700
3 10 9 12 4 5
800
Demanda 400 900 0 200 500 2000
Penalidades 4 5 6 2

5. 3. ELIMINAR COLUMNA (FILA) CON DEMANDA (OFERTA) 0
Plantas
Puertos 1 2 3 4 Oferta Penalidades
1 12 13 4 6 2
200 300 500
2 6 4 10 11 2
700
3 10 9 12 4 5
800
Demanda 400 900 0 200 500 2000
Penalidades 4 5 6 2
4. CALCULAR LOS NUEVOS COSTOS DE PENALIDAD
Plantas
Puertos 1 2 3 4 Oferta Penalidades
1 12 13 4 6 6
200 300 500
2 6 4 10 11 2
700
3 10 9 12 4 5
800
Demanda 400 900 0 200 500 2000
Penalidades 4 5 2

6. 5. SOLUCIÓN BÁSICA FACTIBLE
Plantas
Puertos 1 2 3 4 Oferta Penalidades
1 12 13 4 6 6
200 300 300 500
2 6 4 10 11 2
700 0 700
3 10 9 12 4 5
400 200 200 600 800
Demanda 400 900 0 200 200 500 2000
Penalidades 4 5 2
Costo: 200*4+300*6+700*4+400*10+200*9+200*4 = $12.000
MÉTODO DE ASIGNACIÓN.
m= trabajadores
n=maquinas.
I= 1,2,3…m
J= 1,2,3…n
Cij
La gerencia general RPG (ejemplo de transportes con sede en Bruselas, este año
como parte de su Auditoria anual, decidió que cada uno de sus cuatro
Vicepresidentes visite e inspeccione cada una de sus plantas de ensamblaje
durante las primeras dos semanas de Junio. Las plantas están ubicadas en
Leipzig (Alemania), Nancy (Francia), Lieja en (Bélgica) y Tilburgo (Holanda).
Para decidir a qué vicepresidente enviar a una planta determinada, se asignaron
puntos (costos) a cada uno de ellos de acuerdo a su experiencia, habilidades
lingüísticas, tiempo que durara la inscripción y otros. Estos datos se muestran se
muestran en la siguiente tabla.

7. EJEMPLO:
Matriz de asignación:
Leipzig Nancy Liega Tilburgo
FINANZAS 24 10 21 11
MERCADOTECNIA 14 22 10 15
OPERACIONES 15 17 20 19
PERSONAL 11 19 14 13
Reducir en filas
1 2 3 4 pi
F 14 0 11 1 10
M 4 12 0 5 10
O 0 2 5 4 15
P 0 8 3 2 11
qj 1
Reducir
en
columnas
1 2 3 4 pi
F 14 0 11 0 10
M 4 12 0 4 10
O 0 2 5 3 15
P 0 8 3 1 11
qj 1

8. No es reducida: sólo tres rectas (para ser reducida deben ser 4)
1 2 3 4 pi
F 14 0
11
0 10
M 4 12 0 4 10
O 0 2 5 3 15
P 0 8 3 1 11
qj 1
1 2 3 4 pi
F 15 0 12 0 10
M 4 11 0 3 10
O 0 1 5 2 15
P 0 7 3 0 11
qj 1 + 1
1 2 3 4 pi
F 14 0 11 0 10
M 4 12 0 4 10
O 0 2 5 3 15
P 0 8 3 1 11
qj 1

9. 1 2 3 4 pi
F 15 0 12 0 10
M 4 11 0 3 10
O 0 1 5 2 15
P 0 7 3 0 11
qj 1 + 1
Costo = c12 + c23 + c31 +c44
= 10+10+15+13 = 48
MÉTODO DE PASOS SECUENCIALES
Una compañía tiene tres fábricas ubicadas en las sucursales A, B , C las cuales
proveen a los almacenes que están ubicados en D, E, F y G.
La capacidad de producción son de 70 y 90 y 115 unidades mensuales
respectivamente, mientras que las capacidades de los almacenes es de 50, 60, 70
y 95 unidades respectivamente.
El costo de envió de una unidad desde cada una de las fábricas a cada una de los
almacenes se presenta en el siguiente cuadro:
D1 D2 D3 D4
O1 17 20 13 12
02 15 21 26 25
03 15 14 15 17

10. D1 D2 D3 D4 OF
O1
17
50
20
20
13 12
70
02
15 21
40
26
50
25
90
O3 15 14 15
20
17
95 115
DEM 50 60 70 95
Z= 17*50+20*20+21*40+26*50+15+20+17*95 =5305
17 20
21 26
15 17
0 3 8 10
17 17 20
18 21 26

11. 7 15 17
U1+V1= 17 U2+V3=26
U1+V2=20 U3+V3= 15
U2+V2=21 U3+V4= 17
HACIENDOV1= O QUEDA LO SIGUIENTE:
U1= 17 V2=3 U2=18 V3= 8 U3=7 V4= 10
17 20 13 12
15 21 26 25
15 14 15 17
0 0 -12 -15
-3 0 0 -3
8 4 0 0
D1 D2 D3 D4 A1
O1 50 20 70
O2 60 30 90
O3 40 75 115
BJ 50 60 70 95
La nueva solución es : Z= 5305 + (20)(-15) = 5005
Ui/Vj 0 3 8 10
17 17 20 25 27
8 18 21 26 28
7 7 10 15 17
17 20 13 12
15 21 26 25
15 14 15 17
17 5 10 12
33 21 26 28
22 10 15 17

12. -
50
+
20
60 -
30
+
40
-
75
Nueva solución= Z= 5005+(30)(-18)= 4465
17 20 13 12
15 21 26 25
15 14 15 17
0 -6 -7 -5
17 17 23 10 12
15 15 21 8 10
22 22 28 15 17
70 70
0 15 3 0
-18 0 0 -3
-7 4 0 0
D1 D2 D3 D4 A1
O1 20 50 70
O2 30 60 90
O3 70 45 115
BJ 50 60 70 95
0 -3 3 0
0 0 18 15
-7 -14 0 0

13. 50 40 90
20 70 25 115
50 60 70 95
17 20 13 12
15 21 26 25
15 14 15 17
0 6 7 9
3 3 9 10 12
15 15 21 22 24
8 8 14 15 17
MÉTODO DE PASOS SECUENCIALES.
1.-
1 2 3 4 OFERTA
A
10 15 20 9
100 200 300
B
6 7 10 15
400 400
C
15 20 25 30
300 400 700
DEMANDA 100 600 300 400 1400
Respuesta: -6+7-15+10= -4
1 2 3 4 OFERTA
A
10 15 20 9
300 300
B
6 7 10 15
100 300 400
C 15 20 25 30
14 11 3 0
0 0 4 1
7 0 0 0

14. 300 400 700
DEMANDA 100 600 300 400 1400
Respuesta: -10+6-7+15= 4
Costo= 26.700
2.-
1 2 3 4 OFERTA
A
10 12 7 8
500 300 800
B
9 8 4 10
300 300
C
9 11 20 12
300 300 600
DEMANDA 500 600 300 300 1700
Respuestas: -9+8-12+10=-3
1 2 3 4 OFERTA
A
10 12 7 8
200 600 800
B
9 8 4 10
300 300
C
9 11 20 12
300 300 600
DEMANDA 500 600 300 300 1700
Respuesta:-8+12-10+9= 3
Costo= 21.500
3.-
1 2 3 4 OFERTA
A 22 20 17 18

15. 1200 600 1800
B
17 11 14 14
1600 700 2300
C
19 16 20 13
300 1300 1600
DEMANDA 1200 2200 1000 1300 5700
Respuestas:
-17+11-20+22= -4
-16+20-14+11= 1
-14+14-20+13= -7
1 2 3 4 OFERTA
A
22 20 17 18
1200 600 1800
B
17 11 14 14
1600 700 2300
C
19 16 20 13
1000 600 1600
DEMANDA 1200 2200 1000 1300 5700
Respuestas:
-17+11-20+22= -4
-14+20-13+14= 7
1 2 3 4 OFERTA
A
22 20 17 18
1800 1800
B
17 11 14 14
1200 400 700 2300
C
19 16 20 13
1000 600 1600

16. DEMANDA 1200 2200 1000 1300 5700
Respuesta:
-22+17-11+20= 4
Costo= 78.400
4.
1 2 3 OFERTA
1 80 80
2 20 140 160
3 10 180 190
DEMANDA 100 150 180 430
RESPUESTAS:
5-8+4-9=-8
6-9+8-7=-2
2-4+9-8=-1
1 2 3 OFERTA
1
-8
80 80
2 100 60 160
3 10 180 190
DEMANDA 100 150 180 430
RESPUESTAS:
8-5+9-4=8
58 1
4 9 6
2 8 7
58 1
4 9 6
2 8 7

17. 1-5+8-7=-3
6-9+8-7=-2
2-8+9-4=-1
1 2 3 OFERTA
1
-3
80 80
2 100 60 160
3 90 100 190
DEMANDA 100 150 180 430
5-1+7-8=3
6-9+8-7=-2
2-4+9-8=-1
1 2 3 OFERTA
1 80 80
2 100
-2
60 160
3 150 40 190
DEMANDA 100 150 180 430
5-1+7-8=3
9-6+7-8=2
2-7+6-4=-3
1 2 3 OFERTA
1 80 80
58 1
4 9 6
2 8 7
58 1
4 9 6
2 8 7
58 1

18. 2 60 100 160
3
-3
40 150 190
DEMANDA 100 150 180 430
RESPUESTAS:
8-1+6-4=9
9-4+2-8=-1
7-2+4-6=3
1 2 3 OFERTA
1 80 80
2
-1
60 100 160
3 100 90 190
DEMANDA 100 150 180 430
5-1+6-9=1
4-9+8-2=1
7-6+9-8=2
F.O= 80*1+60*9+100*6+100*2+90*8=2140
5.-
1 2 3 OFERTA
1 100 100
2 50 50 100
4 9 6
2 8 7
58 1
4 9 6
2 8 7
57 3
2 3 9

19. 3 100 100 200
DEMANDA 150 150 100 400
RESPUESTAS:
5-7+2-3=-3
9-3+4-1=9
5-2+3-4=2
1 2 3 OFERTA
1 50
-3
50 100
2 100 100
3 100 100 200
DEMANDA 150 150 100 400
RESPUESTAS:
3-5+4-1=1
3-5+7-2=3
5-4+5-7=-1
1 2 3 OFERTA
1 50 50 100
2 100 100
3
-1
100 100 200
DEMANDA 150 150 100 400
5 4 1
57 3
2 3 9
5 4 1
57 3
2 3 9
5 4 1

20. RESPUESTAS:
2-3+5-7=-3
3-7+5-1=0
4-5+7-5=1
1 2 3 OFERTA
1 100 100
2
-3
50 50 100
3 100 100 200
DEMANDA 150 150 100 400
RESPUESTAS:
7-5+3-2=3
9-2+5-1=11
4-3+2-5=-2
1 2 3 OFERTA
1 100 100
2 100 100
3 50
-2
50 100 200
DEMANDA 150 150 100 400
7-5+4-5=1
3-5+4-1=1
57 3
2 3 9
5 4 1
57 3
2 3 9
5 4 1

21. 3-2+5-4=2
9-2+5-1=11
F.O= 1250
MÉTODO DE DISTRIBUCIÓN MODIFICADA (MODI)
1.-
1 2 3 OFERTA
A
5
50
7
1
6
-8 50
B
8
50
9
225
10
-7 275
C
4
2
3
25
11
150 175
DEMANDA 100 250 150 500
RUTA EN USO COSTO ECUACIÓN
11
21
22
32
33
5
8
9
3
11
U1+V1=5
U2+V1=8
U2+V2=9
U3+V2=3
U3+V3=11
U=0
U1+V1=5 V1=5
U2+V1=8 U2=3
U2+V2=9 V2=6
U3+V2=3 U3=-3
U3+V3=11 V3=14
U1=0
U2=3
U3=-3

22. V1=5
V2=6
V3=14
E12= C12-(U1+V2)
E13= 7-(0+6)
E13= 1
E13= C13-(U1+V3)
E13= 6-(0+14)
E13= -8
E23= C23-(U2+V3)
E23= 10-(3+14)
E23=-7
E31= C31-(U3+V1)
E31= 4-(-3+5)
E31= 2
1 2 3 OFERTA
A
5
50
7 6
50
B
8
50
9
75
10
150 275
C
4 3
175
11
175
DEMANDA 100 250 150 500
U1=0
U1+V1=5 V1=5
U2+V1=8 U2=3
U2+V2=9 V2=6
U2+V3=10 V3=7
U3+V2=3 U3=-3

23. U1=0
U2=3
U3=-3
V1=5
V2=6
V3=7
E12= C12-(U1+V2)
E12=7-(0+6)
E12= 1
E13= C13-(U1+V3)
E13=6-(0+7)
E13=-1
E31= C31-(U3+V1)
E31=4-(-3+5)
E31= 2
E33=11-(-3+7)
E33= 7
1 2 3 OFERTA
A
5 7 -1 6
50 50
B
8
100
9
75
10
100 275
C
2 4 3
175
7 11
175
DEMANDA 100 250 150 500
U1=O
U1+V3=6 V3=6
U2+V1=8 V1=4

24. U1=0
U2=4
U3=-2
V1=4
V2=5
V3=6
E11= C11-(U1+V1)
E11=5-(0+4)
E11= 1
E12= C12-(U1+V2)
E12=7-(0+6)
E12= 1
E31= C31-(U3+V1)
E31=4-(-2+4)
E31= 2
E33= C33-(U3-V3)
E33=11-(-2+6)
E33= 7
1 2 3 OFERTA
A
5 1 7 -1 6
50 50
B
8
100
9
75
10
100 275
U2+V2=9 V2=5
U2+V3=10 U2=4
U3+V2=3 U3=-2

25. C
2 4 3
175
7 11
175
DEMANDA 100 250 150 500
V.O=3300
2.-
1 2 3 OFERTA
A
8
40
1 5 9
40
B
6
20
3
80
12
100
C
2 7
40
4
110 150
DEMANDA 60 120 110 290
RUTA EN USO COSTO ECUACIÓN
11
21
22
32
33
8
6
3
7
4
U1+V1=8
U2+V1=6
U2+V2=3
U3+V2=7
U3+V3=4
U1=0
U1+V1=8 V1=8
U2+V1=6 U2=-2
U2+V2=3 V2=5
U3+V2=7 U3=2
U3+V3=4 V3=2
U1=0
U2=-2
U3=2

26. V1=8
V2=5
V3=2
E12= C12-(U1+V2)
E12=5-(0+5)
E12=0
E13= C13-(U1+V3)
E13=9-(0+2)
E13= 7
E23= C23-(U2+V3)
E23=12-(-2+2)
E23= 12
E31= C31-(U3+V1)
E31=2-(2+8)
E31=-8
1 2 3 OFERTA
A
8
40
0 5 7 9
40
B
6 3
100
12 12
100
C
-8 2
20
7
20
4
110 150
DEMANDA 60 120 110 290
U1=0
U1+V1=8 V1=8
U2+V2=3 U2=-10
U3+V1=2 U3=-6

27. U3+V2=7 V2=13
U3+V3=4 V3=10
U1=0
U2=-10
U3=-6
V1=8
V2=13
V3=10
E12= C12-(U1+V2)
E12=5-(0+13)
E12= -8
E13= C13-(U1+V3)
E13=9-(0+10)
E13=-1
E21= C21-(U2+V1)
E21=6-(-10+8)
E21= 8
E23= C23-(U2+V3)
E23=12-(-10+10)
E23= 12
1 2 3 OFERTA
A
8
20
-8 5
20
-1 9
40
B
8 6 3
100
12 12
100
C
2
40
7 4
110 150
DEMANDA 60 120 110 290

28. U1=0
U1+V1=8 V1=8
U1+V2=5 V2=5
U2+V2=3 U2=-2
U3+V1=2 U3=-6
U3+V3=4 V3=10
U1=0
U2=-2
U3=-6
V1=8
V2=5
V3=10
E13= C13-(U1+V3)
E13=9-(0+10)
E13= -1
E21= C21-(U2+V1)
E21=6-(-2+8)
E21= 0
E23= C23-(U2-V1)
E23=12-(-2+8)
E23= 6
E32= C32-(U3-V2)
E32=7-(-6+5)
E32= 8

29. 1 2 3 OFERTA
A
8 5
20
-1 9
20 40
B
0 6 3
100
6 12
100
C
2
60
8 7 4
90 150
DEMANDA 60 120 110 290
U1=0
U1+V2=5 V2=5
U1+V3=9 V3=9
U2+V2=3 U2=-2
U3+V1=2 V1=7
U3+V3=4 U3=-5
U1=0
U2=-2
U3=-5
V1=7
V2=5
V3=9
E11= C11-(U1+V1)
E11=8-(0+7)
E11= 1
E21= C21-(U2-V1)
E21=6-(-2+7)
E21= 1

30. E23= C23-(U2+V3)
E23=12-(-2+9)
E23= 5
E32= C32-(U3+V2)
E32=7-(-5+5)
E32= 7
1 2 3 OFERTA
1 20 20 40
2 100 100
3 60 90 150
DEMANDA 60 120 110 290
VO=1060
3.-
1 2 3 OFERTA
1 50 50
2 25 150 175
3 25 100 125
DEMANDA 75 175 100 350
RUTA EN USO COSTO ECUACIÓN
11
21
22
32
33
6
7
5
5
2
U1+V1=6
U2+V1=7
U2+V2=5
U3+V2=5
U3+V3=2
58 9
6 3 12
2 7 4
36 2
7 5 9
4 5 2

31. U1=0
U1+V1=6 V1=6
U2+V1=7 U2=1
U2+V2=5 V2=4
U3+V2=5 U3=1
U3+V3=2 V3=1
U1=0
U2=1
U3=1
V1=6
V2=4
V3=1
E12= C12-(U1+V2)
E12=3-(0+4)
E12= -1
E13= C13-(U1+V3)
E13=2-(0+1)
E13= 1
E23= C23-(U2+V3)
E23=9-(1+1)
E23=7
E31= C31-(U3+V1)
E31=4-(1+6)
E31= -3
1 2 3 OFERTA

32. 1 50
-1 1
50
2 175
7
175
3
-3
25 100 125
DEMANDA 75 175 100 350
VO= 1450
4.-
1 2 3 OFERTA
A 80 80
B 20 140 160
C 10 180 190
DEMANDA 100 150 180 430
RUTA EN USO COSTO ECUACIÓN
11
21
22
32
33
8
4
9
8
7
U1+V1=8
U2+V1=4
U2+V2=9
U3+V2=8
U3+V3=7
U1=0
U1+V1=8 V1=8
U2+V1=4 U2=-4
U2+V2=9 V2=13
U3+V2=8 U3=-5
U3+V3=7 V3=12
U1=0
36 2
7 5 9
4 5 2
58 1
4 9 6
2 8 7

33. U2=-4
U3=-5
V1=8
V2=13
V3=12
E12= C12-(U1+V2)
E12=5-(0+13)
E12= -8
E13= C13-(U1+V3)
E13=1-(0+12)
E13= -11
E23= C23-(U2+V3)
E23=6-(-4+12)
E23= -2
E31= C31-(U3+V1)
E31=2-(-5+8)
E31= -1
1 2 3 OFERTA
1
-8
80
-11
80
2 100 60
-2
160
3
-1
10 180 190
DEMANDA 100 150 180 430
58 1
4 9 6
2 8 7

34. U1=0
U1+V2=5 V2=5
U2+V1=4 V1=0
U2+V2=9 U2=4
U3+V2=8 U3=3
U3+V3=7 V3=4
U1=0
U2=4
U3=3
V1=0
V2=5
V3=4
E11= C11-(U1+V1)
E11=8-(0+0)
E11=8
E13= C13-(U1+V3)
E13=1-(0+4)
E13= -3
E23= C23-(U2+V3)
E23=6-(4+4)
E23= -2
E31= C31-(U3+V1)
E31=2-(3+0)
E31= -1
1 2 3 OFERTA
1
8 -3
80 80
2 100 60
-2
160
58 1
4 9 6

35. 3
-1
90 100 190
DEMANDA 100 150 180 430
U1=0
U1+V3=1 V3=1
U2+V1=4 V1=-3
U2+V2=9 U2=7
U3+V2=8 V2=2
U3+V3=7 U3=6
U1=0
U2=7
U3=6
V1=-3
V2=2
V3=1
E11= C11-(U1+V1)
E11=8-(0-3)
E11= 11
E12= C12-(U1+V2)
E12=5-(0+2)
E12= 3
E23= C23-(U2+V3)
E23=6-(7+1)
E23= -2
E31= C31-(U3+V1)
E31=2-(6-3)
E31= -1
2 8 7

36. 1 2 3 OFERTA
1
11 3
80 80
2 100
-2
60 160
3
-1
150 40 190
DEMANDA 100 150 180 430
U1=0
U1+V3=1 V3=1
U2+V1=4 V1=-1
U2+V3=6 U2=5
U3+V2=8 V2=2
U3+V3=7 U3=6
U1=0
U2=5
U3=6
V1=-1
V2=2
V3=1
E11= C11-(U1+V1)
E11=8-(0-1)
E11= 9
E12= C12-(U1+V2)
E12=5-(0+2)
E12= 3
E22= C22-(U2+V2)
E22=9-(5+2)
58 1
4 9 6
2 8 7

37. E22= 2
E31= C31-(U3+V1)
E31=2-(6-1)
E31= -3
1 2 3 OFERTA
1
9 3
80 80
2 60
2
100 160
3
-3
40 150 190
DEMANDA 100 150 180 430
U1=0
U1+V3=1 V3=1
U2+V1=4 V1=-1
U2+V3=6 U2=5
U3+V1=2 U3=3
U3+V2=8 V2=5
U1=0
U2=5
U3=3
V1=-1
V2=5
V3=1
E11= C11-(U1+V1)
E11=8-(0-1)
E11= 9
E12= C12-(U1+V2)
E12=5-(0+5)
58 1
4 9 6
2 8 7

38. E12=0
E22= C22-(U2+V2)
E22=9-(5+5)
E22= -1
E33= C33-(U3+V3)
E33=7-(3+1)
E33= 3
1 2 3 OFERTA
1
9 0
80 80
2
-1
60 100 160
3 100 90
3
190
DEMANDA 100 150 180 430
U1=0
U1+V3=1 V3=1
U2+V2=9 V2=4
U2+V3=6 U2=5
U3+V1=2 V1=-2
U3+V2=8 U3=4
U1=0
U2=5
U3=5
V1=-2
V2=4
V3=1
E11= C11-(U1+V1)
58 1
4 9 6
2 8 7

39. E11=8-(0-2)
E11= 10
E13= C13-(U1+V3)
E12=5-(0+1)
E12= 4
E21= C21-(U2+V1)
E21=4-(5-2)
E21= 1
E33= C33-(U3+V3)
E33=7-(5+1)
E33= 1
1 2 3 OFERTA
1 80 80
2 60 100 160
3 100 90 190
DEMANDA 100 150 180 430
VO=2140
5.-
1 2 3 OFERTA
1 100 100
2 50 50 100
3 100 100 200
58 1
4 9 6
2 8 7
57 3
2 3 9
5 4 1

40. DEMANDA 150 150 100 400
RUTA EN USO COSTO ECUACIÓN
11
21
22
32
33
7
2
3
4
1
U1+V1=7
U2+V1=2
U2+V2=3
U3+V2=5
U3+V3=1
U1=0
U1+V1=7 V1=7
U2+V1=2 U2=-5
U2+V2=3 V2=8
U3+V2=5 U3=-3
U3+V3=1 V3=4
U1=0
U2= -5
U3=-3
V1=7
V2=8
V3=4
E12= C12-(U1+V2)
E12=5-(0+8)
E12= -3
E13= C13-(U1+V3)
E13=3-(0+4)
E13= -1
E23= C23-(U2+V3)
E23=9-(-5+4)
E23= 10
E31= C31-(U3+V1)

41. E31=5-(-3+7)
E31= 1
1 2 3 OFERTA
1 50
-3
50
-1
100
2 100
10
100
3
1
100 100 200
DEMANDA 150 150 100 400
U1=0
U1+V1=7 V1=7
U1+V2=5 V2=5
U2+V1=2 U2=-5
U3+V2=4 U3=-1
U3+V3=1 V3= 2
U1=0
U2=-5
U3=-1
V1=7
V2=5
V3=2
E13= C13-(U1+V3)
E13=3-(0+2)
E13= 1
E22= C22-(U2+V2)
E22=3-(-5+5)
E22= 3
E23= C23-(U2+V3)
57 3
2 3 9
5 4 1

42. E23=9-(-5+2)
E23= 12
E31= C31-(U3+V1)
E31=5-(-1+7)
E31= -1
1 2 3 OFERTA
1 100
1
100
2 100
3 12
100
3
-1
50 50 100 200
DEMANDA 150 150 100 400
U1=0
U1+V2=5 V2=5
U2+V1=2 U2=-4
U3+V1=5 V1=6
U3+V2=4 U3=-1
U3+V3=1 V3=2
U1=0
U2=-4
U3=-1
V1=6
V2=5
V3=2
E11= C11-(U1+V1)
E11=7-(0+6)
E11= 1
E13= C13-(U1+V3)
E13=3-(0+2)
57 3
2 3 9
5 4 1

43. E13= 1
E22= C22-(U2+V2)
E22=3-(-4+5)
E22= 2
E23= C23-(U2+V3)
E23=9-(-4+2)
E23= 11
1 2 3 OFERTA
1 100
1
100
2 100
3 12
100
3
-1
50 50 100 200
DEMANDA 150 150 100 400
REGLAS DE DERIVADAS
SUMA
PRODUCTO POR
UN NÚMERO
PRODUCTO
COCIENTE
COMPOSICIÓN
(Regla de la
cadena)
POTENCIA
57 3
2 3 9
5 4 1

44. TRIGONOMÉTRIC
A
FUNCIONES
ARCO
(Inversa o recíproca
de las
trigonométricas)
EXPONENCIALES
LOGARÍTMICAS
PROGRAMACIÓN CUADRÁTICA
La programación cuadrática (QP) es el nombre que se le da a un procedimiento
que minimiza una función cuadrática de n variables sujeta a m restricciones
lineales de igualdad o desigualdad. Un programa cuadrático es la forma más
simple de problema no lineal con restricciones de desigualdad. La importancia de
la programación cuadrática es debida a que un gran número de problemas
aparecen de forma natural como cuadráticos (optimización por mínimos
cuadrados, con restricciones lineales), pero además es importante porque aparece
como un su problema frecuentemente para resolver problemas no lineales más

45. complicados. Las técnicas propuestas para solucionar los problemas cuadráticos
tienen mucha similitud con la programación lineal.
Específicamente cada desigualdad debe ser satisfecha como igualdad. El
problema se reduce entonces a una búsqueda de vértices exactamente igual que
se hacía en programación lineal.
Consiste en maximizar o minimizar una función a través de un modelo matemático
extraído de un problema real que posea cualquier organización.
La función que se va a minimizar o maximizar esto quiere decir la manera óptima
en que un problema puede ser resuelto y esto a su vez minimiza costos y
maximiza las ganancias. Estos problemas vienen dados por funciones objetivo que
son las que vamos a maximizar o minimizar y por algunas restricciones dadas por
el contexto del problema, las restricciones pueden ser con o sin potencia, es decir,
con exponente o sin él.