Este documento presenta algunos conceptos fundamentales sobre límites, continuidad y asintotas de funciones. Resume los teoremas del límite de sen(x)/x cuando x tiende a cero y de (1-cos(x))/x cuando x tiende a cero. Explica las condiciones para que una función sea continua en un punto y cómo determinar las asintotas verticales y horizontales de una función dada por su gráfica. Proporciona ejemplos resueltos de cálculo de límites y determinación de continuidad y asintotas.

1. REPÚBLICA BOLIVARIANA DE VENEZUELA.
MINISTERIO DEL PODER POPULAR PARA LA EDUCACIÓN UNIVERSITARIA.
UNIVERSIDAD YACAMBÚ.
Bastidas Laura. ACP-133-00562
Teixeira Nelson. ACP-133-00729

2. Se pueden resolver aplicando un límite notable o una identidad
trigonométrica y en algunos casos se debe aplicar ambas operaciones.
Sin embargo a veces es necesario realizar algunas operaciones
algebraicas como multiplicar y dividir por un número, factorizar, multiplicar
por la conjugada o aplicar las propiedades de los límites.
RECORDEMOS
𝜋 rad= 180°
TEOREMA
1) lim
𝑥→0
sen 𝑥
𝑥
= 1
2) lim
𝑥→0
1−cos 𝑥
𝑥
= 0

3. 1) E f(a) Que el punto x = a tenga imagen.
2) E lim
𝑥→𝑎
f(x) Que exista el límite de la función en el punto x = a.
3) f(x)= lim
𝑥→𝑎
f(x) Que la imagen del punto coincida con el límite
de la función en el punto.
Se dice que una función f(x) es continua en un punto
x = a si y sólo si se cumplen las tres condiciones siguientes:
Si al menos una de las condiciones se deja de
cumplir, entonces la función no es continua.

4. Una asíntota, es una recta que se encuentra asociada a la gráfica de algunas
curvas y que se comporta como un límite hacia el cual la gráfica se aproxima
indefinidamente, pero nunca lo toca y mucho menos lo salta.
En general, la recta puede tener
cualquier orientación, sin embargo,
practicaremos las siguientes. Son rectas verticales asociadas a
la función, se encuentran presentes
únicamente en funciones racionales
de la forma 𝑓(𝑥)=
𝑔(𝑥)
ℎ(𝑥)
(al igual
que las horizontales), y su resultado
siempre debe ser +∞ ó -∞.
Asíntotas Verticales
Asíntotas Horizontales
Se determinan haciendo que la
variable independiente “x” tienda al
infinito, lo que trae como
consecuencia, que la función tienda a
un valor determinado fijo, al que
nunca va a llegar y mucho menos
sobrepasar.

5. 1) Si 𝑓(𝑥)=
−4 𝑠𝑖 𝑥 − 2
𝑥3
2
𝑠𝑖 − 2 ≤ 𝑥 < 2
𝑥 − 1 𝑠𝑖 𝑥 ≥ 2
Hallar:
𝑎) lim
𝑥→−2
f(x) 𝑏) lim
𝑥→2
f(x)
Resolvemos.
𝑎) lim
𝑥→−2
f(x)
lim
𝑥→−2
+
𝑥3
2
=
(−2)3
2
=
−8
2
= -4
lim
𝑥→−2
− -4 = -4
Entonces, como
lim
𝑥→−2
+ f(x) = lim
𝑥→−2
− f(x)
⟹ lim
𝑥→−2
f(x) = -4
𝑏) lim
𝑥→2
f(x)
lim
𝑥→2
+ x-1 = 2-1 = 1
lim
𝑥→2
−
𝑥3
2
=
23
2
=
8
2
= 4
Como lim
𝑥→2
+ f(x) ≠ lim
𝑥→2
− f(x)
entonces 𝑙𝑖𝑚
𝑥→2
f(x) no existe.

6. 2) Hallar
Resolvemos.
Sea 𝑦 = 𝑥 −
𝜋
6
⇒ 𝑥 = 𝑦 +
𝜋
6
Sea 𝑥 →
𝜋
6
⇒ 𝑦 → 0
lim
𝑦→0
𝑆𝑒𝑛𝑦
𝐶𝑜𝑠𝑦.𝑐𝑜𝑠
𝜋
6
−𝑠𝑒𝑛𝑦.𝑠𝑒𝑛
𝜋
6
−
3
2
lim
𝑦→0
𝑆𝑒𝑛𝑦
𝐶𝑜𝑠𝑦.
3
2
−𝑠𝑒𝑛𝑦.
1
2
−
3
2
lim
𝑦→0
𝑆𝑒𝑛𝑦
3
2
𝐶𝑜𝑠𝑦−
3
2
−
1
2
.𝑠𝑒𝑛𝑦
lim
𝑥→
𝜋
6
𝑆𝑒𝑛 𝑥 −
𝜋
6
𝐶𝑜𝑠𝑥 −
3
2
lim
𝑦→0
𝑆𝑒𝑛𝑦
𝐶𝑜𝑠 𝑦.𝑐𝑜𝑠
𝜋
6
−
3
2
lim
𝑦→0
𝑆𝑒𝑛𝑦
3
2
𝐶𝑜𝑠𝑦 − 1 −
1
2
𝑠𝑒𝑛𝑦
lim
𝑦→0
𝑆𝑒𝑛𝑦
𝑦
3
2
𝐶𝑜𝑠𝑦 − 1 −
1
2
𝑠𝑒𝑛𝑦
𝑦
lim
𝑦→0
𝑆𝑒𝑛𝑦
𝑦
3
2
𝐶𝑜𝑠𝑦 − 1
𝑦
−
1
2
𝑠𝑒𝑛𝑦
𝑦
lim
𝑦→0
𝑠𝑒𝑛𝑦
𝑦
3
2
lim
𝑦→0
𝐶𝑜𝑠𝑦 − 1
𝑦
−
1
2
lim
𝑦→0
𝑠𝑒𝑛𝑦
𝑦
1
3
2
. 0 −
1
2
. 1
= 1
0−
1
2
=
1
−
1
2
= -2

7. 3) Hallar lim
𝑥→0
1 − 𝑐𝑜𝑠2𝑥
4𝑥2
𝑆𝑒𝑎 𝜃 = 2𝑥
𝑆𝑖 𝑥 → 0 ⇒ 𝜃 → 0
Resolvemos.
lim
𝑥→0
1 − 𝑐𝑜𝑠2𝑥
(2𝑥)2
lim
𝑥→𝜃
1 − 𝑐𝑜𝑠𝜃
𝜃2
lim
𝑥→𝜃
1 − 𝑐𝑜𝑠𝜃 1 + 𝑐𝑜𝑠𝜃
𝜃2(1+𝑐𝑜𝑠𝜃)
lim
𝑥→𝜃
1 − 𝑐𝑜𝑠2 𝜃
𝜃2(1+𝑐𝑜𝑠𝜃)
lim
𝑥→𝜃
𝑠𝑒𝑛2
𝜃
𝜃2(1+𝑐𝑜𝑠𝜃)
lim
𝑥→𝜃
𝑠𝑒𝑛𝜃
𝜃
. lim
𝑥→𝜃
𝑠𝑒𝑛𝜃
𝜃
. lim
𝑥→𝜃
1
1 + cos𝜃
1.1. 1
1+cos(0)
1
1+1
=
1
2

8. 4) Hallar a y b sabiendo que la siguiente función es continua en -2
𝑓 𝑥
=
𝑥3, 𝑠𝑖 𝑥 ≤ −2
𝑘𝑥2
− 2𝑥, 𝑠𝑖 𝑥 > −2
Como la función es continua en -2, entonces es continua por la derecha
y por la izquierda de -2
f es continua por la derecha de -2, entonces:
𝑓 −2 = lim
𝑥→−2
+ 𝑓(x)
lim
𝑥→−2
+ 𝑘𝑥2 − 2𝑥(−2)3
=
−8 = 𝑘 −2 2
− 2 −2
−8 = 4𝑘 + 4
4𝑘 = −8 − 4
4𝑘 = −12
𝑘 =
−12
4
Resolvemos.
𝑘 = −3

9. 5) Hallar las asíntotas verticales y horizontales de la gráfica de la ecuación
𝑥𝑦2-𝑦2-4x-8= 0
Resolvemos.
“Despejamos y”
𝑥𝑦2
-𝑦2
-4x-8=0
⟹ 𝑥𝑦2
-𝑦2
= 4𝑥 + 8
⟹ 𝑦2(𝑥 − 1) = 4𝑥 + 8
𝑦2 =
4𝑥 + 8
𝑥 − 1
𝑦 = ±
4𝑥+8
𝑥−1
La gráfica de la función es la unión
de las funciones:
𝑓(𝑥)=
4𝑥+8
𝑥−1
y 𝑔(𝑥)= −
4𝑥+8
𝑥−1
𝐷𝑜𝑚𝑓 𝑥 y 𝐷𝑜𝑚𝑔 𝑥 son iguales:
4𝑥+8
𝑥−1
≥ 0 ⟹
4(𝑥+2)
𝑥−1
≥ 0
⟹
𝑥+2
𝑥−1
≥ 0
Raíces del numerador: x+2= 0 ⟹ 𝑥 = −2
Raíces del denominador: x-1= 0 ⟹ 𝑥 = 1
+ + + - - - + + +
−∞ +∞−𝟐 𝟏
X= -3 ⟹
−3+2
−3−1
=
−1
−4
= +
X= 0 ⟹
0+2
0−1
=
2
−1
= -
X= 2 ⟹
2+2
2−1
=
4
1
= +

10. 𝐷𝑜𝑚𝑓 𝑥 = 𝐷𝑜𝑚𝑔 𝑥 = (−∞, -2] U (1, +∞)
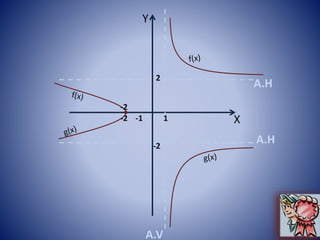
Asíntotas verticales (A.V)
El posible punto que origina A.V es x= 1
Como la función no esta definida en los puntos próximos y a la derecha de 1, entonces
sólo calculamos los límites a la derecha de ambas funciones.
lim
𝑥→1
+ 4𝑥 + 8 = 4.1 + 8 = 12 > 0 y lim
lim
𝑥→1
+ 𝑥 − 1 = 1 − 1
lim
𝑥→1
+f(x) = lim
𝑥→1
+
4𝑥 + 8
𝑥 − 1
Por otro lado lim
𝑥→1
+ g(x)= lim
𝑥→1
+
− f(x) = −∞
Entonces x= 1 es una Asíntota vertical.
= 0 positivamente, entonces:
= lim
𝑥→1
+
4𝑥+8
𝑥−1
=
2
0
= +∞
Asíntotas horizontales (A.H)
lim
𝑋→±∞
f x = lim
𝑋→±∞
4𝑥+8
𝑥−1
= lim
𝑋→±∞
4𝑥+8
𝑥
𝑥−1
𝑥

11. = lim
𝑋→±∞
4𝑥
𝑥
+
8
𝑥
𝑥
𝑥
−
1
𝑥
= lim
𝑋→±∞
4+
8
𝑥
1−
1
𝑥
= lim
𝑋→±∞
lim
𝑋→±∞
4+
8
𝑥
lim
𝑋→±∞
1−
1
𝑥
= lim
𝑋→±∞
lim
𝑋→±∞
4 + lim
𝑋→±∞
8
𝑥
lim
𝑋→±∞
1 − lim
𝑋→±∞
1
𝑥
=
4
1
= 2
lim
𝑋→±∞
g(x)= lim
𝑋→±∞
-f(x)= - lim
𝑋→±∞
f(x)= -2
Entonces Y=-2 y Y=2 son A.H

12. Y
X
A.H
A.H
A.V
-2
-2
-2
2
1-1
.

13. 6) Sea g(x)= 2𝑥2
+ 𝑥 Calcular: 𝑔′ 𝑥 por definición
Resolvemos.
𝑔′
𝑥 = lim
ℎ→0
𝑔 𝑥 + ℎ − 𝑔(𝑥)
ℎ
𝑔′ 𝑥 = lim
ℎ→0
2(𝑥 + ℎ)2
+ 𝑥 + ℎ − (2𝑥2
+ 𝑥)
ℎ
𝑔′ 𝑥 = lim
ℎ→0
2 𝑥2
+ 2𝑥ℎ + ℎ2
+ 𝑥 + ℎ − 2𝑥2
− 𝑥
ℎ
𝑔′ 𝑥 = lim
ℎ→0
2𝑥2
+ 4𝑥ℎ + 2ℎ2
+ 𝑥 + ℎ − 2𝑥2
− 𝑥
ℎ
𝑔′ 𝑥 = lim
ℎ→0
4𝑥ℎ + 2ℎ2
+ ℎ
ℎ
𝑔′ 𝑥 = lim
ℎ→0
ℎ(4𝑥 + 2ℎ + 1)
ℎ
𝑔′
𝑥 = lim
ℎ→0
4𝑥 + 2ℎ + 1 = 4𝑥 + 2 0 + 1 = 4𝑥 + 1

14. 7) Hallar a y b para que la función dada sea continua en su dominio
𝑓 𝑥 =
−2, 𝑠𝑖 𝑥 < −1
𝑎𝑥 + 𝑏, 𝑠𝑖 − 1 ≤ 𝑥 < 3
2, 𝑠𝑖 𝑥 ≥ 3
Resolvemos.
Como la función es continua en su dominio, tenemos:
𝑎) lim
𝑥→−1
𝑓 𝑥 𝑒𝑥𝑖𝑠𝑡𝑒 ⇔ lim
𝑥→−1
+ 𝑓 𝑥 lim
𝑥→−1
− f(x)
lim
𝑥→−1
+ (ax+b)= lim
𝑥→−1
− (-2)
𝑎 −1 + 𝑏 = −2
−𝑎 + 𝑏 = −2
𝑏) lim
𝑥→3
𝑓 𝑥 𝑒𝑥𝑖𝑠𝑡𝑒 ⇔ lim
𝑥→3
+ f(x)= lim
𝑥→3
− f(x)
lim
𝑥→3
+ 2= lim
𝑥→3
− (ax+b)
2= a(3+b)
1
3a+b=2 2
Formamos un sistema de
ecuaciones con 1 y 2
3
1
−𝑎 + 𝑏 = −2
3𝑎 + 𝑏 = 2
⇒
−3𝑎 + 3𝑏 = −6
3𝑎 + 𝑏 = 2
4b= -4
b=
−4
4
⇒ 𝑏 = −1

15. Sustituyendo b=1 en ecuación 2
3a+b= 2
3a+(-1)=2
3a-1=2
3a=2+1
3a=3
3a=
3
3
a=1
Los valores son; a=1 y b=-1

16. No permitas que nadie diga que eres
incapaz de hacer algo. Si tienes un sueño,
debes conservarlo. Si quieres algo, sal a
buscarlo, y punto. ¿Sabes?, las personas
que no logran conseguir sus sueños suelen
decirle a los demás que tampoco podrán
cumplir los suyos. Con dedicación, todo se
puede.
Esperamos habernos dado a entender, y servirles de ayuda, gracias.