Descargado 151 veces
Subido porJair Ospino Ardila
Derivada de funciones trigonometricas
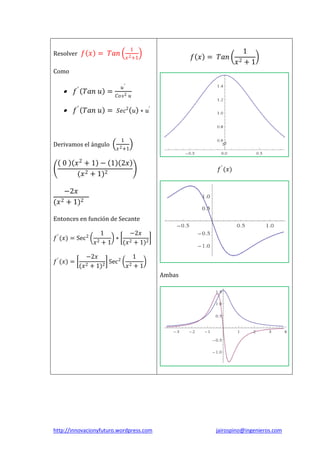
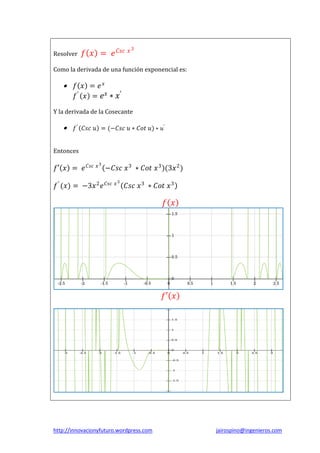
El documento presenta una guía sobre el cálculo diferencial de funciones trigonométricas, incluyendo identidades, tablas de derivadas y ejemplos resueltos. Se abordan derivadas de funciones como seno, coseno, tangente y sus inversas, además de derivadas de productos y cocientes. También se incluyen ejercicios prácticos con soluciones detalladas para facilitar la comprensión del tema.
Más contenido relacionado
Similar a Derivada de funciones trigonometricas
Derivada de funciones trigonometricas
- 1. Cálculo Diferencial Derivada deFunciones Trigonométricas G.IV. En esta guía veremos Identidades, Tablas para Derivadas y Ejercicios resueltos de las Funciones Trigonométricas. Innovación y Futuro Jair Ospino Ardila
- 2. Propiedades – IdentidadesTrigonométricas 𝑠𝑒𝑛2 𝑥 + cos2 𝑥 = 1 Tabla de Derivadas Nombre Funciones Seno Coseno Tangente Cotangente Secante Cosecante ArcoSeno ArcoCoseno ArcoTangente Nomenclatura 𝑆𝑒𝑛 𝑢 𝐶𝑜𝑠 𝑢 Derivadas 𝐶𝑜𝑠 𝑢 ∗ 𝑢′ −𝑆𝑒𝑛 𝑢 ∗ 𝑢′ 𝑇𝑎𝑛 𝑢 𝑆𝑒𝑐 2 𝑢 ∗ 𝑢′ o también 𝐶𝑜𝑡 𝑢 ( −𝐶𝑠𝑐 2 𝑢 ∗ 𝑢′ ) o también 𝑆𝑒𝑐 𝑢 𝐶𝑠𝑐 𝑢 𝑢′ 𝑆𝑒𝑐 𝑢 ∗ 𝑇𝑎𝑛 𝑢 ∗ 𝑢′ −𝐶𝑠𝑐 𝑢 ∗ 𝐶𝑜𝑡 𝑢 ∗ 𝑢′ 𝑢′ 𝐴𝑟𝑐𝑠𝑒𝑛 𝑢 𝐴𝑟𝑐𝑐𝑜𝑠 𝑢 𝐴𝑟𝑐𝑡𝑎𝑛 𝑢 http://innovacionyfuturo.wordpress.com 𝐶𝑜𝑠2 (𝑢) −𝑢′ 𝑆𝑒𝑛2 (𝑢) 1 − 𝑢2 −𝑢′ 1 − 𝑢2 𝑢′ 2+1 𝑢 jairospino@ingenieros.com
- 3. Resolver 𝑓 𝑥= 𝑠𝑒𝑛 3𝑥 𝑓 𝑥 = 𝑠𝑒𝑛 3𝑥 Como 𝑓 ′ (𝑠𝑒𝑛 𝑢) = 𝐶𝑜𝑠 𝑢 ∗ 𝑢′ Entonces 𝑓′ 𝑥 = 𝐶𝑜𝑠 3𝑥 ∗ (3) 𝑓′ 𝑥 = 3𝐶𝑜𝑠 3𝑥 𝑓′ 𝑥 = 3𝐶𝑜𝑠 3𝑥 𝑈𝑛𝑖𝑑𝑎𝑠 http://innovacionyfuturo.wordpress.com jairospino@ingenieros.com
- 4. Resolver 𝑓 𝑥= 𝐶𝑜𝑠 𝑥 3 𝑓 𝑥 = 𝐶𝑜𝑠 𝑥 3 Como 𝑓 ′ 𝑐𝑜𝑠 𝑢 = −𝑆𝑒𝑛 𝑢 ∗ 𝑢′ Entonces 𝑓 ′ 𝑥 = −𝑆𝑒𝑛 𝑥 3 ∗ 3𝑥 2 𝑓 ′ (𝑥) = −3𝑥 2 𝑆𝑒𝑛 𝑥 3 𝑓 ′ (𝑥) = −3𝑥 2 𝑆𝑒𝑛 𝑥 3 Ambas http://innovacionyfuturo.wordpress.com jairospino@ingenieros.com
- 5. Resolver 𝑓 𝑥= 𝐶𝑜𝑠 3 𝑥 𝑓 𝑥 = 𝐶𝑜𝑠 3 𝑥 Podemos reescribir esta función de la siguiente manera 𝑓 𝑥 = 𝐶𝑜𝑠 𝑥 3 Como 𝑑𝑦 𝑓 ′ 𝑐𝑜𝑠 𝑢 = −𝑆𝑒𝑛 𝑢 ∗ 𝑢′ 𝑑𝑥 𝑥 𝑛 = 𝑛𝑥 𝑛−1 ∗ 𝑥 ′ 𝑓 ′ 𝑥 = −3𝑆𝑒𝑛 Entonces 𝑓′ 𝑥 = 3 𝐶𝑜𝑠 𝑥 𝑓 ′ 𝑥 = −3𝑆𝑒𝑛 2 𝑥 ∗ 𝐶𝑜𝑠2 𝑥 ∗ (−𝑆𝑒𝑛 𝑥 ) 𝑥 ∗ 𝐶𝑜𝑠2 𝑥 Ambas http://innovacionyfuturo.wordpress.com jairospino@ingenieros.com
- 6. 1 Resolver 𝑓 𝑥= 𝑇𝑎𝑛 𝑓 𝑥 = 𝑇𝑎𝑛 𝑥 2 +1 1 𝑥2 + 1 Como 𝑢′ 𝑓 ′ 𝑇𝑎𝑛 𝑢 = 𝑓 ′ 𝑇𝑎𝑛 𝑢 = 𝑆𝑒𝑐2 𝑢 ∗ 𝑢′ Derivamos el ángulo 0 𝐶𝑜𝑠 2 𝑢 1 𝑥 2 +1 𝑥 2 + 1 − 1 2𝑥 (𝑥 2 + 1)2 𝑓 ′ (𝑥) −2𝑥 (𝑥 2 + 1)2 Entonces en función de Secante 𝑓 ′ (𝑥) = Sec 2 𝑓 ′ (𝑥) = 𝑥2 1 −2𝑥 ∗ 2 + 1)2 +1 (𝑥 −2𝑥 1 Sec 2 2 2 + 1) 𝑥 +1 (𝑥 2 Ambas http://innovacionyfuturo.wordpress.com jairospino@ingenieros.com
- 7. Resolver 𝑓 𝑥= 𝑒 −𝑥 ∗ 𝑆𝑒𝑛 2𝑥 𝑓 𝑥 = 𝑒 −𝑥 ∗ 𝑆𝑒𝑛 2𝑥 Como la derivada de un producto es: 𝑓 𝑥 = 𝑚∗ 𝑢 𝑓 ′ 𝑥 = 𝑚′ ∗ 𝑢 + 𝑚 ∗ 𝑢′ 𝑓 ′ (𝑠𝑒𝑛 𝑢) = 𝐶𝑜𝑠 𝑢 ∗ 𝑢′ Entonces 𝑓′ 𝑥 𝑓′ 𝑥 = −1 𝑒 −𝑥 ∗ 𝑆𝑒𝑛 2𝑥 + 𝑒 −𝑥 𝐶𝑜𝑠 2𝑥 ∗ (2) 𝑓 ′ (𝑥) = −𝑒 −𝑥 𝑆𝑒𝑛 2𝑥 + 2𝑒 −𝑥 𝐶𝑜𝑠 2𝑥 Tomamos factor común 𝑒 −𝑥 𝑓 ′ 𝑥 = 𝑒 −𝑥 2𝐶𝑜𝑠 2𝑥 − 𝑆𝑒𝑛 2𝑥 Ambas http://innovacionyfuturo.wordpress.com jairospino@ingenieros.com
- 8. Resolver 𝑓 𝑥= 𝑇𝑎𝑛3 25𝑥 4 Podemos reescribir esta función de la siguiente manera 𝑓 𝑥 = 𝑇𝑎𝑛 25𝑥 4 3 Como la derivada de una Potencia es: 𝑑𝑦 𝑑𝑥 𝑥 𝑛 = 𝑛𝑥 𝑛−1 ∗ 𝑥 ′ Entonces 𝑓 ′ (𝑥) = 3 𝑇𝑎𝑛 25𝑥 4 2 ∗ 𝑑𝑦 𝑑𝑥 𝑇𝑎𝑛 25𝑥 4 (A) En el paso anterior hemos dejado la derivada interna de la función indicada para resolverla en el siguiente paso con más calma Como la derivada de la Tangente es: 𝑓 ′ 𝑇𝑎𝑛 𝑢 = 𝑆𝑒𝑐2 𝑢 ∗ 𝑢′ Entonces 𝑑𝑦 4 𝑇𝑎𝑛 25𝑥 𝑑𝑥 = 𝑆𝑒𝑐 2 25𝑥 4 ∗ 𝑑𝑦 5𝑥 4 2 𝑑𝑥 Reemplazamos en (A) 𝑓 ′ (𝑥) = 3 𝑇𝑎𝑛 25𝑥 4 2 ∗ 𝑆𝑒𝑐 2 25𝑥 4 ∗ 𝑑𝑦 𝑑𝑥 25𝑥 4 (B) En el paso anterior hemos vuelto a dejar la derivada interna de la función indicada para resolverla en el siguiente paso con más calma Como la derivada de una función exponencial es: 𝑓 𝑥 = 𝑎𝑥 𝑓 ′ 𝑥 = 𝑎 𝑥 ∗ ln(𝑎) * x’ Entonces 𝑑𝑦 𝑑𝑥 25𝑥 4 4 = 25𝑥 ln 2 ∗ 𝑑𝑦 𝑑𝑥 5𝑥 4 Reemplazamos en (B) 𝑓 ′ (𝑥) = 3 𝑇𝑎𝑛 25𝑥 4 2 ∗ 𝑆𝑒𝑐 2 25𝑥 http://innovacionyfuturo.wordpress.com 4 4 ∗ 25𝑥 ln 2 ∗ 𝑑𝑦 5𝑥 4 𝑑𝑥 jairospino@ingenieros.com
- 9. Finalmente podemos apreciarque la última derivada indicada ya es muy sencilla. 𝑓 ′ (𝑥) = 3 𝑇𝑎𝑛 25𝑥 2 4 ∗ 𝑆𝑒𝑐 2 25𝑥 4 4 ∗ 25𝑥 ln 2 ∗ 20𝑥 3 Si ordenamos para mejor visibilidad 𝑓 ′ 𝑥 = 3 ∗ 20 𝑥 3 ∗ 𝑇𝑎𝑛2 25𝑥 4 4 ∗ 𝑆𝑒𝑐 2 25𝑥 𝑓 ′ 𝑥 = 60𝑥 3 ∗ 25𝑥 ∗ ln 2 ∗ 𝑇𝑎𝑛2 25𝑥 𝑓 𝑥 = 𝑇𝑎𝑛3 25𝑥 4 4 4 ∗ 25𝑥 ∗ ln 2 ∗ 𝑆𝑒𝑐 2 25𝑥 4 4 𝑓′ 𝑥 Ambos http://innovacionyfuturo.wordpress.com jairospino@ingenieros.com
- 10. Resolver 𝑓 𝑥 =𝑒 𝐶𝑠𝑐 𝑥3 Como la derivada de una función exponencial es: 𝑓 𝑥 = 𝑒𝑥 𝑓 ′ 𝑥 = 𝑒 𝑥 ∗ 𝑥′ Y la derivada de la Cosecante 𝑓 ′ 𝐶𝑠𝑐 𝑢 = (−𝐶𝑠𝑐 𝑢 ∗ 𝐶𝑜𝑡 𝑢) ∗ 𝑢′ Entonces 𝑓′ 𝑥 = 𝑒 𝐶𝑠𝑐 𝑥3 −𝐶𝑠𝑐 𝑥 3 ∗ 𝐶𝑜𝑡 𝑥 3 (3𝑥 2 ) 𝑓 ′ (𝑥) = −3𝑥 2 𝑒 𝐶𝑠𝑐 𝑥3 𝐶𝑠𝑐 𝑥 3 ∗ 𝐶𝑜𝑡 𝑥 3 𝑓 𝑥 𝑓′ 𝑥 http://innovacionyfuturo.wordpress.com jairospino@ingenieros.com
- 11. 𝑓 𝑥 = Resolver 𝑥2 +1 𝑥 𝑠𝑒𝑛 𝑥 Podemos reescribir esta función de la siguiente manera 𝑓 𝑥 = 𝑥2 + 1 1 ∗ 𝑥 𝑠𝑒𝑛 𝑥 Por identidad 𝐶𝑠𝑐 𝑥 = 1 𝑠𝑒𝑛 𝑥 Entonces 𝑓 𝑥 = 𝑥2 + 1 ∗ 𝐶𝑠𝑐 𝑥 𝑥 𝑓 𝑥 = 𝑥 2 ∗ 𝐶𝑠𝑐 𝑥 + 𝐶𝑠𝑐 𝑥 𝑥 Derivamos como un cociente como 𝑓 𝑥 = 𝑓′ 𝑥 = 𝑢 𝑧 𝑢′ ∗ 𝑧 − 𝑢 ∗ 𝑧′ 𝑧2 Derivada del Producto Como 𝑓 𝑥 = 𝑚∗ 𝑢 𝑥 2 ∗ 𝐶𝑠𝑐 𝑥 𝑓 ′ 𝑥 = 𝑚′ ∗ 𝑢 + 𝑚 ∗ 𝑢′ Procedemos a Derivar - 𝑓′ 𝑥 = 𝑓′ 𝑥 = Como en el numerador tenemos un producto que depende de la misma variable, tendremos que derivar como un producto primero antes de hacerlo como un cociente. 2𝑥 𝐶𝑠𝑐 𝑥 + 𝑥 2 −𝐶𝑠𝑐 𝑥 ∙ 𝐶𝑜𝑡 𝑥 + −𝐶𝑠𝑐 𝑥 ∙ 𝐶𝑜𝑡 𝑥 𝑥2 ∗ 𝑥− 1 𝑥 2 𝐶𝑠𝑐 𝑥 + 𝐶𝑠𝑐 𝑥 2𝑥 2 𝐶𝑠𝑐 𝑥 − 𝑥 3 𝐶𝑠𝑐 𝑥 ∙ 𝐶𝑜𝑡 𝑥 − 𝑥 𝐶𝑠𝑐 𝑥 ∙ 𝐶𝑜𝑡 𝑥 − 𝑥 2 𝐶𝑠𝑐 𝑥 − 𝐶𝑠𝑐 𝑥 𝑥2 Reducimos términos semejantes y eliminamos el corchete para apreciar mejor 𝑓′ 𝑥 = 𝑥 2 𝐶𝑠𝑐 𝑥 − 𝑥 3 𝐶𝑠𝑐 𝑥 ∙ 𝐶𝑜𝑡 𝑥 − 𝑥 𝐶𝑠𝑐 𝑥 ∙ 𝐶𝑜𝑡 𝑥 − 𝐶𝑠𝑐 𝑥 𝑥2 http://innovacionyfuturo.wordpress.com jairospino@ingenieros.com
- 12. Tomamos factor comúnCsc x 𝑓′ 𝑥 = 𝐶𝑠𝑐 𝑥 𝑥 2 − 𝑥 3 𝐶𝑜𝑡 𝑥 − 𝑥 𝐶𝑜𝑡 𝑥 − 1 𝑥2 Dentro del corchete tomamos factor común x Cot x 𝑓′ 𝑥 = 𝐶𝑠𝑐 𝑥 𝑥 2 − 𝑥 𝐶𝑜𝑡 𝑥 𝑥 2 + 1 − 1 𝑥2 Ordenamos para apreciar mejor 𝐶𝑠𝑐 𝑥 −𝑥 𝑥 2 + 1 ∙ 𝐶𝑜𝑡 𝑥 + 𝑥 2 − 1 𝑓′ 𝑥 = 𝑥2 𝑓′ 𝑥 = 𝐶𝑠𝑐 𝑥 − 𝑥 3 + 𝑥 ∙ 𝐶𝑜𝑡 𝑥 + 𝑥 2 − 1 𝑥2 Sacamos el signo menos del corchete 𝑓′ 𝑥 = − 𝐶𝑠𝑐 𝑥 𝑥 3 + 𝑥 ∙ 𝐶𝑜𝑡 𝑥 − 𝑥 2 + 1 𝑥2 𝑓 𝑥 Unidas 𝑓′ 𝑥 http://innovacionyfuturo.wordpress.com jairospino@ingenieros.com
- 13. 𝑓 𝑥 =ln Resolver 𝑥 2 𝐶𝑜𝑠 𝑥 2𝑥+1 3 Para resolver este ejercicio debemos utilizar una de las propiedades de los logaritmos. Dónde: ln 𝑗 𝑚 = ln 𝑗 – ln 𝑚 Si reemplazamos seria: 𝑓 𝑥 = ln 𝑥 2 𝐶𝑜𝑠 𝑥 − ln 2𝑥 + 1 3 Derivamos Como derivada de ln 𝑢 = 𝑢′ 𝑢 2𝑥 𝐶𝑜𝑠 𝑥 + 𝑥 2 (−𝑠𝑒𝑛 𝑥) 3 2𝑥 + 1 2 ∗ (2) 𝑓′ 𝑥 = − 𝑥 2 𝐶𝑜𝑠 𝑥 2𝑥 + 1 3 2𝑥 𝐶𝑜𝑠 𝑥 − 𝑥 2 𝑠𝑒𝑛 𝑥 6 2𝑥 + 1 2 𝑓′ 𝑥 = − 𝑥 2 𝐶𝑜𝑠 𝑥 2𝑥 + 1 3 2𝑥 𝐶𝑜𝑠 𝑥 𝑥 2 𝑠𝑒𝑛 𝑥 6 𝑓′ 𝑥 = 2 − 2 − 𝑥 𝐶𝑜𝑠 𝑥 𝑥 𝐶𝑜𝑠 𝑥 2𝑥 + 1 𝑓′ 𝑥 = 𝑓′ 𝑥 = 𝑓′ 𝑥 = 2 6 − tan 𝑥 − 𝑥 2𝑥 + 1 2 − 𝑥 tan 𝑥 𝑥 − 6 2𝑥 + 1 Identidad tan 𝑥 = 𝑠𝑒𝑛 𝑥 cos 𝑥 2 − 𝑥 tan 𝑥 2𝑥 + 1 − 6𝑥 𝑥 2𝑥 + 1 𝑓′ 𝑥 = 2 2𝑥 + 1 − 𝑥 tan 𝑥 2𝑥 + 1 − 6𝑥 𝑥 2𝑥 + 1 𝑓′ 𝑥 = 4𝑥 + 2 − 𝑥 tan 𝑥 2𝑥 + 1 − 6𝑥 𝑥 2𝑥 + 1 http://innovacionyfuturo.wordpress.com jairospino@ingenieros.com
- 14. 𝑓′ 𝑥 = 2− 𝑥 tan 𝑥 2𝑥 + 1 − 2𝑥 𝑥 2𝑥 + 1 𝑓 𝑥 𝑓′ 𝑥 Unidas http://innovacionyfuturo.wordpress.com jairospino@ingenieros.com
- 15. Resolver 𝑓 𝑥= 𝑎𝑟𝑐𝑠𝑒𝑛 1 − 2 𝑥 2 Como 𝑓′ 𝑎𝑟𝑐𝑠𝑒𝑛 𝑢 = 𝑢′ 1−𝑢2 Entonces −4𝑥 𝑓′ 𝑥 = 𝑓′ 𝑥 = 1 − 1 − 2 𝑥2 2 −4𝑥 1 − 1 − 4 𝑥 2 + 4𝑥 4 𝑓′ 𝑥 = −4𝑥 1 − 1 + 4 𝑥 2 − 4𝑥 4 𝑓′ 𝑥 = −4𝑥 4 𝑥 2 − 4𝑥 4 Factor común 𝑓′ 𝑥 = 𝑓′ 𝑥 = −4𝑥 4 𝑥2 − 𝑥4 −4𝑥 (22 ) 𝑥 2 − 𝑥 4 −4𝑥 𝑓′ 𝑥 = 2 𝑥2 − 𝑥4 𝑓′ 𝑥 = http://innovacionyfuturo.wordpress.com −2𝑥 𝑥2 − 𝑥4 jairospino@ingenieros.com