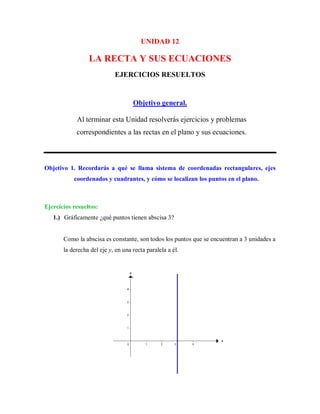
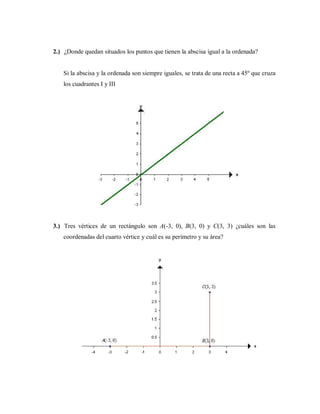
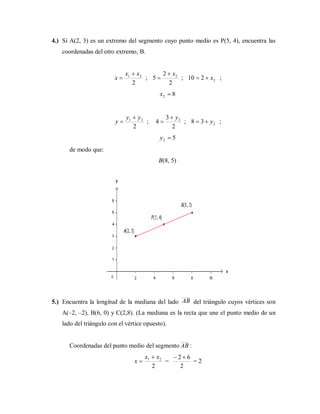
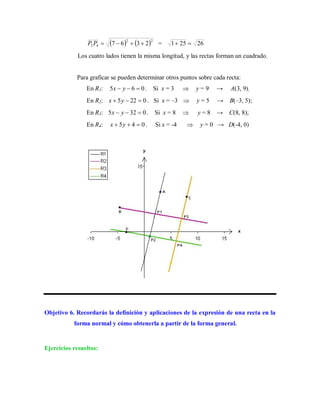
Este documento presenta ejercicios resueltos relacionados con rectas y sus ecuaciones en el plano cartesiano. Incluye seis objetivos con ejemplos de cómo calcular puntos, distancias, razones, ecuaciones de rectas y ángulos entre rectas. Los ejercicios cubren temas como sistemas de coordenadas, división de segmentos, pendientes, formas de ecuaciones de rectas y posiciones relativas entre rectas.

1. UNIDAD 12
LA RECTA Y SUS ECUACIONES
EJERCICIOS RESUELTOS
Objetivo general.
Al terminar esta Unidad resolverás ejercicios y problemas
correspondientes a las rectas en el plano y sus ecuaciones.
Objetivo 1. Recordarás a qué se llama sistema de coordenadas rectangulares, ejes
coordenados y cuadrantes, y cómo se localizan los puntos en el plano.
Ejercicios resueltos:
1.) Gráficamente ¿qué puntos tienen abscisa 3?
Como la abscisa es constante, son todos los puntos que se encuentran a 3 unidades a
la derecha del eje y, en una recta paralela a él.

2. 2.) ¿Donde quedan situados los puntos que tienen la abscisa igual a la ordenada?
Si la abscisa y la ordenada son siempre iguales, se trata de una recta a 45º que cruza
los cuadrantes I y III
3.) Tres vértices de un rectángulo son A(-3, 0), B(3, 0) y C(3, 3) ¿cuáles son las
coordenadas del cuarto vértice y cuál es su perímetro y su área?

3. Para completar el rectángulo, el otro vértice tiene que encontrarse al desplazarse en
ángulo recto a partir de los dos extremos, de modo que:
El punto buscado es D(-3, 3)
Perímetro: 2(6) + 2(3) = 12 + 6 = 18 unidades.
Área: b x h = 6 x 3 = 18 unidades cuadradas.
Objetivo 2. Recordarás y aplicarás las fórmulas para determinar la distancia entre
dos puntos cualesquiera del plano coordenado y las coordenadas del punto
que divide a un segmento en una razón r.
Ejercicios resueltos:
1.) Encuentra la distancia del origen al punto A(a, b)
   22
00  bad = 22
ba 
2.) Encuentra el valor de x necesario para que el punto P(x, 3) sea equidistante de los
puntos A(3, –2) y B(7, 4).

4.     22
323  xdPA
=   253
2
 x
   22
347  xdPB
=   17
2
 x
Para que P equidiste de A de B:
PBPA
dd 
  253
2
 x =   17
2
 x
  253
2
 x =   17
2
 x
114492569 22
 xxxx
25914914622
 xxxx
168 x
2x
El punto P(2, 3) equidista de los puntos A(3, –2) y B(7, 4).
3.) Si los extremos de un diámetro de una circunferencia son los puntos A(2, 3) y
B(5, 8), calcula la longitud de la circunferencia y el área del círculo que limita.
Diámetro =    22
3825 AB
d = 22
53  = 34
Circunferencia = d = 34 ; aproximadamente 18.3185 unidades
2
34
r ;
4
342
r
Área del círculo = 2
r =
4
34
 ; aproximadamente 26.7036 u2

5. 4.) Si A(2, 3) es un extremo del segmento cuyo punto medio es P(5, 4), encuentra las
coordenadas del otro extremo, B.
2
21 xx
x

 ;
2
2
5 2x
 ; 2210 x ;
82 x
2
21 yy
y

 ;
2
3
4 2y
 ; 238 y ;
52 y
de modo que:
B(8, 5)
5.) Encuentra la longitud de la mediana del lado AB del triángulo cuyos vértices son
A(–2, –2), B(6, 0) y C(2,8). (La mediana es la recta que une el punto medio de un
lado del triángulo con el vértice opuesto).
Coordenadas del punto medio del segmento AB :
2
21 xx
x

 =
2
62 
= 2

6. 2
21 yy
y

 =
2
02 
= –1
P(2, -1)
Distancia del punto P al vértice C
   22
8122 PC
d =  2
90  = 81 = 9
La mediana del lado AB al vértice C tiene una longitud de 9 unidades.
6.) Los extremos de un segmento son los puntos A(7, 4) y B(-1, -4) . Encuentra la razón
AP
PB
en que el punto P(1, –2) divide al segmento.
r
rxx
x



1
21
  211 rxxrx 
12 xrxrxx 
  xxxxr  12
2
1
xx
xx
r



 11
17


r =
2
6
= 3
La razón en que el punto P(1, –2) divide al segmento AB es 3.
(Un caso para este valor de r es que sea el último de los tres puntos que dividen al
segmento en cuatro partes iguales:
3
1
r  ).

7. Objetivo 4. Recordarás y aplicarás las diferentes formas de la ecuación de una recta,
dadas dos condiciones que la definen.
Ejercicios resueltos:
1.) Encuentra la ecuación de la recta que pasa por los puntos A(–2, –3) y B(5, 1)
 1
12
12
1 xx
xx
yy
yy 



   
 
  2
25
31
3 


 xy
 2
25
31
3 


 xy
 2
7
4
3  xy
   2437  xy
84217  xy
1347  xy
2.) Encuentra la ecuación de la recta que intersecta al eje de las ordenadas 7
unidades hacia abajo del origen y tiene una pendiente de
5
2

5
2
m ; b = –7;
bmxy 
7
5
2
y
3.) Tres vértices de un paralelogramo son los puntos A 





 0,
2
11
, B(0, 5) y C(–5, 8).
Encuentra las ecuaciones de los lados que pasan por AB y por BC.

8. Ecuación del lado que pasa por A y B:
2
11
a ; 5b ;
1
b
y
a
x
1
5
2
11


yx
1
511
2


yx
Ecuación del lado que pasa por B y C:
B(0, 5); C(–5, 8);
 1
12
12
1 xx
xx
yy
yy 



 0
05
58
5 


 xy
xy
5
3
5


5
5
3
 xy
4.) Encuentra la ecuación de una recta perpendicular a eje y, que pase por el punto
(h, k)
α = 0º; tan α = 0
 11 xxmyy 
 hxky  0
0 ky
ky 

9. Objetivo 5. Recordarás y aplicarás la forma general de la ecuación de una recta y las
condiciones necesarias y suficientes para las posiciones relativas entre dos
rectas en el plano.
Ejercicios resueltos:
1.) Determina la posición relativa de las rectas R1: 011014  yx y
R2: 3
14
5
2
 x
y
Para R1: 011014  yx
5
7
10
14
m
Para R2:
3
14
5
2
 x
y
03
214
5

y
x
       014314
2
14
14
5
14 










 y
x
04275  yx
7
5
7
5



B
A
m
2
1
1
R
R
m
m 
Por lo tanto, las rectas son perpendiculares.

10. 2.) Demuestra que las rectas R1: 065  yx , R2: 0225  yx ,
R3: 0325  yx y R4: 045  yx forman un cuadrado.
Posiciones relativas entre las rectas:
5
1
5
1 

Rm ;
5
1
2 Rm ; 5
1
5
3 

Rm ;
5
1
4 Rm
R1 y R3 son paralelas; R2 y R4, son paralelas.
R1 es perpendicular con R2 y con R4;
R3 es perpendicular con R2 y con R4.
Punto de intersección entre R1 y R2:
065  yx ;
65  xy
0225  yx ;
  022655  xx ;
0223026 x ;
26
52
x = 2
  625 y = 4 → P1(2, 4)
Con el mismo procedimiento, los otros puntos de intersección son:
R1 y R4: P2(1, –1)
R3 y R2: P3(7, 3)
R3 y R4: P4(6, –2)
Longitudes de los lados:
   22
21 1412 PP = 26251 
   22
31 3472 PP = 26125 
   22
42 2161 PP = 26125 

11.    22
43 2367 PP = 26251 
Los cuatro lados tienen la misma longitud, y las rectas forman un cuadrado.
Para graficar se pueden determinar otros puntos sobre cada recta:
En R1: 065  yx . Si x = 3  y = 9 → A(3, 9);
En R2: 0225  yx . Si x = –3  y = 5 → B(–3, 5);
En R3: 0325  yx . Si x = 8  y = 8 → C(8, 8);
En R4: 045  yx . Si x = -4  y = 0 → D(-4, 0)
Objetivo 6. Recordarás la definición y aplicaciones de la expresión de una recta en la
forma normal y cómo obtenerla a partir de la forma general.
Ejercicios resueltos:

12. 1.) Calcula la longitud del radio de la circunferencia con centro en el punto (2, 3) y que
es tangente a la recta 0334  yx
Radio de la circunferencia = distancia del centro de la circunferencia a la tangente.
1 1
2 2
Ax By C
d
A B
 

 
=
22
34
3)3(3)2(4


=
25
398 
=
5
20
= 4
radio = 4 (unidades de longitud)
2.) Calcula el área del triángulo cuyos vértices son P1(2, 1), P2(8, 2) y P3 (3, 6)
Base del triángulo: cualquiera de los tres lados, por ejemplo, 21PP . Usando la
ecuación de la recta que pasa por dos puntos dados:
 2
28
12
1 


 xy
 2
6
1
1  xy
266  xy
046  yx
Longitud de la base:
distancia  2
12
2
1221 )( yyxxPP  = 22
)12()28(  = 136  =
37
Altura del triángulo: distancia del otro vértice, P3 (3, 6), a la base:
1 1
2 2
Ax By C
d
A B
 

 
=
22
)6(1
4)6)(6(3


=
37
4363 
=
37
29
=
37
29

13. Área del triángulo =
2
hb
=
2
37
29
37 





=
2
29
(unidades de superficie)
3.) La distancia dirigida de la recta 01052  yx a un punto P es –3. Si la abscisa de
P es 2, encuentra su ordenada.
Distancia dirigida:
22
11
BA
CByAx
d



C < 0  signo del radical positivo, y para el punto P (2, y):
22
52
105)2(2
3



y
29
65
3


y
65)29)(3(  y
29365 y
La ordenada es:
5
2936 
y