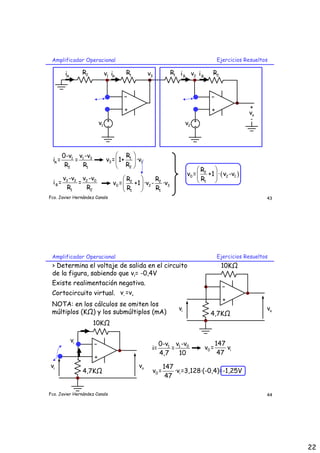
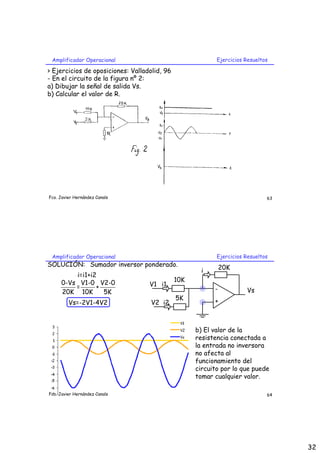
El documento trata sobre diferentes aplicaciones de amplificadores operacionales, incluyendo seguidores de tensión, amplificadores inversores y no inversores, sumadores inversores y no inversores ponderados, amplificadores con eliminación de nivel de continua, amplificadores diferenciales e instrumentales, amplificadores de intensidad con carga flotante y convertidores de corriente a tensión y de tensión a corriente. Explica el funcionamiento y características de cada circuito.