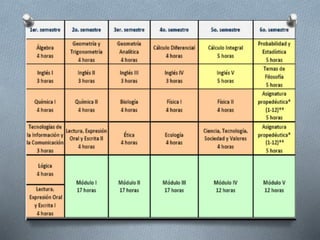
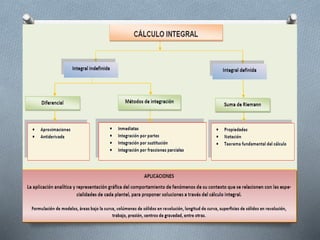
El documento presenta un programa de estudio para el cálculo integral, donde se analizan y resuelven problemas de la vida cotidiana mediante el teorema fundamental del cálculo y diversas técnicas de integración. Incluye un plan de evaluación, competencias a desarrollar y referencias bibliográficas relevantes. Además, ofrece materiales y enlaces relacionados con el cálculo para enriquecer el aprendizaje.

1. Cálculo Integral
Francisco Gurrola Ramos
CBTis 206
Agosto 2018

3. Propósito
Propósito. El estudiante analiza e interpreta las
relaciones entre las variables de problemas de la
vida cotidiana relacionadas con áreas, volúmenes,
etc., que impliquen variaciones en procesos
infinitos y los resuelva aplicando el teorema
fundamental del cálculo.

4. Programa de estudio

5. Estructura Curricular

6. Contenido
O Introducción
O Derivada
O Aplicaciones de la derivada
O Diferencial
O Aplicaciones de la diferencial
O Aproximaciones y error.
O Antiderivadas
O Integrales inmediatas
O Constante de integración
O Integrales definidas
O Teorema Fundamental del Cálculo
O Sumas de Riemann
O Movimiento rectilíneo
uniformemente acelerado
O Área entre dos curvas
O Volumen de sólidos en cascara y
rebanada.
O Trabajo mecánico y
termodinámico
O Presión y fuerza en fluidos.
O Centro de masa e inercia
O Integración por sustitución
O Integración por partes,
O Integración de fracciones.
O Integración de trigonometría,

8. Competencias
O G1.Se conoce y valora a sí mismo y aborda
problemas y retos teniendo en cuenta los
objetivos que persigue.G5.Desarrolla
innovaciones y propone soluciones a problemas a
partir de métodos establecidos.
O G8. Participa y colabora de manera efectiva en
equipos diversos.
M2Formula y resuelve problemas matemáticos,
aplicando diferentes enfoques.
M3.Explica e interpreta los resultados obtenidos
mediante procedimientos matemáticos y los
contrasta con modelos establecidos o situaciones
reales.

9. Plan de evaluación
30% Cuaderno con las construcciones y tareas
revisadas en evaluación formativa
20% Presentación apoyada con PPT, trípticos
y cartel didáctico
20% Calidad de la exposición (no leer,
mostrar dominio del tema)
20% Tareas de Khan Academy
10% Examen de conocimientos.

10. Bibliografía
O Granville (1998): "Cálculo diferencial e
Integral". Limusa, Trillas.
O Leithold L. (1998). El cálculo. 7ma. Edición.
Oxford University Presspp 296-469
O Zill, D. G.(2011). “Cálculo de una variable”.
Mc Graw Hill México pp 267-438
REFERENCIAS BIBLIOGRAFICAS
Granville (1998): "Cálculo diferencial e Integral". Limusa, Trillas.
Leithold L. (1998). El cálculo. 7ma. Edición. Oxford University Presspp 296-469
Zill, D. G.(2011). “Cálculo de una variable”. Mc Graw Hill México pp 267-438

11. Enlaces
O¿Qué es el Cálculo?
https://www.youtube.com/watch?v=U5aW5aR0qbU
O¿Qué es el Cálculo, intuitivamente ...?
https://www.youtube.com/watch?v=tmFYMb2MQW0
OHistoria del Cálculo
https://www.youtube.com/watch?v=JlAU4tHY2ow

12. Productos
OFormulario
OPlaneación
ODiagnóstico
OTarea 1 Habilidades Socioemocionales
OMapa conceptual
OLínea de tiempo
OErrores y aproximaciones
OAplicación de derivada
OProblemas de áreas

14. Mil gracias por su atención
De todas maneras, lo más maravilloso del 0 no es
sólo que sea un signo o un criterio, sino que es un
número en sí mismo. El único número natural que
sólo es menos que 1 es el 0. Pese a la existencia
del 0, la unidad de las reglas del cálculo no se ve
afectada. Más bien, el 0 refuerza aún más su
coherencia, hace más sólido su orden. Venga,
imagínatelo: un pajarillo está parado en la copa
de un árbol. Es un pájaro que canta con voz clara.
Tiene el pico precioso y unas alas con dibujos
hermosos. Antes de que se nos escape un
suspiro de fascinación, el pajarillo sale volando.
En la copa, ya no queda ni su sombra.
Únicamente las hojas secas estremecidas..