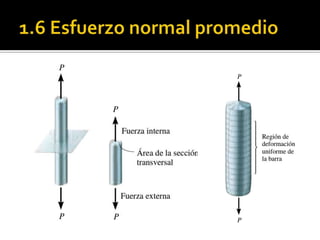
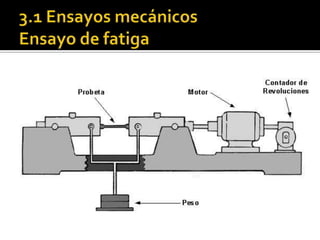
El documento describe conceptos básicos de resistencia de materiales, incluyendo esfuerzos, deformaciones, propiedades mecánicas y ensayos mecánicos. Explica que los esfuerzos incluyen tracción, compresión y corte, y que las deformaciones incluyen alargamiento y contracción. También describe cómo los ensayos mecánicos como la tracción son usados para determinar propiedades como el módulo de elasticidad y límites de fluencia y fractura de los materiales.

1. Diego Andrés Hincapié Zuluaga

2.  1. Esfuerzo
 2. Deformación unitaria
 3. Propiedades mecánicas

8.  Es cuando un fuerza por área unitaria actúa
normalmente a un elemento diferencial de área.
Fz
 z  lim
A0 A
Si la fuerza normal hala el elemento diferencial de área
se conoce como un esfuerzo de tracción o tensión.
Si la fuerza normal empuja el elemento diferencial de
área se conoce como esfuerzo de compresión.

9.  Es cuando un fuerza por área unitaria actúa
tangencialmente a un elemento diferencial
de área.
Fx
 zx  lim
A  0  A
Fy
 zy  lim
A  0  A

12.   FRZ   Fz
 dF    dA
A
P  A
P

A

13. V
 p r om 
A

16.   Fy  0
 zy  x y    zy  x y   0
  M x   zy  x y  z   yz  x z  y  0

 zy   zy  zy   yz

17.  zy   yz 
 zy   zy
 zy   zy   yz   zy  
 

18.  Es el esfuerzo máximo que se puede alcanzar
en un material para sea seguro.
 falla
FS 
Ffalla  perm
FS 
Fperm
 falla
FS 
 perm

23. s  s
 prom 
s

 prom 
s
s  s
  lim s  1    s
B  A a lo l arg o de n s

24. 
 nt   lim 
2 B  A a lo l arg o de n
C  A a lo l arg o de t

30.  Mediante los ensayos mecánicos se valoran con
exactitud las propiedades mecánicas.
Tipos de pruebas
 Estáticas
 Cíclicas
 De duración prolongada
 Producidas por impulsos
30

32. 32

33. 33

35. 35

38.  La resistencia de los materiales puede ser probada
halando hasta que falle.
Celda de carga
Probeta
Extensómetro
Los datos de fuerza son obtenidos de la Celda de carga
Los datos de deformación son obtenidos del Extensómetro

39. Comportamiento Comportamiento
teórico en el ensayo
Esfuerzo (Mpa)
Deformación unitaria (mm/mm)

40. Propiedades mecánicas que se pueden obtener
del ensayo de tracción:
•Módulo de elasticidad
•Limite proporcional
•Límite elástico convencional de 0.2 %
•Resistencia ultima a la tracción
•Porcentaje de alargamiento a fractura
•Porcentaje de estricción a fractura
•Modulo de resiliencia
•Modulo de tenacidad

41. l  lo A A
% alargamiento  100 %% estricción  0 100 % Esfuerzo último
lo Ao a la tracción
Estricción
Su
t Esfuerzo de
fluencia Esfuerzo
Limite elástico de
fractura
Esfuerzo (Mpa)
Sy
Endurecimiento
por deformación
 Limite proporcional
E

Modulo de
resiliencia
Modulo de
tenacidad
0.2%
Región Elástica Fluencia Endurecimiento por de formación Estricción
Deformación unitaria (mm/mm)

47.   E

49. U  WDeformación Densidad de energía de
deformación
U    W
 x y     z
U  
U   F ( z )dz  2
V x y z
Rango elástic0 1 12
u  
   x y      z 2 2 E
U   
2
1
U     x  y  z
2
1
U     V
2

50. 1  lp
2
1
ur   lp  lp 
2 2 E

52.    lat
 long   lat   
L L  long

53.   G
E
G
2 1   