La primera oración resume los tipos de vigas simple apoyadas y las cargas que se pueden aplicar, incluyendo cargas puntuales, uniformes y variables. La segunda oración resume las ecuaciones fundamentales para calcular la deflexión, pendiente, momento y cortante. La tercera oración indica que el documento proporciona ejemplos detallados para cada caso de carga aplicada a una viga simple apoyada.

1. Fórmulas de deformación de vigas www.vaxasoftware.com
Simbolo Magnitud Unidades
E·I Rigidez a flexión N·m2
, Pa·m4
y Deflexión, deformación, flecha m
θ Pendiente, giro -
x Posición del punto de estudio (distancia desde el origen) m
L Longitud de la viga (sin vano lateral) m
M Momento flector, flector, momento aplicado N·m
P Carga puntual, carga concentrada N
w Carga distribuida N/m
R Reacción N
V Esfuerzo cortante, cortante N
Viga simple apoyada - Carga uniforme en todo el vano
Deflexión )2(
24
3230
AB xLxL
EI
xw
y +−
−
=
EI
Lw
y
384
5 4
0
MAX
−
= para
2
L
x =
Pendiente )46(
24
3230
AB xLxL
EI
w
+−
−
=θ
EI
Lw
24
3
0
BA
−
=−= θθ
Momento )(
2
0
AB xL
xw
M −=
8
2
0
MAX
Lw
M = para
2
L
x =
Cortante )2(
2
0
AB xL
w
V −=
Reacciones
2
0
BA
Lw
RR ==

2. Viga simple apoyada - Carga uniforme en la mitad del vano
Deflexión )16249(
384
3230
AC xLxL
EI
xw
y +−
−
=
)17248(
384
32230
CB LxLLxx
EI
Lw
y −+−
−
=
Pendiente )64729(
384
3230
AC xLxL
EI
w
+−
−
=θ
)174824(
384
220
CB LLxx
EI
Lw
+−
−
=θ
EI
wL
128
3 3
A
−
=θ
EI
wL
384
7 3
B =θ
Momento )43(
8
20
AC xLx
w
M −= )(
8
20
CB LxL
w
M −=
Cortante )83(
8
0
AC xL
w
V −=
8
0
CB
Lw
V
−
=
AA RV = BB RV −=
Reacciones
8
3 0
A
Lw
R =
8
0
B
Lw
R =
Viga simple apoyada - Carga uniforme parcial en un lado
Deflexión:
)4244(
24
322222340
AC LxaLxxaLaLaa
LEI
xw
y +−++−
−
=
)264(
24
32222
2
0
CB xLxxaxLLa
LEI
aw
y +−++−
−
=
Pendiente:
)412644(
24
322222340
AC LxaLxxaLaLaa
LEI
w
+−++−
−
=θ
)6124(
24
222
2
0
CB xLxaL
LEI
aw
+−+
−
=θ
Momento:
)2(
2
220
AC LxaLxxa
L
w
M +−
−
= )(
2
2
0
CB xL
L
aw
M −=
Cortante:
)22(
2
20
AC LxaLa
L
w
V +−
−
=
L
aw
VVV
2
2
0
BCCB
−
===
Reacciones )2(
2
0
A aL
L
aw
R −=
L
aw
R
2
2
0
B =

3. Viga simple apoyada - Carga uniforme parcial
Deflexión x
EI
xR
y α+=
6
3
A
AC xax
EI
w
EI
xR
y α+−−= 40
3
A
CD )(
246
L
xL
EI
xLR
y
)(
6
)( 3
B
DB
−
+
−
=
β
Pendiente: αθ +=
EI
xR
2
2
A
AC αθ +−−= 30
2
A
CD )(
62
ax
EI
w
EI
xR
LEI
xLR β
θ −
−−
=
2
)( 2
B
DB
Momento xRM AAC = 20
ACD )(
2
ax
w
xRM −−=
)(BDB xLRM −=
Cortante ACAAC RVVV === )(0ACD axwRV −−=
BBDDB RVVV −===
Reacciones )2(
2
0
A bc
L
bw
R += )2(
2
0
B ba
L
bw
R +=
Siendo:
LEI
baLRLcREILbw
6
)(336 2
A
2
B
3
0 +−−−
=
β
α
EI
cRLcRbaRbwabw
24
812)(834 3
B
2
B
3
A
4
0
3
0 +−+−+
=β
Viga simple apoyada - Cargas uniformes parciales distintas a cada lado
Momento
2
2
1
AAC
xw
xRM −=
)2(
2
1
ACD ax
aw
xRM −−=
2
)(
)(
2
2
BDB
xLw
xLRM
−
−−=
Cortante:
xwRV 1AAC −= awRV 1ACD −= )(2BDB xLwRV −+−=
Reacciones:
L
cwaLaw
R
2
)2( 2
21
A
+−
=
L
awcLcw
R
2
)2( 2
12
B
+−
=

4. Viga simple apoyada - Carga uniformemente creciente en todo el vano
Deflexión )3107(
360
42240
AB xxLL
LEI
xw
y +−
−
=
EI
Lw
y
4
0
MAX 00652,0−= para x = 0,5193L
Pendiente )15307(
360
42240
AB xxLL
LEI
w
+−
−
=θ
EI
Lw
360
7 3
0
A
−
=θ
EI
Lw
45
3
0
B =θ
Momento )(
6
320
AB xxL
L
w
M −=
Cortante )3(
6
220
AB xL
L
w
V −=
Reacciones
6
0
A
Lw
R =
6
2 0
B
Lw
R =
Viga simple apoyada - Carga uniformemente creciente hacia el centro
Deflexión 2220
AC )45(
960
xL
LEI
xw
y −
−
=
2220
CB ))(45(
960
)(
xLL
LEI
xLw
y −−
−−
=
EI
Lw
y
120
4
0
MAX
−
= para
2
L
x =
Pendiente )4)(45(
192
22220
AC xLxL
LEI
w
−−
−
=θ
))(4)()(45(
192
22220
CB xLLxLL
LEI
w
−−−−=θ
EI
Lw
192
5 3
0
BA
−
=−= θθ
Momento )43(
12
320
AC xxL
L
w
M −=
))(43(
12
)( 220
CB xLL
L
xLw
M −−
−
=
Cortante )4(
4
220
AC xL
L
w
V −= ))(4(
4
220
CB xLL
L
w
V −−
−
=
Reacciones
4
0
BA
Lw
RR ==

5. Viga simple apoyada - Carga senoidalmente distribuida
Deflexión
L
x
EI
Lw
y
π
sen
π4
4
0
AB
−
=
EI
Lw
y 4
4
0
MAX
π
−
= para
2
L
x =
Pendiente
L
x
EI
Lw π
cos
π3
3
0
AB
−
=θ
EI
Lw
3
3
0
BA
π
−
=−= θθ
Momento
L
xLw
M
π
sen
π2
2
0
AB =
Cortante
L
xLw
V
π
cos
π
0
AB =
π
0
BA
Lw
VV =−=
Reacciones
π
0
BA
Lw
RR ==
Viga simple apoyada - Carga puntual en el centro
Deflexión )43(
48
22
AC xL
EI
Px
y −
−
=
))(43(
48
)( 22
CB xLL
EI
xLP
y −−
−−
=
EI
PL
yy
48
3
CMAX
−
== para
2
L
x =
Pendiente:
)4(
16
22
AC xL
EI
P
−
−
=θ )384(
16
22
CB LLxx
EI
P
+−
−
=θ
EI
PL
16
2
BA =−= θθ
Momento
2
AC
Px
M =
2
)(
CB
xLP
M
−
=
Cortante
2
AAC
P
VV ==
2
BCB
P
VV
−
==
Reacciones
2
BA
P
RR ==

6. Viga simple apoyada - Carga puntual en cualquier punto
Deflexión )(
6
222
AC xbL
LEI
Pbx
y −−
−
=
[ ]222
CB )(
6
)(
xLaL
LEI
xLPa
y −−−
−−
=
Pendiente:
)3(
6
222
AC xbL
LEI
Pb
−−
−
=θ [ ]222
CB )(3
6
xLaL
LEI
Pa
−−−=θ
LEI
bLPb
6
)( 22
A
−−
=θ )(
6
22
B aL
LEI
Pa
−=θ
Momento
L
Pbx
M =AC
L
xLPa
M
)(
CB
−
=
Cortante
L
Pb
VV == AAC
L
Pa
VV
−
== BCB
Reacciones
L
Pb
R =A
L
Pa
R =B
Viga simple apoyada - Dos cargas puntuales iguales situadas simétricamente
Deflexión )33(
6
22
AC xaaL
EI
Px
y −−
−
=
)33(
6
22
CD axLx
EI
Pa
y −−
−
=
[ ]22
DB )(33
6
)(
xLaaL
EI
xLP
y −−−
−−
=
)43(
24
22
MAX aL
EI
Pa
y −
−
= para
2
L
x =
Pendiente )(
2
22
AC xaaL
EI
P
−−
−
=θ )2(
2
CD xL
EI
Pa
−
−
=θ
[ ]22
DB )(
2
xLaaL
EI
P
−−−=θ
EI
aaLP
2
)( 2
BA
−−
=−= θθ
Momento PxM =AC PaM =CD )(DB xLPM −=
Cortante PV =AC 0CD =V PV −=DB
Reacciones PRR == BA
Viga simple apoyada - Dos cargas puntuales iguales situadas asimétricamente
Momento xRM AAC = )(ACD axPxRM −−=
)(BDB xLRM −=
Cortante AAC RV = PRV −= ACD BDB RV −=
Reacciones
L
baLP
R
)(
A
+−
=
L
abLP
R
)(
B
+−
=

7. Viga simple apoyada - Dos cargas puntuales desiguales situadas asimétricamente
Momento xRM AAC = )(1ACD axPxRM −−=
)(BDB xLRM −=
Cortante AAC RV = 1ACD PRV −= BDB RV −=
Reacciones
L
bPaLP
R 21
A
)( +−
=
L
aPbLP
R 12
B
)( +−
=
Viga simple apoyada - Momento antihorario en el lado derecho
Deflexión )(
6
220
AB xL
LEI
xM
y −
−
=
Pendiente )3(
6
220
AB xL
LEI
M
−
−
=θ
EI
LM
6
0
A
−
=θ
EI
LM
3
0
B =θ
Momento
L
xM
M 0
AB =
Cortante
L
M
V 0
AB =
Reacciones
L
M
R 0
A =
L
M
R 0
B
−
=
Viga simple apoyada - Momento antihorario en el lado izquierdo
Deflexión )32(
6
220
AB xLxL
LEI
xM
y +−=
EI
LM
y
39
2
0
MAX = para Lx ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛ −
=
3
33
Pendiente )362(
6
220
AB xLxL
LEI
M
+−=θ
EI
LM
3
0
A =θ
EI
LM
6
0
B
−
=θ
Momento )(0
AB xL
L
M
M −
−
=
Cortante
L
M
V 0
AB =
Reacciones
L
M
R 0
A =
L
M
R 0
B
−
=

8. Viga simple apoyada - Momento horario en el extremo izquierdo
Deflexión )32(
6
220
AB xLxL
LEI
xM
y +−
−
=
EI
LM
y
39
2
0
MAX
−
= para Lx ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛ −
=
3
33
Pendiente )362(
6
220
AB xLxL
LEI
M
+−
−
=θ
EI
LM
3
0
A
−
=θ
EI
LM
6
0
B =θ
Momento )(0
AB xL
L
M
M −=
Cortante
L
M
V 0
AB
−
=
Reacciones
L
M
R 0
A
−
=
L
M
R 0
B =
Viga simple apoyada - Momento antihorario en el centro
Deflexión )4(
24
220
AC xL
LEI
xM
y −
−
=
))(4(
24
)( 220
CB xLL
LEI
xLM
y −−
−
=
Pendiente )12(
24
220
AC xL
LEI
M
−
−
=θ
))(12(
24
220
CB LxL
LEI
M
−−=θ
)3(
6
220
A bL
LEI
M
−
−
=θ )3(
6
220
B aL
LEI
M
+−=θ
Momento
L
xM
M 0
AC = )(0
CB xL
L
M
M −
−
=
Cortante
L
M
V 0
AC =
L
M
V 0
CB =
Reacciones
L
M
R 0
A =
L
M
R 0
B
−
=

9. Viga simple apoyada - Momento antihorario en cualquier punto
Deflexión )3(
6
2220
AC xbL
LEI
xM
y −−
−
=
))(3(
6
)( 2220
CB xLaL
LEI
xLM
y −−−
−
=
Pendiente )33(
6
2220
AC xbL
LEI
M
−−
−
=θ
))(33(
6
2220
CB xLaL
LEI
M
−++−=θ
)3(
6
220
A bL
LEI
M
−
−
=θ )3(
6
220
B aL
LEI
M
+−=θ
Momento
L
xM
M 0
AC = )(0
CB xL
L
M
M −
−
=
Cortante
L
M
V 0
AC =
L
M
V 0
CB =
Reacciones
L
M
R 0
A =
L
M
R 0
B
−
=
Viga simple apoyada - Dos momentos distintos antihorario + horario en los extremos
Deflexión [ ]LMMxMM
LEI
xLx
y )2()(
6
)(
2121AB +−−
−−
=
Pendiente:
[ ])2)(2()23)((
6
1 2
21
2
21AB LLxMMLxxMM
LEI
−+−−−=θ
Momento [ ]121AB )(
1
LMxMM
L
M −−=
Cortante
L
MM
V 21
AB
−
=
Reacciones
L
MM
R 21
A
−
=
L
MM
R 12
B
−
=
Viga simple apoyada - Dos momentos distintos antihorario en los extremos
Deflexión [ ]LMMxMM
LEI
xLx
y )2()(
6
)(
2121AB −−+
−−
=
Pendiente:
[ ])2)(2()23)((
6
1 2
21
2
21AB LLxMMLxxMM
LEI
−−−−+=θ
Momento [ ]121AB )(
1
LMxMM
L
M −+=
Cortante
L
MM
V 21
AB
+
=
Reacciones
L
MM
R 21
A
+
=
L
MM
R 21
B
−−
=

10. Viga simple apoyada - Dos momentos iguales horario + antihorario en los extremos
Deflexión )(
2
0
AB xL
EI
xM
y −
−
=
EI
LM
y
8
2
0
MAX
−
= para
2
L
x =
Pendiente )2(
2
0
AB xL
EI
M
−
−
=θ
EI
LM
2
0
BA
−
=−= θθ
Momento 0AB MM =
Cortante 0AB =V
Reacciones 0BA == RR
Viga en voladizo - Carga uniforme en todo el vano
Deflexión )64(
24
22340
AB xLLxx
EI
w
y +−
−
=
EI
Lw
yy
8
4
0
BMAX
−
== para x = L
Pendiente )33(
6
2230
AB xLLxx
EI
w
+−
−
=θ
EI
Lw
6
3
0
B
−
=θ
Momento 20
AB )(
2
xL
w
M −
−
=
2
2
0
AMAX
Lw
MM
−
==
Cortante )(0AB xLwV −=
Reacciones LwR 0A =
Viga en voladizo - Carga uniforme parcial en el lado empotrado
Deflexión )46(
24
43220
AC xaxxa
EI
w
y +−
−
=
)4(
24
3
0
CB ax
EI
aw
y −
−
=
)4(
24
3
0
BMAX aL
EI
aw
yy −
−
==
Pendiente )33(
6
3220
AC xaxxa
EI
w
+−
−
=θ
EI
aw
6
3
0
BCCB
−
=== θθθ
Momento 20
AC )(
2
xa
w
M −
−
= 0BCCB === MMM
2
2
0
AMAX
aw
MM
−
==
Cortante )(0AC xawV −= 0BCCB === VVV
Reacciones awR 0A =

11. Viga en voladizo - Carga uniforme parcial en el lado libre
Deflexión )233(
12
2
0
AC xaL
EI
bxw
y −+
−
=
)464(
24
4322340
CB axaxLLxx
EI
w
y +−+−
−
=
Pendiente )(
2
0
AC xaL
EI
bxw
−+
−
=θ
)33(
6
32230
CB axLLxx
EI
w
−+−
−
=θ
)(
6
330
B aL
EI
w
−
−
=θ
Momento )2(
2
0
AC xaL
bw
M −+
−
= 20
CB )(
2
xL
w
M −
−
=
Cortante bwVVV 0CAAC === )(0CB xLwV −=
Reacciones bwR 0A =
Viga en voladizo - Carga uniforme parcial
Deflexión )236(
12
2
0
AC xba
EI
bxw
y −+
−
=
)4)(6)(4(
24
4322340
CD axaxbaxbax
EI
w
y +−+++−
−
=
))(])([4(
24
44330
DB abaabax
EI
w
y ++−−+
−
=
Pendiente )2(
2
0
AC xba
EI
bxw
−+
−
=θ
))(3)(3(
6
32230
CD axbaxbax
EI
w
−+++−
−
=θ
))((
6
330
DB aba
EI
w
−+
−
=θ
Momento )22(
2
0
AC xba
bw
M −+
−
=
20
CD )(
2
xba
w
M −+
−
= 0BDDB === MMM
Cortante bwVVV 0CAAC === )(0CD xbawV −+=
0BDDB === VVV
Reacciones bwR 0A =

12. Viga en voladizo - Carga uniformemente creciente hacia el lado libre en todo el vano
Deflexión )1020(
120
323
2
0
AB xxLL
LEI
xw
y +−
−
=
EI
Lw
y
120
11 4
0
MAX
−
= para x = L
Pendiente )68(
24
3230
AB xxLL
LEI
xw
+−
−
=θ
EI
Lw
8
3
0
B
−
=θ
Momento )32(
6
3230
AB xxLL
L
w
M +−
−
=
Cortante )(
2
220
AB xL
L
w
V −=
Reacciones
2
0
A
Lw
R =
Viga en voladizo - Carga uniformemente creciente hacia el lado empotrado en todo el vano
Deflexión )51010(
120
3223
2
0
AB xLxxLL
LEI
xw
y −+−
−
=
EI
Lw
y
30
4
0
MAX = para x=L
Pendiente )464(
24
32230
AB xLxxLL
LEI
xw
−+−
−
=θ
EI
Lw
24
3
0
B
−
=θ
Momento 30
AB )(
6
xL
L
w
M −
−
=
Cortante 20
AB )(
2
xL
L
w
V −=
Reacciones
2
0
A
Lw
R =

13. Viga en voladizo - Carga cosenoidalmente decreciente hacia el lado libre en todo el vano
Deflexión ⎟
⎠
⎞
⎜
⎝
⎛
−+−
−
= 332333
4
0
AB ππ348
2
π
cos48
π3
xLxL
L
x
L
EI
Lw
y
)24π(
3π
2 3
4
4
0
MAX −
−
=
EI
Lw
y para x = L
Pendiente ⎟
⎠
⎞
⎜
⎝
⎛
−−
−
=
L
x
LxLx
EI
Lw
2
π
sen8ππ2
π
2222
3
0
ABθ
)8π(
π
2
3
3
0
B −
−
=
EI
Lw
θ
Momento ⎟
⎠
⎞
⎜
⎝
⎛
−−
−
=
L
x
LxL
Lw
M
2
π
cos2ππ
π
2
2
0
AB
Cortante ⎟
⎠
⎞
⎜
⎝
⎛
−=
L
xLw
V
2
π
sen1
π
2 0
AB
Reacciones
π
2 0
A
Lw
R =
Viga en voladizo - Carga puntual en el extremo libre
Deflexión )3(
6
32
AB xLx
EI
P
y −
−
=
EI
PL
yy
3
3
BMAX
−
==
Pendiente )2(
2
2
AB xLx
EI
P
−
−
=θ
EI
PL
2
2
BMAX
−
==θθ
Momento )(AB xLPM −−= PLMM −== AMAX
Cortante PVVV === BAAB
Reacciones PR =A
Viga en voladizo - Carga puntual en cualquier punto
Deflexión )3(
6
32
AC xax
EI
P
y −
−
= )3(
6
2
CB ax
EI
Pa
y −
−
=
)3(
6
2
BMAX aL
EI
Pa
yy −
−
==
Pendiente )2(
2
2
AC xax
EI
P
−
−
=θ
EI
Pa
2
2
BCCB
−
=== θθθ
Momento )(AC xaPM −−= 0BCCB === MMM
PaMM −== AMAX
Cortante PVVV === CAAC 0BCCB === VVV
Reacciones PR =A

14. Viga en voladizo - Momento horario en el extremo libre
Deflexión
EI
xM
y
2
2
0
AB
−
=
EI
LM
y
2
2
0
MAX
−
= para x = L
Pendiente
EI
xM0
AB
−
=θ
Momento 0BAAB MMMM −===
Cortante 0BAAB === VVV
Reacciones 0A =R
Viga en voladizo - Momento horario en cualquier punto
Deflexión
EI
xM
y
2
2
0
AC
−
= )2(
2
0
CB ax
EI
aM
y −
−
=
)2(
2
0
MAX aL
EI
aM
y −
−
= para x = L
Pendiente
EI
xM0
AC
−
=θ
EI
aM0
BCCB
−
=== θθθ
Momento 0AAC MMM −== 0BCB == MM
Cortante 0CAAC === VVV 0BCCB === VVV
Reacciones 0A =R
Viga empotrada - Carga uniforme en todo el vano
Deflexión 2
2
0
AB )(
24
xL
EI
xw
y −
−
=
Pendiente )23(
12
220
AB xLxL
EI
xw
+−
−
=θ
Momento )66(
12
220
AB xLxL
w
M +−
−
=
Cortante )2(
2
0
AB xL
w
V −=
Reacciones
2
0
BA
Lw
RR ==

15. Viga empotrada - Carga uniforme en la mitad del vano
Deflexión )124(
24
AA
2
0
2
AC MxRxw
EI
x
y −−
−
=
EI
LxLRMLRML
EI
xRxLRM
y
6
)2(3)3(
6
)(3
BBBB
2
3
B
2
BB
CB
+−+
+
+
−+
=
Pendiente )63(
6
AA
2
0AC MxRxw
EI
x
−−
−
=θ
[ ])2()(2
2
1
BBBB
2
BCB LRMLxLRMxR
EI
+++−
−
=θ
Momento
2
2
0
AAAC
xw
MxRM −+= BBCB )( MxLRM +−=
Cortante xwRV 0AAC −= BCB RV −=
Reacciones
L
MMLw
R BA0
A
8
3 −
−=
L
MMLw
R BA0
B
8
−
+=
Siendo
192
11 2
0
A
Lw
M
−
=
192
5 2
0
B
Lw
M
−
=
Viga empotrada - Carga uniforme parcial en un lado
Deflexión )124(
24
AA
2
0
2
AC MxRxw
EI
x
y −−
−
=
EI
LxLRMLRML
EI
xRxLRM
y
6
)2(3)3(
6
)(3
BBBB
2
3
B
2
BB
CB
+−+
+
+
−+
=
Pendiente )63(
6
AA
2
0AC MxRxw
EI
x
−−
−
=θ
[ ])2()(2
2
1
BBBB
2
BCB LRMLxLRMxR
EI
+++−
−
=θ
Momento
2
2
0
AAAC
xw
MxRM −+= BBCB )( MxLRM +−=
Cortante xwRV 0AAC −= BCB RV −=
Reacciones
L
MM
L
abLw
R BA0
A
2
)( −
−
+
=
L
MM
L
aw
R BA
2
0
B
2
−
+=
Siendo )386(
12
22
2
2
0
A aLaL
L
aw
M +−
−
=
)34(
12 2
3
0
B aL
L
aw
M −
−
=

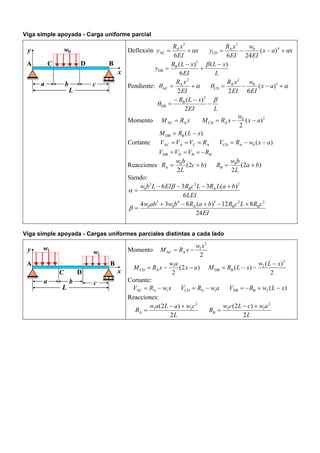
16. Viga empotrada - Carga uniforme parcial
Deflexión )3(
6
AA
2
AC xRM
EI
x
y +=
[ ]2
A
3
A
4
0CD 124)(
24
1
xMxRaxw
EI
y −−−
−
=
EI
LxLRMLRML
EI
xRxLRM
y
6
)2(3)3(
6
)(3
BBBB
2
3
B
2
BB
DB
+−+
+
+
−+
=
Pendiente )2(
2
AAAC xRM
EI
x
+=θ
[ ]xMxRaxw
EI
A
2
A
3
0CD 63)(
6
1
−−−
−
=θ
[ ])2()(2
2
1
BBBB
2
BDB LRMLxLRMxR
EI
+++−
−
=θ
Momento xRMM AAAC +=
2
)( 2
0
AACD
axw
MxRM
−
−+=
)(BBDB xLRMM −+=
Cortante AAC RV = )(0ACD axwRV −−= BDB RV −=
Reacciones
L
MMbbcw
R
2
22)2( BA0
A
+−+
=
L
MMbbaw
R
2
22)2( BA0
B
−++
=
Siendo [ ]22
2
0
A )2)(36()362(
24
bcbabcLb
L
bw
M +++−−
−
=
[ ]22
2
0
B )2)(36()362(
24
babcbaLb
L
bw
M +++−−
−
=
Viga empotrada - Carga puntual en el centro
Deflexión )43(
48
2
AC xL
EI
Px
y −
−
= )4(
48
)( 2
CB Lx
EI
xLP
y −
−−
=
Pendiente )2(
8
AC xL
EI
Px
−
−
=θ )23(
8
22
CB xLxL
EI
P
+−
−
=θ
Momento )4(
8
AC xL
P
M −
−
= )43(
8
CB xL
P
M −=
Cortante
2
AC
P
V =
2
CB
P
V
−
=
Reacciones
2
BA
P
RR ==

17. Viga empotrada - Carga puntual en cualquier punto
Deflexión )33(
6 3
22
AC bxaxaL
EIL
xPb
y −−
−
=
)3(
6
)(
3
22
CB axaLbx
EIL
xLPa
y +−
−−
=
Pendiente )32(
2 3
2
AC bxaxaL
EIL
xPb
−−
−
=θ
[ ]2
3
2
CB )3(
2
)(
Labx
EIL
xLPa
−+
−
=θ
Momento )3(3
2
AC bxaxaL
L
xPb
M −−
−
=
)2( 2
3
2
CB bxLxbLL
L
Pa
M −−+=
Cortante )2(3
2
AC aL
L
Pb
V += )2(3
2
CB bL
L
Pa
V +
−
=
Reacciones )2(3
2
A aL
L
Pb
R += )2(3
2
B bL
L
Pa
R +=
Viga empotrada - Dos cargas puntuales iguales situadas simétricamente
Deflexión )33(
6
2
2
AC LxaaL
EIL
Px
y −−
−
=
)33(
6
2
2
CD aLxLx
EIL
Pa
y −−
−
=
))(33(
6
)( 2
2
DB xLLaaL
EIL
xLP
y −−−
−−
=
Pendiente )22(
2
2
AC LxaaL
EIL
Px
−−
−
=θ )2(
2
2
CD xL
EIL
Pa
−
−
=θ
[ ])(22
2
)( 2
DB xLLaaL
EIL
xLP
−−−
−
=θ
Momento )( 2
AC aaLLx
L
P
M +−=
L
Pa
M
2
CD = )( 22
DB aLaLxL
L
P
M +−−=
Cortante PV =AC 0CD =V PV −=DB
Reacciones PRR == BA

18. Viga empotrada - Momento antihorario en el centro
Deflexión )2(
8
2
0
AC Lx
LEI
xM
y −=
)425(
8
32320
CB LxLxLx
LEI
M
y +−−
−
=
Pendiente )3(
4
0
AC Lx
LEI
xM
−=θ )4610(
8
220
CB LxLx
LEI
M
−−
−
=θ
Momento )6(
4
0
AC Lx
L
M
M −= )65(
4
0
CB xL
L
M
M −
−
=
Cortante
L
M
V
2
3 0
AB =
Reacciones
L
M
R
2
3 0
A =
L
M
R
2
3 0
B
−
=
Viga empotrada - Momento antihorario en cualquier punto
Deflexión:
)22(
2 3
2
0
AC bLaxaL
EIL
bxM
y −−
−
= )2(
2
)(
3
2
0
CB aLbx
EIL
xLaM
y −
−
=
Pendiente:
)32(3
0
AC bLaxaL
EIL
bxM
−−
−
=θ )3(
)( 2
3
0
CB bxL
EIL
xLaM
−
−
=θ
Momento:
)62(3
0
AC bLaxaL
L
bM
M −−
−
= )46(3
0
CB aLbLbx
L
aM
M −−=
Cortante 3
0
AB
6
L
abM
V =
Reacciones 3
0
A
6
L
abM
R = 3
0
B
6
L
abM
R
−
=
Siendo )2(2
0
A ba
L
bM
M −
−
= )2(2
0
B ab
L
aM
M −=
Viga empotrada / apoyada - Carga uniforme en todo el vano
Deflexión )253(
48
22
2
0
AB xLxL
EI
xw
y +−
−
=
Pendiente )8156(
48
220
AB xLxL
EI
xw
+−
−
=θ
Momento )45(
8
220
AB xLxL
w
M +−
−
=
Cortante )85(
8
0
AB xL
w
V −=
Reacciones
8
5 0
A
Lw
R =
8
3 0
B
Lw
R =

19. Viga empotrada / apoyada - Carga uniforme parcial en el lado empotrado
Deflexión:
EIL
bLxLawxaLwxLLR
y
48
)3)(()(2)(8 3
0
4
0
3
B
AC
+−−−−−
=
EIL
bLxLawxLLR
y
48
)3)(()(8 3
0
3
B
CB
+−−−
=
Pendiente:
EIL
bLawxaLwxLLR
48
)3()(8)(24 3
0
3
0
2
B
AC
++−+−−
=θ
EIL
bLawxLLR
48
)3()(24 3
0
2
B
CB
++−−
=θ
Momento
2
)()(2 2
0B
AC
xawxLR
M
−−−
= )(BCB xLRM −=
Cortante )(0BAC xawRV −+−= BCB RV −=
Reacciones
L
MabLw
R
2
2)( A0
A
−+
=
L
Maw
R
2
2 A
2
0
B
+
=
Siendo 2
22
0
A
8
)(
L
abLw
M
+−
=
Viga empotrada / apoyada - Carga uniforme parcial en el lado apoyado
Deflexión )3(
6
AA
2
AC MxR
EI
x
y +=
EIL
aabbLxLbw
EIL
xLLwxLLR
y
48
)63)((
24
)()(4
22
0
4
0
3
B
CB
++−−
+
+
−−−
=
Pendiente )2(
2
AAAC MxR
EI
x
+=θ
EIL
aabbLbw
EIL
xLLwxLLR
48
)63(
6
)()(3 22
0
3
0
2
B
CB
++
+
−+−−
=θ
Momento AAAC MxRM +=
2
)()(2 2
0B
CB
xLwxLR
M
−−−
=
Cortante AAC RV = )(0BCB xLwRV −+−=
Reacciones
L
Mbw
R
2
2 A
2
0
A
−
=
L
Mbbaw
R
2
2)2( A0
B
++
=
Siendo [ ]2
2
2
0
A ))(2(
16
baLbL
L
bw
M −++
−
=

20. Viga empotrada / apoyada - Carga uniforme parcial
Deflexión )3(
6
AA
2
AC MxR
EI
x
y +=
[ ]
EIL
babcbabLbxLbw
EI
cxLwxLR
y
96
)2)(2(3)2(32)(
24
)()(4
222
0
4
0
3
B
CD
++++−−−
+
+
−−−−
=
[ ]
EIL
babcbabLbxLbw
EI
xLR
y
96
)2)(2(3)2(32)(
6
)(
222
0
3
B
DB
++++−−−
+
+
−
=
Pendiente )2(
2
AAAC MxR
EI
x
+=θ
[ ]
EIL
babcbabLbbw
EI
cxLwxLR
96
)2)(2(3)2(32
6
)()(3
222
0
3
0
2
B
CD
++++−
+
+
−−+−−
=θ
[ ]
EIL
babcbabLbbw
EI
xLR
96
)2)(2(3)2(32
2
)(
222
0
2
B
DB
++++−
+
+
−−
=θ
Momento AAAC MxRM +=
2
)()(2 2
0B
CD
cxLwxLR
M
−−−−
= )(BDB xLRM −=
Cortante AAC RV = B0CD )( RcxLwV −−−= BDB RV −=
Reacciones
L
Mbcbw
R
2
2)2( A0
A
−+
=
L
Mbbaw
R
2
2)2( A0
B
++
=
Siendo
[ ]
2
2
0
A
16
)2)(22()2)(2(
L
bbabcLbbabcw
M
−+++++−
=

21. Viga empotrada / apoyada - Carga puntual en el centro
Deflexión:
)119(
96
2
AC xL
EI
Px
y −
−
= ))(53(
96
)( 22
CB xLL
EI
xLP
y −−
−−
=
Pendiente:
)116(
32
AC xL
EI
Px
−
−
=θ )5104(
32
22
CB xLxL
EI
P
+−
−
=θ
Momento )113(
16
AC xL
P
M −
−
= )(
16
5
CB xL
P
M −=
Cortante
16
11
AC
P
V =
16
5
CB
P
V
−
=
Reacciones
16
11
A
P
R =
16
5
B
P
R =
Viga empotrada / apoyada - Carga puntual en cualquier punto
Deflexión )333(
12
2223
3
2
AC xbxLLbL
EIL
Pbx
y +−−
−
=
)))(2(3(
12
)( 22
3
2
CB xLbLbL
EIL
xLPa
y −+−
−−
=
Pendiente )322(
4
2223
3AC xbxLLbL
EIL
Pbx
+−−
−
=θ
)2242(
4
2223
3
2
CB bxLxbLxxLL
EIL
Pa
++−−
−
=θ
Momento:
)3(
2
2223
3AC xbxLLbL
L
Pb
M +−−
−
= )2)((
2 3
2
CB bLxL
L
Pa
M +−=
Cortante )3(
2
22
3AC bL
L
Pb
V −= )2(
2 3
2
CB bL
L
Pa
V +
−
=
Reacciones )3(
2
22
3A bL
L
Pb
R −= )2(
2 3
2
B bL
L
Pa
R +=

22. Viga empotrada / apoyada - Dos cargas puntuales iguales situadas simétricamente
Deflexión:
[ ])33(2))(233(
12
2222
2
2
AC LaLaLxLLaLa
EIL
Px
y +−+−−−=
[ ]
2
222
2
223
CD
12
2))((3
12
))(6))((3(
EIL
aLxLaLLPa
EIL
xLLxLaLPa
y
−−+−
+
+
−−−−−
=
[ ])(3))(233(
12
)( 2222
2DB aLaLxLLaaL
EIL
xLP
y −+−−−
−−
=
Pendiente:
[ ])33(4)32)(233(
12
2222
2AC LaLaLxLLaLa
EIL
Px
+−+−−−=θ
[ ])()(4))((3
4
222
2CD aLLxLLxLaL
EIL
Pa
+−−+−−−
−
=θ
[ ])())(233(
4
2222
2DB aLaLxLLaaL
EIL
P
−+−−−=θ
Momento [ ])332(33
2
2222
2AC aaLLxaLLa
L
P
M −++−=
[ ]2
2CD 2))((3
2
LxLaL
L
Pa
M −−−
−
=
)233(
2
)( 22
2DB LaaL
L
xLP
M −−
−−
=
Cortante )332(
2
22
2AC aaLL
L
P
V −+= 2CD
2
)(3
L
aLPa
V
−
=
)233(
2
22
2DB LaaL
L
P
V −−=
Reacciones )332(
2
22
2A aaLL
L
P
R −+=
)323(
2
22
2B aLLa
L
P
R −+=

23. Viga empotrada / apoyada - Momento horario en cualquier punto
Deflexión: [ ]))((2
4
222
3
2
0
AC bLxLLb
EIL
xM
y −−−
−
=
[ ]))(3)((4
4
)( 223
3
0
CB bLLxLL
EIL
xLaM
y +−−−−
−−
=
Pendiente [ ]))(32(4
4
222
3
0
AC bLxLLb
EIL
xM
−−−
−
=θ
[ ])2)((34
4
23
3
0
CB LxxbLL
EIL
aM
−+−
−
=θ
Momento [ ]))(3(2
2
222
3
0
AC bLxLLb
L
M
M −−−
−
=
))((
2
3
3
0
CB xLbL
L
aM
M −+=
Cortante )(
2
3
3
0
AB bL
L
aM
V +
−
=
Reacciones )(
2
3
3
0
A bL
L
aM
R +
−
= )(
2
3
3
0
B bL
L
aM
R +=
Viga empotrada / apoyada - Momento horario en el lado apoyado
Deflexión
EIL
xLxM
y
4
)(2
0
AB
−
=
Pendiente
EIL
xLxM
4
)32(0
AB
−
=θ
Momento
L
xLM
M
2
)3(0
AB
−
=
Cortante
L
M
V
2
3 0
AB
−
=
Reacciones
L
M
R
2
3 0
A
−
=
L
M
R
2
3 0
B =

24. Viga con vano lateral - Carga uniforme en todo el vano
Deflexión )222(
24
222232240
AB xaLaLxxLL
LEI
xw
y +−+−
−
=
)464(
24
3
1
2
11
23210
BC xaxxaLLa
EI
xw
y +−+−
−
=
Pendiente )6246(
24
222232240
AB xaLaLxxLL
LEI
w
+−+−
−
=θ
)412124(
24
3
1
2
11
2320
BC xaxxaLLa
EI
w
+−+−
−
=θ
Momento )(
2
220
AB aLxL
L
xw
M −−= 2
1
0
BC )(
2
xa
w
M −
−
=
Cortante )2(
2
220
AB aLxL
L
w
V −−= )( 10BC xawV −=
Reacciones )(
2
220
A aL
L
w
R −= 20
B )(
2
aL
L
w
R +=
Siendo Lxx −=1
Viga con vano lateral - Carga uniforme sobre el saliente
Deflexión )(
12
22
2
0
AB xL
LEI
xaw
y −=
)464(
24
3
1
2
11
2210
BC xaxxaLa
EI
xw
y +−+
−
=
Pendiente )3(
12
22
2
0
AB xL
LEI
aw
−=θ
)33(
6
3
1
2
11
220
BC xaxxaLa
EI
w
+−+
−
=θ
Momento
L
xaw
M
2
2
0
AB
−
= 2
1
0
BC )(
2
xa
w
M −
−
=
Cortante
L
aw
V
2
2
0
AB
−
= )( 10BC xawV −=
Reacciones
L
aw
R
2
2
0
A
−
=
L
aaLw
R
2
)2(0
B
+
=
Siendo Lxx −=1

25. Viga con vano lateral - Carga puntual en el extremo saliente
Deflexión )(
6
22
AB xL
LEI
Pax
y −= )32(
6
2
11
1
BC xaxaL
EI
Px
y −+
−
=
Pendiente )3(
6
22
AB xL
LEI
Pa
−=θ )362(
6
2
11BC xaxaL
EI
P
−+
−
=θ
Momento
L
Pax
M
−
=AB )( 1BC xaPM −−=
Cortante
L
Pa
V
−
=AB PV =BC
Reacciones
L
Pa
R
−
=A
L
aLP
R
)(
B
+
=
Siendo Lxx −=1
Viga con vano lateral - Carga puntual entre los apoyos
Deflexión )(
6
222
AC xbL
LEI
Pbx
y −−
−
=
)2(
6
)( 22
CB xaLx
LEI
xLPa
y −−
−−
=
)(
6
1
BD aL
LEI
Pabx
y +=
Pendiente )3(
6
222
AC xbL
LEI
Pb
−−
−
=θ
)362(
6
222
CB xaLxL
LEI
Pa
++−
−
=θ
LEI
aLPab
6
)(
BD
+
=θ
Momento
L
Pbx
M =AC )(CB xL
L
Pa
M −= 0BD =M
Cortante
L
Pb
V =AC
L
Pa
V
−
=CB 0BD =V
Reacciones
L
Pb
R =A
L
Pa
R =B
Siendo Lxx −=1
www.vaxasoftware.com