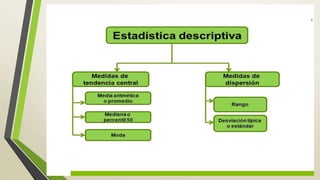
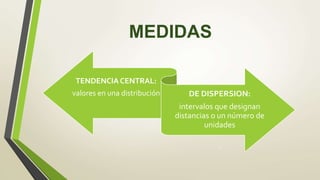
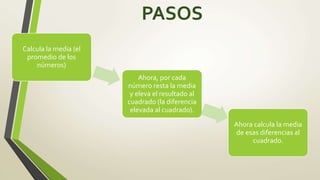
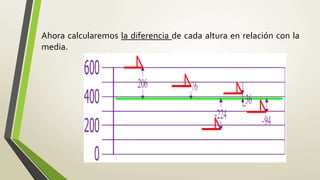
Este documento proporciona una introducción a las medidas estadísticas descriptivas de tendencia central, dispersión y desviación. Explica que la desviación estándar y la varianza miden cuánto se separan los datos de la media, y que la desviación estándar se calcula como la raíz cuadrada de la varianza. Además, proporciona un ejemplo numérico para calcular la media, varianza y desviación estándar de un conjunto de datos de alturas de perros.

1. ESTADISTICA DESCRIPTIVA
PROFESOR: Dra. María Isabel Rosales Rosales
ALUMNO: Flor M. Chávez Aguayo
MAYO 2018

3. MEDIDAS
TENDENCIA CENTRAL:
valores en una distribución DE DISPERSION:
intervalos que designan
distancias o un número de
unidades
:

4. MEDIDAS DE DESVIACIÓN
Las medidas de la variabilidad indican la dispersión de los datos en
la escala de medición y responden a la pregunta:
¿dónde están diseminadas las puntuaciones o los valores obtenidos?
En la escala de medición, las medidas de la variabilidad más utilizadas
son:
RANGO DESVIACION VARIANZA

5. EL RANGO
• El rango, también llamado recorrido, es la diferencia entre la
puntuación mayor y la puntuación menor, e indica el número de
unidades en la escala de medición que se necesitan para incluir
los valores máximo y mínimo.

6. EL RANGO
Se calcula así:
• XM – Xm (puntuación mayor, menos puntuación menor).
Si tenemos los siguientes valores:
17 18 20 20 24 28 28 30 33
El rango será: 33 – 17 = 16.
Cuanto más grande sea el rango, mayor será la dispersión de los
datos de una distribución.

7. LA DESVIACIÓN ESTÁNDAR O
TÍPICA
• Es el promedio de desviación de las puntuaciones con respecto a la media.
• Esta medida se expresa en las unidades originales de medición de la
distribución.
• Se interpreta en relación con la media.

8. DESVIACION ESTANDAR
Cuanto mayor sea la dispersión de los datos alrededor de la media, mayor será
la desviación estándar.
Se interpreta como:
Cuánto se desvía, en promedio, de la media un conjunto de puntuaciones.
Supongamos que un investigador obtuvo para su muestra una media
(promedio) de ingreso familiar anual de $6 000 y una desviación estándar de
$1 000.
La interpretación es que los ingresos familiares de la muestra se desvían, en
promedio, mil unidades monetarias respecto a la media.
• La desviación estándar sólo se utiliza en variables medidas por intervalos o de
razón

9. LAVARIANZA
La varianza es la desviación estándar elevada al cuadrado y se
simboliza s2.
Es un concepto estadístico muy importante, ya que muchas de las
pruebas cuantitativas se fundamentan en él.
Diversos métodos estadísticos parten de la descomposición de la
varianza; sin embargo, con fines descriptivos se utiliza
preferentemente la desviación estándar.

10. EN RESUMEN:
• Desviación Estándar: significa que tan lejos esta de lo normal.
• Desviación estándar (σ) mide cuánto se separan los datos.
• La fórmula es fácil: es la raíz cuadrada de la varianza.
• La varianza (que es el cuadrado de la desviación estándar: σ2)
Se define así: Es la media de las diferencias con la media elevadas
al cuadrado.

11. PASOS
Calcula la media (el
promedio de los
números)
Ahora, por cada
número resta la media
y eleva el resultado al
cuadrado (la diferencia
elevada al cuadrado).
Ahora calcula la media
de esas diferencias al
cuadrado.

12. EJEMPLO
Calcular: la media, la varianza y la desviación estándar.
Nosotras medimos las alturas de nuestros perros (en milímetros) La
alturas (de los hombros) son:
600mm, 470mm, 170mm, 430mm y 300mm.

13. MEDIA
Media =
600 + 470 + 170 + 430 + 300 = 1970 = 394
5

14. Ahora calcularemos la diferencia de cada altura en relación con la
media.

16. .
¿POR QUÉ AL CUADRADO?
• Elevar cada diferencia al cuadrado hace que todos los números sean
positivos (para evitar que los números negativos reduzcan la
varianza) y también hacen que las diferencias grandes se destaquen.
Por ejemplo 1002=10,000 es mucho más grande que 502=2,500. Pero
elevarlas al cuadrado hace que la respuesta sea muy grande, así que lo
deshacemos (con la raíz cuadrada) y así la desviación estándar es
mucho más útil.

17. ¿DUDAS, COMENTARIOS?

18. MUCHAS GRACIAS POR SU
ATENCION