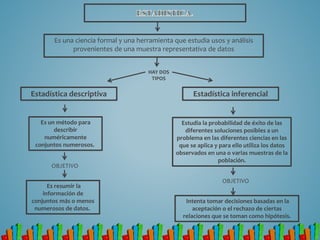
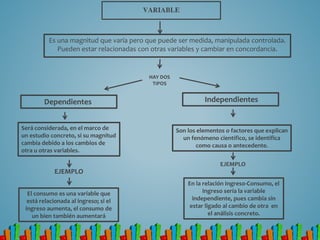
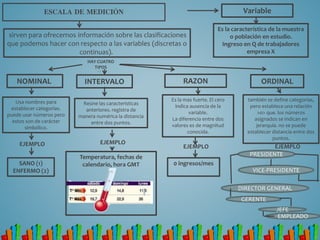
La estadística es una ciencia que estudia la recolección, análisis y presentación de datos. Existen dos tipos principales: estadística descriptiva, que resume conjuntos de datos, y estadística inferencial, que estudia la probabilidad de éxito de soluciones a problemas usando muestras de datos. Las variables, muestras, parámetros estadísticos y escalas de medición son conceptos fundamentales en estadística para describir y analizar datos.

1. ESTADÍSTICA
I
Alumna: Audelis Rincones
C.I: 26,256,448.Profesor: Ramón Aray
Seccion: YV

2. Es una ciencia formal y una herramienta que estudia usos y análisis
provenientes de una muestra representativa de datos
HAY DOS
TIPOS
Estadística descriptiva
Es un método para
describir
numéricamente
conjuntos numerosos.
OBJETIVO
Es resumir la
información de
conjuntos más o menos
numerosos de datos.
Estadística inferencial
Estudia la probabilidad de éxito de las
diferentes soluciones posibles a un
problema en las diferentes ciencias en las
que se aplica y para ello utiliza los datos
observados en una o varias muestras de la
población.
OBJETIVO
Intenta tomar decisiones basadas en la
aceptación o el rechazo de ciertas
relaciones que se toman como hipótesis.

3. VARIABLE
Es una magnitud que varía pero que puede ser medida, manipulada controlada.
Pueden estar relacionadas con otras variables y cambiar en concordancia.
HAY DOS
TIPOS
Dependientes
Será considerada, en el marco de
un estudio concreto, si su magnitud
cambia debido a los cambios de
otra u otras variables.
Independientes
Son los elementos o factores que explican
un fenómeno científico, se identifica
como causa o antecedente.
EJEMPLO
El consumo es una variable que
está relacionada al ingreso; si el
ingreso aumenta, el consumo de
un bien también aumentará
EJEMPLO
En la relación Ingreso-Consumo, el
Ingreso sería la variable
independiente, pues cambia sin
estar ligado al cambio de otra en
el análisis concreto.

4. En algunos casos se trabaja con toda una
población que es el conjunto formado por
todos los elementos a estudiar, el cual
puede llamarse conjunto completo.
EJEMPLO
• Comerciantes, esta es la forma en que se define a las
personas que dedican su vida al comercio
• La gente que habita en el campo de un país
representa su población rural.
• La población con deficiencia económica o cultural,
esta se puede ver en barrios bajos, guetos, favelas etc.
• La población de adultos mayores en la Comunidad
Europea.
• La población de Aves en peligro de extinción de la
selva del Amazonas.
• La población de bacterias E colli que se encuentra en
un cultivo de agar.
EJEMPLO
Supongamos que debemos estudiar la
altura de los niños que cumplen 10 años en
el presente año. Nos damos cuenta que no
podemos hacerlo con todos los cientos de
miles de niños que cumplen 10 años en el
país, lo que sería toda la población o
conjunto completo. Podemos hacerlo con
un grupo que sea manejable. O sea que
vamos a usar una muestra. Queremos que
esa muestra sea una buena representación
de todo el conjunto.
En estadísticas, una muestra es un
subconjunto de casos o individuos de
una población estadística.

5. PARAMETROS ESTADISTICOS
Es un número que se obtiene a partir de los datos de una distribución estadística.
Sirven para sintetizar la información dada por una tabla o por una gráfica.
HAY TRES
TIPOS
CENTRALIZACIÓN
Será considerada, en el marco de un
estudio concreto, si su magnitud
cambia debido a los cambios de otra u
otras variables. Nos indican en torno a
que valor, se distribuyen los datos
EJEMPLO
Ejemplo : Salarios de las 11 personas de
una empresa.
POSICION
Las medidas de posición dividen
un conjunto de datos en grupos
con el mismo número de
individuos.
EJEMPLO
El 5% de los recién nacidos tienen
un peso demasiado bajo. ¿Qué
peso se considera “demasiado
bajo”?
R: percentil 5 o cuantil 0,05
DISPERSION
Las medidas de dispersión nos
informan sobre cuanto se alejan
del centro los valores de la
distribución.
EJEMPLO
Si la medida es 80 y la desviación
típica de 20 entonces
CV=20/80=0,25=25%
Frecuencia nª: sueldos
2
3
1
2
2
1
50,000ptsmes70,000
75,000 85,000
90,000 1,000,00
Salario: medio de :
157,727 pts/mes

6. ESCALA DE MEDICIÓN
sirven para ofrecernos información sobre las clasificaciones
que podemos hacer con respecto a las variables (discretas o
continuas).
HAY CUATRO
TIPOS
NOMINAL
Usa nombres para
establecer categorías.
puede usar números pero
estos son de carácter
simbólico.
EJEMPLO
SANO (1)
ENFERMO (2)
ORDINAL
también se define categorías,
pero establece una relación
>o> que. los números
asignados se indican en
jerarquía. no se puede
establecer distancia entre dos
puntos.
EJEMPLO
Reúne las características
anteriores. registra de
manera numérica la distancia
entre dos puntos.
Variable
Es la característica de la muestra
o población en estudio.
Ingreso en Q de trabajadores
empresa X
EJEMPLO
INTERVALO RAZON
PRESIDENTE
GERENTE
VICE-PRESIDENTE
JEFE
DIRECTOR GENERAL
EMPLEADO
Temperatura, fechas de
calendario, hora GMT
Es la mas fuerte. El cero
indica ausencia de la
variable.
La diferencia entre dos
valores es de magnitud
conocida.
EJEMPLO
0 ingresos/mes

7. SUMATORIA
La sumatoria o
sumatorio se emplea
para representar la
suma de muchos o
infinitos sumandos.
La expresión se lee: “sumatoria de
Xi, donde i toma los valores de 1 a n“.
La operación sumatoria se expresa
con la letra griega sigma
mayúscula Σ.
i es el valor inicial llamado límite
inferior.
n es el valor final llamado límite
superior.
EJEMPLO
En un test realizado a un grupo
de 42 personas se han obtenido las
puntuaciones que muestra la
tabla. Calcula la media.
Es el cociente entre dos
números, en el que ninguno o
sólo algunos elementos del
numerador están incluidos en el
denominador. El rango es de 0 a
infinito.
TEST
Razón casos de legionelosis en
Andalucía/casos de legionelosis
en Canarias: 83/11= 7,55. Por cada
caso de legionelosis declarado en
Canarias hay 7,55 casos
declarados en Andalucía.
xi fi
xi ·
fi
[10,
20)
15 1 15
[20,
30)
25 8 200
[30,
40)
35 10 350
[40,
50)
45 9 405
[50,
60
55 8 440
[60,
70)
65 4 260
[70,
80)
75 2 150
Σxi =
42
Σxi ·
fi =
1
820
RAZON
EJEMPLO

8. PROPORCIÓN
Es una razón en la cual los
elementos del numerador
están incluidos en el
denominador. Se utiliza como
estimación de la probabilidad
de un evento. El rango es de
0 a 1 (o de 0 a 100%).
Casos de legionelosis en
Andalucía en relación al total
de casos en España: 83/1295=
0,064. El 6,4% de los casos de
legionelosis en España se
declararon en Andalucía.
EJEMPLO
Es un tipo especial de razón o
de proporción que incluye una
medida de tiempo en el
denominador. Está asociado
con la rapidez de cambio de un
fenómeno por unidad de una
variable (tiempo, temperatura,
presión).
son el numerador, el
denominador, el tiempo
específico en el que el hecho
ocurre, y usualmente un
multiplicador, potencia de 10, que
convierte una fracción o decimal
en un número entero. El rango es
de 0 a infinito.
FRECUENCIA
COMPONENTES
TASA
La tasa de legionelosis en Andalucía en
el año 2005: 83/7.849.799= 1,06*10-5. 1,06
personas por cada 100.000 habitantes,
padecieron legionelosis en Andalucía.
EJEMPLO
En un evento x, es el número de
veces ni que dicho evento se
repite durante un experimento
o muestra
estadística.1 Comúnmente, la
distribución de la frecuencia
suele visualizarse con el uso de
histograma.
Supongamos que
las calificaciones de un estudiante
de secundaria fueran las siguientes:
18, 13, 12, 14, 11, 08, 12, 15, 05, 20, 18,
14, 15, 11, 10, 10, 11, 13.
Entonces:
La frecuencia absoluta de 11 es 3,
pues 11 aparece 3 veces.
EJEMPLO

9. BIBLIOGRAFÍA
• es.wikipedia.org/wiki/
• www.Estadisticaparaadministracion.blogs
• www.es.slideshare.net
• www.buenastareas.com
• www.uv.es
• es.slideshare.net