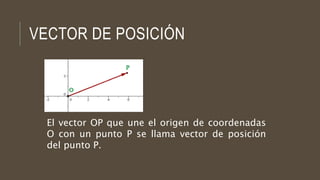
Este documento trata sobre vectores cartesianos y sus componentes. Explica que una fuerza puede descomponerse en dos componentes perpendiculares llamadas Fx y Fy a lo largo de los ejes x e y, respectivamente. También introduce los vectores unitarios i y j, y explica que una fuerza F puede escribirse como la suma de sus componentes Fx y Fy multiplicadas por i y j. Además, cubre conceptos como ángulos directores, vectores de posición, producto escalar y las leyes de senos y cosenos.

1. ESTÁTICA * TAREA 3
Griselda Monserrat
Pérez Valadez
Reg. 16310310
1 B T/M

2. VECTORES CARTESIANOS
Existen casos donde es deseable fraccionar una fuerza en dos
componentes perpendiculares entre sí. La fuerza F es posible
descomponerla en una componente llamada Fx a lo largo del
eje x y en una componente llamada Fy a lo largo del eje y. La
figura que se dibuja para obtener las dos componentes Fx y Fy
es un rectángulo y por lo tanto Fx y Fy reciben el nombre de
componentes rectangulares o también vectores cartesianos.
Los ejes x y y se seleccionan generalmente en forma
horizontal y vertical de manera acorde al plano
de René Descartes. Al determinar las componentes
rectangulares de una fuerza se deben visualizar como
perpendiculares a estos ejes.

3. VECTORES UNITARIOS
Al momento de presentar dos vectores de magnitud
unitaria, dirigidos a lo largo de las direcciones
positivas de los ejes x y y. Estos vectores se
denominan vectores unitarios y se denotan como i y
j respectivamente.
Como el producto de un escalar y un vector, podemos
definirlo como las componentes rectangulares Fx y Fy
de una fuerza F multiplicada por los vectores unitarios
i y j, 7 entonces podemos escribir:
Fx = Fxi Fy = Fyj
Entonces F = Fxi + Fyj

4. ÁNGULOS DIRECTORES
Se llaman ÁNGULOS DIRECTORES de un vector, a los
ángulos que el vector forma con las direcciones
positivas de los ejes coordenados.
Estos ángulos deberán ser tomados entre 0 y π (0º y
180º).

5. VECTOR DE POSICIÓN
El vector OP que une el origen de coordenadas
O con un punto P se llama vector de posición
del punto P.

6. PRODUCTO ESCALAR
El producto escalar de dos vectores es un número real
que resulta al multiplicar el producto de sus módulos
por el coseno del ángulo que forman.

7. LEYES DE SENOS Y COSENOS
Ley de los senos: Los lados de un triángulo son
proporcionales a los senos de los ángulos opuestos:
El coseno (abreviado como cos) es la razón entre
el cateto adyacente y la hipotenusa.
Si usamos una circunferencia unitaria (con radio igual
a uno), entonces la hipotenusa, AB, del triángulo se
hace 1, por lo que las relaciones quedan
cos α = sen β = |AC| / |AB| = |AC| / 1 = |AC| = b

8. Ley de los cosenos: El cuadrado de un lado es igual
a la suma de los cuadrados de los otros lados menos
el doble del producto de estos lados por el coseno del
ángulo comprendido.
a^2 = b^2 + c^2 − 2bc * cos(A)
b^2 = a^2 + c^2 − 2ac * cos(B)
c^2 = a^2 + b^2 − 2ab * cos(C)