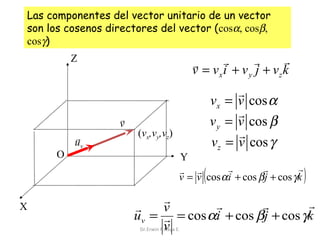
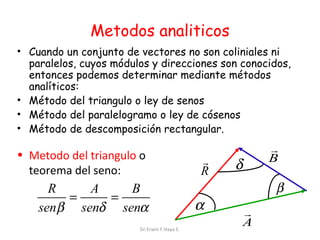
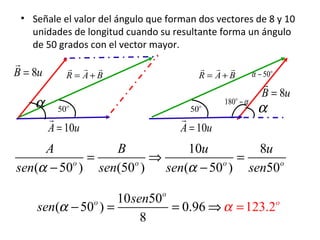
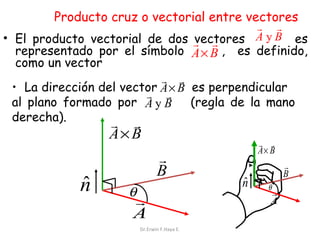
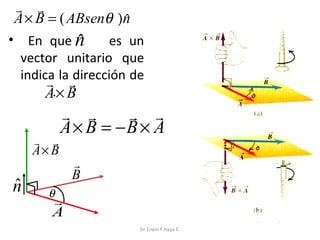
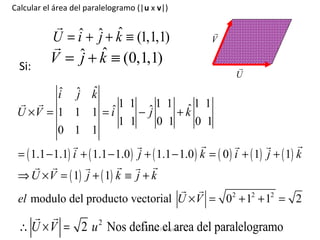
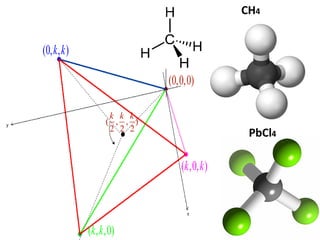
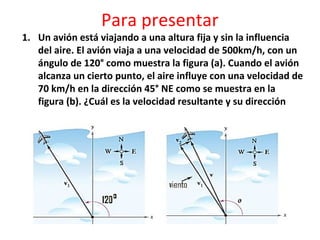
El documento describe las características de las cantidades físicas escalares y vectoriales. Las cantidades escalares se definen por un número real y una unidad, mientras que las cantidades vectoriales se definen por magnitud, dirección y sentido. Se explican conceptos como módulo, dirección, sentido y punto de aplicación para representar vectores. También se describen métodos para determinar la resultante de vectores concurrentes y no colineales.

4. Dr.Erwin F.Haya E.

5. Cantidades físicas
• Existen cantidades físicas que quedan totalmente
determinadas por su magnitud o tamaño, indicada en
alguna unidad conveniente.
Magnitud escalar:
• Son aquellas magnitudes físicas que estan definidas por
un numero real y su correspondiente unidad de medida.
Es decir queda totalmente definida mediante un escalar
Masa (10 g)
Tiempo (5 s)
Longitud (15 mm)
Temperatura (23 ºC)
Presión
densidad
corriente eléctrica
carga eléctrica
...
Dr.Erwin F.Haya E.

6. Ejemplos de Cantidades físicas
Magnitud vectorial:
Son aquellas magnitudes físicas que se manifiesta por tres
características fundamentales: Modulo, una dirección y un
sentido.

v

v



Velocidad (2i + 3 j + 1k )m / s

Fuerza (2k ) N
Momento de una
fuerza
Aceleración
Vector de posición
Cantidad de movimiento

F
...
Dr.Erwin F.Haya E.

a

7. Vector: segmento orientado en el espacio mediante
una flecha que permite representar una magnitud
vectorial
Sentido.— Nos indicando hacia
qué lado de la línea de acción se
dirige el vector
Dirección.— Es la recta sobre
la cual se encuentra la línea de
acción
Magnitud o Modulo.— Indica el
valor numérico o la longitud del
vector.
Origen o Punto de aplicación.—
Es el lugar concreto en donde
se comienza a dibujar el vector

8. MÓDULO
El MÓDULO viene dado por la longitud de la flecha. El módulo es
proporcional a la intensidad de la fuerza.
Al representar las fuerzas usaremos una escala similar a la
utilizada en los mapas, por ejemplo, 1 centímetro en el papel
equivaldrá a 1 Newton de fuerza (1 cm:1 N).
Escala Þ 1 cm : 2 N
3 cm
3 cm . 2 N
1 cm
= 6N

9. DIRECCIÓN
La DIRECCIÓN es la recta sobre la que se aplica la fuerza. Viene
expresada por el ángulo que forma la recta con la horizontal: 0º
(horizontal), 30º, 47º, 90º (vertical), 130º, 249º, etc.
120º
45º
- 30º = 330º
- 100º = 260º
!OJO! En el S.I. la unidad de ángulo es el RADIÁN:
2π rad = 360º; π rad = 180º; π/2 rad = 90º, etc.

10. SENTIDO
El SENTIDO indica hacia dónde se aplica la fuerza. En una misma
dirección existen dos sentidos posibles.
Sentido hacia arriba, hacia la
derecha o ascendente
45º
Sentido hacia abajo, hacia la
izquierda o descendente

11. PUNTO DE APLICACIÓN
El PUNTO DE APLICACIÓN es el punto del espacio en que se aplica
la fuerza. Esto es importante, pues los efectos que producen las
fuerzas dependen en muchos casos del punto de aplicación.

FLuna, Tierra

FTierra, Luna
FLuna, Tierra = FTierra, Luna
Ambas fuerzas tienen el mismo módulo, pero
difieren en su PUNTO DE APLICACIÓN.

12. ALGUNOS TIPOS DE VECTORES:
• A) Vectores colineales
• Son aquellos vectores que están
contenidos en una misma línea
de acción.
r
A
B) Vectores concurrentes
• Son aquellos vectores cuyas líneas
de acción, se cortan en un solo
punto.
C) Vectores coplanares
• Son aquellos vectores que
están contenidos en un
mismo plano.
Dr.Erwin F.Haya E.
r
C
r
B
r
B
0
r
C
r
A
r
B
r
A
r
C

13. D) Igualdad de vectores: r
r
r
r
Sean A y B dos vectores, A = B entonces
si y r
solo si tienen igual magnitud y dirección.
A
r
B
r
a
α
r
B
α
E) Vector opuesto:
r
r
Sea Aun vector. Se llama vector opuesto deA al vector que
r
tiene la misma r
magnitud pero sentido contario que A . Se
designa por − A .
r
−A
r
A
Dr.Erwin F.Haya E.
r
A
r
−A

14. Vector unitario
• Es la unidad vectorial representativa que se
caracteriza por su modulo que siempre es la
unidad.
• Se manifiesta colineal o paralelo al vector. Es
decir tienen la misma dirección y sentido.
r
$ = A Vector ,
u
r
A Modulo
r
A
)
u
Vector unitario
• Cualquier vector puede ser representado como el r
ˆ
producto de un vector unitario a en la dirección de A y
r
la magnitud de A .
O sea:
r
ˆ
A = Aa
Dr.Erwin F.Haya E.

15. Los versores cartesianos
Un vector unitario es un vector sin dimensiones que tiene una magnitud
exactamente igual a uno. Se usan sólo por conveniencia en la descripción
de una dirección en el espacio. Se usan los símbolos i, j y k para
representar vectores unitarios que apuntan en las direcciones x, y y z
respectivamente. Como se muestra en la figura
ˆ
k = (0,0,1)
ˆ
k
O
ˆ
i
x
ˆ
j
ˆ
i = (1,0 ,0)
y
ˆ = (0,1,0)
j

16. Componentes de un vector
• Si se considera un
sistema cartesiano XYZ,
cualquier vector en el
espacio podrá ser
considerado como la suma
de 3 vectores en la
dirección r r que se
X,Y,Z r
llamaran Ax , Ay , Az
respectivamente.
z
r
Az
r
A
Es decir:
r r r r
A = Ax + Ay + Az
r
A = ( Ax , Ay , Az )
r
Ax
x
Dr.Erwin F.Haya E.
(Ax,Ay,Az)
r
Ay
r
Ax
y

17. Es decir:
r r r r
A = Ax + Ay + Az
z
ˆ j ˆ
• Si se llaman i , ˆ , k a los tres
vectores unitarios en las
direcciones X, Y, Z
respectivamente, entonces:
r
ˆ
Ax = Ax i
r
Ay = Ay ˆ
j
r
ˆ
Az = Az k
r
Az
ˆ
k
r
Ax
ˆ
i
r
A
(Ax,Ay,Az)
ˆ
j
r
Ay
x
r
ˆ
A = Ax iˆ + Ay ˆ + Az k
j
r
2
2
2
A = Ax + Ay + Az
Dr.Erwin F.Haya E.
y

18. Cosenos directores
Z
r
Az
γ
r
Ax
o
α
r
A
β
(Ax,Ay,Az)
r
Ay
Y
X
Dr.Erwin F.Haya E.
son los cosenos de los
ángulos α, β y γ que
forma el vector con
los ejes del sistema
de referencia.
r
Ax = A cos α
r
Ay = A cos β
r
Az = A cos γ

19. Componentes de un vector
Z
r
v
(vx,vy,vz)
r vr
vy j zk
Y
r
vx i
O
X
(
Un vector se puede
expresar en función de
sus componentes y de
los vectores unitarios
del sistema de
referencia como la
suma de tres vectores
en las direcciones de
los mismos
r
r
r
r
v = vx i + v y j + vz k
r
r
r
r r
v = v cos αi + cos β j + cos γk
Dr.Erwin F.Haya E.
)

20. Las componentes del vector unitario de un vector
son los cosenos directores del vector (cosα, cosβ,
cosγ)
Z
r
r
r
r
v = vx i + v y j + vz k
r
v
O
r
uv
r
vx = v cos α
r
v y = v cos β
r
vz = v cos γ
(vx,vy,vz)
Y
r
r
r
r r
v = v cos αi + cos β j + cos γk
(
X
)
r
r
r
r
r
v
uv = r = cos αi + cos βj + cos γk
v
Dr.Erwin F.Haya E.

21. →
• Calcular los valores de X que hace que el vector A sea
un vector unitario
(
r
A = x, 1
r
A =1
r
A =
r
A =
2
)
x + (1/ 2)
2
2
x + (1/ 2) = 1 ⇒ x + (1/ 2) = 1
2
2
1 3
3
x =1 − = ⇒ x = ±
4 4
4
2
2
2

22. Metodos analiticos
• Cuando un conjunto de vectores no son coliniales ni
paralelos, cuyos módulos y direcciones son conocidos,
entonces podemos determinar mediante métodos
analíticos:
• Método del triangulo o ley de senos
• Método del paralelogramo o ley de cósenos
• Método de descomposición rectangular.
• Metodo del triangulo o
teorema del seno:
R
A
B
=
=
senβ senδ senα
Dr.Erwin F.Haya E.
r
R
α
r
B
δ
β
r
A

23. • Señale el valor del ángulo que forman dos vectores de 8 y 10
unidades de longitud cuando su resultante forma un ángulo
de 50 grados con el vector mayor.
r
B = 8u
α
r r r
R = A+B
50o
r
A = 10u
r r r
R = A+ B
50o
r
A = 10u
180o − α
α − 50o
r
B = 8u
α
A
B
10u
8u
=
⇒
=
o
o
o
sen(α − 50 ) sen(50 )
sen(α − 50 ) sen50o
10 sen50o
sen(α − 50o ) =
= 0.96 ⇒ α = 123.2o
8

24. • Método del paralelogramo
Se emplea para calcular el módulo de 2 vectores que
forman un angulo entre si.
r r r
R = A+ B
r r
R = A+ B =
r
B
A2 + B 2 + 2 AB cos α
r r r
R = A+ B
α
r
A
Dr.Erwin F.Haya E.

25. • Metodo de descomposicion rectangular
Nos permite determinar el modulo y la dirección de la resultante de
un conjunto de vectores concurrentes y coplanares.
ϕ
F
θ
Re
Q Senθ
β
R
= V
= P cos β − Qsenθ
( x) ∑ ( x)
R
= V
= Psenβ − Q cos θ
( y) ∑ ( y)
F Cosθ
W Cosα
α
Q cosθ
(X)
(X)
θ
W Senα
P cosβ
θ
Q
(Y)
P
n
Se
F
P Senβ
(Y)
W
R
= V
= F cos θ −Wsenα
( x) ∑ ( x)
R
= V
= Fsenθ −W cos α
( y) ∑ ( y)
La resultante se obtienen sumando algebraicamente los vectores
coliniales en cada eje *X* y en*Y*,
Modulo : Re = R( x ) + R( y )
2
2
 R( y )
Direccion : ϕ=Arctg 
R
 (x)

÷
÷


26. TSen45
TT
45
T Cos45
(X)
1mg
T = 1mg
∑ Fy = 0
∑ Fx = 0
Ry = 2T + Tsen45o = T ( 2 + sen 45o )
Rx = T cos 45O = ( 1mg ) ( 0.707 )
Ry = 2.707mg
Rx = 0.707 mg
2
R = Rx2 + Ry =
R = 2.8mg
( 0.707mg ) + ( 2.707mg )
2
2
tan θ =
Ry
Rx
=
2.707
= 3.828 ⇒ θ = 75.3o
0.707

27. Producto punto o escalar entre vectores
• El producto escalar de r los vectores
r
representado por el símbolo A ⋅ B , se define r
r
como el producto de las magnitudes de yA
B
con el coseno del ángulo entre los dos
vectores. Se llama escalar, porque el resultado
por definición es una magnitud escalar.
r
B
θ
r
A
r r
A ⋅ B = AB cos θ
r r r r
A⋅ B = B ⋅ A
Dr.Erwin F.Haya E.

28. r r r r
A⋅ B = B ⋅ A
• De la definición se puede ver que:
ˆ ˆ
i ⋅i =
ˆ j
i⋅ˆ=
Si:
Entonces:
Notese que:
ˆ⋅ ˆ = k ⋅k =1
j j ˆ ˆ
ˆ ⋅ k = k ⋅i = 0
j ˆ ˆ ˆ
r
ˆ
A = Ax iˆ + Ay ˆ + Az k
j
r
ˆ
B = Bx iˆ + B y ˆ + Bz k
j
r r
A ⋅ B = Ax Bx + Ay B y + Az Bz
r r
2
2
2
2
A ⋅ A = Ax + Ay + Az = A
Dr.Erwin F.Haya E.

29. Producto cruz o vectorial entre vectores
r r
• El producto vectorial de dos r r
vectores A y B es
representado por el símbolo A × B , es definido,
como un vector
r r
• La dirección del vector A × B es perpendicular
r r
al plano formado por A y B
(regla de la mano
derecha).
r r
A× B
ˆ
n
r
B
θ
r
A
Dr.Erwin F.Haya E.
r r
A× B
ˆ
n
r
B
θ
r
A

30. r r
A × B = ( ABsenθ )n
ˆ
•
En que n
ˆ es un
vector unitario que
indica la r
dirección de
r
A.× B
r r
A× B
ˆ
n
r r
r r
A× B = −B × A
r
B
θ
r
A
Dr.Erwin F.Haya E.

31. De la definición tenemos:
r r
ˆ
A × B = A B senθ .n
r
ˆ ˆ j j ˆ ˆ
i ×i = ˆ× ˆ = k ×k = 0
ˆ j ˆ
i׈=k
ˆ×k = i
j ˆ ˆ
ˆ ˆ j
k ×i = ˆ
Z
ˆ
k
ˆ
i
Y
ˆ
j
X
r r
r r r r r
r
 i ×i = 0
i × j = k i ×k = − j
r r r
r r
r r
r r
r r r

A × B = A · B sin α  j × i = −k
j× j =0
j ×k = i
r r r
 r r r r r
 k × i = j k × j = −i k × k = 0

Dr.Erwin F.Haya E.

32. r
ˆ
ˆ
Si: A = Ax i + Ay ˆ + Az k
j
r
ˆ
ˆ
B = Bx i + B y ˆ + B z k
j
iˆ ˆ k
j ˆ
r r
A × B = Ax Ay Az =
Bx By Bz
r
r
r
= ( Ay Bz − Az By ) i + ( Az Bx − Ax Bz ) j + ( Ax By − Ay Bx ) k
Dr.Erwin F.Haya E.

33. Vector entre dos puntos
A(ax,ay,az)
r
r
r
OA = a x i + a y j + a z k
Eje z
B(bx,by,bz)
OA
r
r
r
OB = bx i + by j + bz k
OB
Eje y
Eje x
uuu uuu uuu
r
r
r
r
r
r
AB = OB − OA = (bx − a x )i + (by − a y ) j + (bz − a z )k
Dr.Erwin F.Haya E.

34. En la figura se observa un cubo cuya arista es la unidad. Realizar
las siguientes operaciones vectoriales
z
r
B
r
A
y
x

35. r
a
r r
a +b
r
b
suma
r
r
r
r
r
r
r r
a + b = ( a x i + a y j + a z k ) + ( bx i + by j + bz k ) =
r
r
r
= ( a x + bx ) i + ( a y + by ) j + ( a z + bz ) k
producto escalar
r
a
r
r
r
r
r
r
rr
a ·b = ( a x i + a y j + a z k )·( bx i + by j + bz k ) =
α
r r
a ×b
ˆ
n
= ( a x ·bx ) + ( a y ·by ) + ( a z ·bz )
r
b
θ
r
a
producto vectorial
r
b
r
r
r
r
r
r
r r
a × b = ax i + a y j + az k × bx i + by j + bz k =
r r r
i
j k
r
r
r
r
r
a × b = ax a y az = ( a y bz − az by ) i − ( axbz − az bx ) j + ( axby − a ybx ) k
(
) (
bx by bz
Dr.Erwin F.Haya E.
)

36. Calcular el área del paralelogramo (|u x v|)
r
U = iˆ + ˆ + k ≡ (1,1,1)
j ˆ
Si:
r
V = ˆ + k ≡ (0,1,1)
j ˆ
r
V
r
U
ˆ j ˆ
i ˆ k
r r
1 1
1 1 ˆ1 1
ˆ
ˆ
U ×V = 1 1 1 = i
−j
+k
1 1
0 1
0 1
0 1 1
r
r
r
r
r
r
= ( 1.1 − 1.1) i + ( 1.1 − 1.0 ) j + ( 1.1 − 1.0 ) k = ( 0 ) i + ( 1) j + ( 1) k
r r r
r r
r
⇒ U × V = ( 1) j + ( 1) k ≡ j + k
r r
el modulo del producto vectorial U × V = 02 + 12 + 12 = 2
r r
∴ U × V = 2 u 2 Nos define el area del paralelogramo
Dr.Erwin F.Haya E.

37. Calcular el área del paralelogramo (|u x v|)
r
ˆ
ˆ
U = (2, − 0) ≡ 2i −1 ˆ +0k
1,
j
r
ˆ
ˆ
V = ( −1, 2, 0) ≡ −1i + 2 ˆ + 0k
j
Si:
ˆ
i
r r
U ×V = 2
−1
ˆ
j
ˆ
k
ˆ
−1 0 = i
2
0
-1 0
2 0
−ˆ
j
r
V
r
U
2 0
ˆ 2 -1
+k
-1 0
-1 2
r
r
r
= ( (−1).0 − 2.0 ) i − ( 2.0 − 0.(−1) ) j + ( 2.2 − (−1)( −1) ) k
r
r
r
= ( 0 ) i + ( 0 ) j + ( 3) k
r
r
r r
r
r
⇒ U × V = 0.i + 0. j + 3.k ≡ 3k
r r
el modulo del producto vectorial U ×V = 0 2 + 0 2 + 32 = 3
r r
2
∴ U × V = 3 u Nos define el area del paralelogramo
Dr.Erwin F.Haya E.

38. Calcular el área del triángulo con los vértices dados. (Sugerencia:
(1/2)|u x v| es el área del triángulo que tiene u y v como lados
adyacentes) (1,2,0), (-2,1,0), (0,0,0)
Definimos los vectores U y V
r
U = (1, 2, 0) −(0, 0, 0) = (1, 2, 0)
r
⇒ U = (1, 2, 0)
r
V = (−2,1, 0) − (0, 0, 0) = ( −2,1, 0)
r
⇒ V = (−2,1, 0)
(−
2,1, 0)
r
V
(0, 0, 0)
1 r r
A = UxV
2
A
r
U
(1, 2, 0)
Dr.Erwin F.Haya E.
Ell Area es igual al producto
vectorial de dos vectores
dividido por dos

39. r
ˆ
ˆ
U = (1, 2, 0) ≡1i +2 ˆ +0 k
j
r
ˆ
ˆ
V = ( −2,1, 0) ≡ −2i +1 ˆ + 0k
j
Si:
ˆ
i
r r
U ×V = 1
−2
ˆ
j
ˆ
k
2
ˆ
0 =i
1 0
2 0
1 0
−ˆ
j
1 0
ˆ1 2
+k
-2 0
-2 1
r
r
r
= ( 2.0 − 0.1) i − ( 1.0 − 0.(−2) ) j + ( 1.1 − (2)( −2) ) k
r
r
r
= ( 0 ) i + ( 0 ) j + ( 5) k
r
r
r r
r
r
⇒ U × V = 0.i + 0. j + 5.k ≡ 5k
r r
el modulo del producto vectorial U ×V = 0 2 + 0 2 + 52 = 5
1 r r 1 2
∴ A = UxV = 5 u =2.5u 2 Nos define el area del triangulo
Dr.Erwin F.Haya E.
2
2

40. (0, k , k )
(0,0,0)
B) Hallar el ángulo entre cada
dos aristas.
k k k
( , , )
2 2 2
(k ,0, k )
θ
(k , k ,0)
Considerar un tetraedro
regular con los vértices
(0,0,0), (k,k,0), (k,0,k) y
(0,k,k), donde k es un
numero real positivo.
A) Hallar la longitud de cada
arista.
Dr.Erwin F.Haya E.
C) Hallar el ángulo entre los
segmentos de recta desde
el centroide (k/2,k/2,k/2)
a dos de los vértices.

41. r
A = ( x, y, z ) = ( k − k , 0 − k , k − 0)
r
A = (0, − k , k )
r
B = ( x, y, z ) = (0 − k , k − k , k − 0)
(0, k , k )
r
B = (− k , 0, k )
(0,0,0)
r r
A ×B = ( 0, − k , k ) ( − k ,0, k ) = k 2
k k k
( , , )
2 2 2
r
B
(k ,0, k )
θ
(k , k ,0)
r
A
Dr.Erwin F.Haya E.
r
A=k 2
r r
A ×B
cos θ = r r =
A B k
r
B =k 2
k2
1
=
2 k 2 2
1
cos θ = ⇒ θ =60o
2

42. CH4
(0, k , k )
(0,0,0)
k k k
( , , )
2 2 2
PbCl4
(k ,0, k )
(k , k ,0)
Dr.Erwin F.Haya E.

43. Para presentar
1. Un avión está viajando a una altura fija y sin la influencia
del aire. El avión viaja a una velocidad de 500km/h, con un
ángulo de 120° como muestra la figura (a). Cuando el avión
alcanza un cierto punto, el aire influye con una velocidad de
70 km/h en la dirección 45° NE como se muestra en la
figura (b). ¿Cuál es la velocidad resultante y su dirección

44. 2. Una pared de concreto está temporalmente en posición
vertical sujetada por cuerdas como muestra la figura.
Encontrar la fuerza total ejercida sobre la estaca en la
posición A. Las tensiones en las cuerdas AB y AC son 190 kg
y 300 kg.
3. Una cámara de TV tiene una mas de 25 kg y es sostenida
por un trípode, como se muestra en la figura. Representar la
fuerza ejercida en cada “pata” del trípode como un vector.