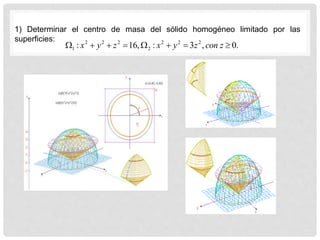
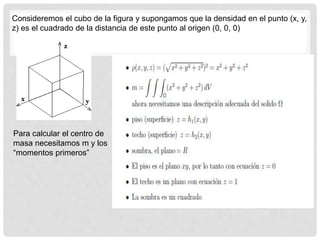
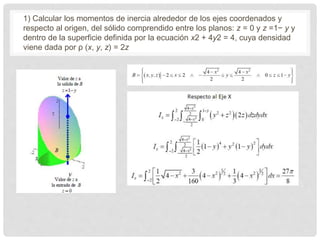
Este documento presenta información sobre integrales triples y su aplicación para calcular volúmenes y masas. Incluye definiciones de integral triple, utilidad de las integrales triples para calcular volúmenes de figuras geométricas, y ejemplos de cálculo de masa y centro de masa usando integrales triples. También cubre conceptos como momento de inercia y cómo usar integrales triples para calcularlos.

1. E S T U D I A N T E S :
B E N I T E S A L A R C Ó N , M A N U E L
V I LC H E Z P E R E Z , J O E L
M A N R I Q U E G U Z M Á N , J H O N
LÓ P E Z R A M Í R E Z , R O D M Y
APLICACIÓN DE LAS
INTEGRALES TRIPLES

2. DEFINICIÓN DE INTEGRAL TRIPLE
INTEGRAL TRIPLE:
Es la aplicación sucesiva de tres procesos de integración definida simple a una
función de tres variables f (x, y, z); tomando en consideración en función de que
variable se encuentran los límites para saber cual diferencial (dx, dy, dz) se
utilizará primero y cual después y cual al final.
UTILIDAD DE LAS INTEGRALES TRIPLES:
Generalmente se utilizan para el cálculo de volúmenes de curvas espaciales
cerradas o de cuerpos espaciales tales como esferas, elipsoides, cubos,
tetraedros o combinaciones de estas superficies.

3. VOLUMEN
Es una magnitud escalar definida como el espacio
ocupado por un cuerpo. Es una función derivada ya que
se halla multiplicando las tres dimensiones.

4. •

5. •

6. •

7. •

8. MASA
La masa, es la cantidad de materia de un cuerpo. Es una propiedad
intrínseca de los cuerpos que determina la medida de la masa inercial
y de la masa gravitacional. La unidad utilizada para medir la masa en
el Sistema Internacional de Unidades es el kilogramo (kg). Es una
cantidad escalar y no debe confundirse con el peso, que es una
cantidad vectorial que representa una fuerza.

9. Grafica solucion
• El sólido B se muestra en
la figura, también se
muestran los valores que
toma la variable z a la
entrada y salida de la
región B.
CALCULAR LA MASA DEL SÓLIDO COMPRENDIDO ENTRE LOS PLANOS: Z = 0 Y
Z =1− Y Y DENTRO DE LA SUPERFICIE DEFINIDA POR LA ECUACIÓN
X2 + 4Y2 = 4 , CUYA DENSIDAD VIENE DADA POR Ρ (X, Y, Z) = 2Z

10. PROYECCION

11. 2.CALCULAR LA MASA DEL SOLIDO COMPRENDIDO ENTRE LOS
PARABOLOIDES ,CUYA DENSIDAD VIENE
DADA POR
• En la figura, se muestra
el sólido B y también
los valores que toma la
variable z a la entrada y
salida de la región B,
los cuales permiten
establecer los límites
para la primera
integración parcial.
•

12. SOLUCIÓN
• Por lo tanto, la masa
se obtiene como:
• sistema, se obtiene la
ecuación de la
circunferencia y
puede ser tipo I oII
•
Siendo D la proyección del sólido B en el
plano xy. Para determinar la ecuación de
la curva que delimita a esta región D, es
necesario resolver el siguiente sistema:
Sumando ambas ecuaciones se tiene que
z = 4

13. La region de queda definida como:
Luego la masa se obtiene:

14. 3.DETERMINE LA MASA DE UN CUBO, DADO QUE LA DENSIDAD EN
EL PUNTO (X,Y,Z) ES PROPORCIONAL AL CUADRADO DE LA
DISTANCIA DE SU ORIGEN.

15. •
•

16. CENTRO DE MASA
• El centro de masas de un sistema discreto o continuo es el punto
geométrico que dinámicamente se comporta como si en él estuviera
aplicada la resultante de las fuerzas externas al sistema. De manera
análoga, se puede decir que el sistema formado por toda la masa
concentrada en el centro de masas es un sistema equivalente al
original.

17. 1) Determinar el centro de masa del sólido homogéneo limitado por las
superficies:
.
0
,
3
:
,
16
: 2
2
2
2
2
2
2
1 






 z
con
z
y
x
z
y
x

18. Observamos que se trata del cuerpo acotado inferiormente por el cono
2
2
2
2 3
: z
y
x 

 y superiormente por la esfera 16
: 2
2
2
1 


 z
y
x
Por la simetría del problema, sabemos que la abscisa y la ordenada del centro
de masa son 0; que la función que nos da la densidad del cuerpo es con k
una constante positiva, ya que el sólido es
homogéneo. Puede aprovecharse o no la simetría del sólido para hacer los
cálculos (en la figura se ha representado el haber extraído la parte contenida en
el primer octante). Las superficies se intersectan a la altura z = 2, en el cilindro
k
z
y
x
g 
)
,
,
(
12
2
2

 y
x
.
Solución:
Se plantea la siguiente integral triple para el cálculo de la masa del sólido:
  






 
















12
0
12
0
16
3
1
2 2
2
2
2
4
x
x
y
y
x
y
x
z
dx
dy
kdz
M

19. Para las coordenadas del centro de masa  
m
m
m z
y
x
C ,
,
se requieren además:
  









 
















12
12
12
12
16
3
1
2
2
2
2
2
2
x
x
x
y
y
x
y
x
z
x dx
dy
kxdz
M
  









 
















12
12
12
12
16
3
1
2
2
2
2
2
2
x
x
x
y
y
x
y
x
z
y dx
dy
kydz
M
  









 
















12
12
12
12
16
3
1
2
2
2
2
2
2
x
x
x
y
y
x
y
x
z
z dx
dy
kzdz
M

20. Para obtener entonces las coordenadas pedidas mediante:
M
M
x x
m 
M
M
y
y
m 
M
M
z z
m 
Resultados:
k
M
9
)
3
3
(
128 


0

 y
x M
M k
M z
3
128

Las coordenadas del centroide son entonces:
..
366
.
2
3
3
3
,
0 



 m
m
m z
y
x

21. Consideremos el cubo de la figura y supongamos que la densidad en el punto (x, y,
z) es el cuadrado de la distancia de este punto al origen (0, 0, 0)
Para calcular el centro de
masa necesitamos m y los
“momentos primeros”

22. Por lo tanto:

23. Para calcular X necesitamos conocer:
Por lo tanto . Del mismo modo se puede comprobar que
Por lo tanto, el centro de masa es el punto

24. MOMENTO DE INERCIA
• El momento de inercia es una medida de la inercia rotacional de
un cuerpo. Cuando un cuerpo gira en torno a uno de los ejes
principales de inercia, la inercia rotacional puede ser representada
como una magnitud escalar llamada momento de inercia.

25. 1) Calcular los momentos de inercia alrededor de los ejes coordenados y
respecto al origen, del sólido comprendido entre los planos: z = 0 y z =1− y y
dentro de la superficie definida por la ecuación x2 + 4y2 = 4, cuya densidad
viene dada por ρ (x, y, z) = 2z

28. 2) Calcular el momento de inercia de un sólido en forma de cono circular
recto con densidad constante respecto a su eje; Supongamos que el cono de
altura h y radio en la base r tiene vértice en el origen y eje vertical. Entonces
su ecuación es:
Si la densidad en cada punto del sólido es k, el momento de inercia respecto al
eje Z viene dada por la formula:
Para resolver la integral, escribimos el solido en coordenadas cilíndricas, x = u
cos v, y =u sen v. La ecuación del cono se escribe entonces como z = hu/r y la
integral pedida.

29. 3) Hallar los momentos de inercia con respecto alos ejes X y Y de la región
solida comprendida entre el hemisferio.
Y en el plano xy dado que la densidad en (x, y, z) es proporcional ala distancia
entre (x, y, z) y en el plano xy
SOLUCIÓN
La densidad de la región esta dada por
p(x, y, z)=kz. Considerando la simetría de
este problema.se sabe que Ix=Iy, y solo se
necesita calcular un momento digamos, Ix.
De acuerdo ala figura. Se elige el orden
dzdydx y se escribe.